組物
四つの三角リングの組み物 の完成させ方についてお伝えします。
下画像の 左が
三角リングを三っつ組み合わせた状態です。
この状態で あと三本の棒を挿入し
丸棒を斜めにカットした 楕円形の面をピッタリ三か所合わせれば
右のような状態になります。
言うはやすしで 私もその都度頭が混乱してしまいます。
この画像は 一つのタイプの状態で
三角リングを三っつ組み合わせた状態が 二種類あり
この画像を 鏡で左右をひっくり返して見た状態もあります。
こつとしては
三角リングのかどが 三つ組み合わされた状態で上向きにし
あと一つの三角が水平におさまっている
と 考えるとうまくいきました。
でも 完成見本を見ながらでないと
私はなかなか うまくいきません。
すばやく やつてみたいのですが。
この組物の材質は 竹ばしで
三本 横に並べて 17ミリ強の寸法 長さは53.5ミリほどです。

あることで 今日入院して 検査開始を待っています。 ( コロナ関連では幸いありません)
pcr 検査を受けました。唾液採取でした。結果はまだですが陰性のはずです。
退屈しのぎのために 組み方を考えるのもいいかな と持ってきたのを
ベッドのそばに射す 夕日の明りで撮りました。
2020年6月16日
05[3,4,3,4] BASIC 組物
四つの三角リングの組み物について 部品寸法計算も含めて お伝えします。
すでに 製作方法を説明していますので 組物 のカテゴリーをクリックしてもらうと今回の説明と一緒に表示され確認ができます。
[3,4,3,4] Cuboctahedron 立方8面体の頂点と 組物の三角のかどの位置が 合同になります。
[3,4,3,4] は準正多面体なので 頂点から中芯までの寸法 ( 頂芯寸 ) は 一種類です。
しかも稜寸と同じです。
このことから
三角形と中芯点とでどきる三角錐は 正四面体であり
四角形と中芯点とでできる四角錐は 正八面体を二つにカットした形状です。
下画像右でその状態が確認できます。

二種類の二面角の合計は 誤差なしの 180度 つまり平面になります。
[3,3,3] 二面角 70.528779365509308631 ( 198/070 )
[3,3,3,3]二面角 109.47122063449069137 ( 198/070 )
平面の上に 3,4,3,4,3,4 と交互に三つづつ角錐を組合せて置き 上に三角錐の正四面体を載せると 稜線と中芯を含む平面上で立体の半分を形成することができます。
この平面は 正六角形であり この立体では 四方向に平面分割が考えられます。
四つの三角リングの組み物を 太さのない棒 つまり線で構成するとすれば 三角形は この六角形の面に接し 三角のかど点が飛び飛びに六角形のかどに接しています。
この飛び飛びの決定に二つの方法があり それによって 鏡面対称の立体ができます。
この線が太さのある棒であるとしても棒の外周線は面に接し 中芯方向に大きくなってゆき ある太さになれば 上下に離れて交差している棒が 接することになります。
以上の条件を考慮して
以下のプログラムで棒の外周寸と太さの関係を計算しています。
計算結果は 棒の太さを 1 とすると
外周寸は 9.13648175207322 となるということです。
これを 整数比に直し グラフ用紙にその比例関係をプロットすれば どの太さの棒に対しても 外周寸が把握できます。
10本の棒の太さの合計と外周寸との 近似の整数比は 139 対 127 になります。
1本でなく 10本での値を用いているのは 寸法の測定精度が高まるためです。
! コピー開始
! フリーウエアー 十進BASIC でプログラム
! http://hp.vector.co.jp/authors/VA008683/ を参照
! http://hp.vector.co.jp/authors/VA008683/english/index.htm 英語版
! 三角リングの組物の円柱の太さと外周寸の計算
OPTION ANGLE DEGREES
! 三角錐の稜寸は 1 とする
! 故に三角リングの一辺は √3 となる
LET a001=SQR(8)/3 ! .942809041582063 またぎズレ角のコサイン値
LET a002=ATN(TAN(30)*a001) ! 28.5608252178112 三角リングの辺を垂直とする
! 面上のまたぎ角/2
LET a003=SIN(a002)*.5 ! .239045721866878 円柱の太さを 0 にしたときの
! 交差巾
LET a004=a003/3 ! 7.96819072889593E-2 円柱半径初期値
10
LET a005=a004+.5 ! .579681907288959 → .594787624742743
LET a006=SIN(a002)*a005 ! .277140959962116 → .28436287422823
LET a007=a004*3 ! .239045721866878 → .28436287422823
LET a008=a006-a007 ! .038095238095238 → 0
IF a008 > 0 THEN
LET a004=a006/3
GOTO 10
END IF
PRINT "円柱の直径を 1 としたときの三角リングの外周辺寸"
PRINT 1/(a004/SQR(3)*2) ! 9.13648175207322
END
! コピー終わり
追伸
ある国を経由して複数の PCから 一日に何百ものスパムが届きました。
意図が理解できず 驚きと戸惑い を感じています。
ブログへの コメントに対する アクセス機能を制限しましたが
まだ そこからのアクセス数や 閲覧数には 異常な状態が続いています。
2013年10月27日
05[3,4,3,4] Compounds 多面体 組物

[3,4,3,4] の複合多面体 compounds についてお伝えする前に その前提となる
Cuboctahedron 立方8面体と
その双対の Rhombic Dodecahedron 菱形12面体の諸量をまとめて表示しておきます。
この二つの製作方法については 既にお伝えしています。
05 [3,4,3,4] Cuboctahedron 立方8面体
05 .86602540378443864676 [3,4,3,4]基本数
05 30.000000000000000000 [3,4,3,4]仰角( 112/194 )
05 1.0000000000000000000 [3,4,3,4]頂芯寸( 180/180 )
05 .86602540378443864676 [3,4,3,4]稜芯寸( 168/194 )
05 54.735610317245345685 [3,4,3,4]4 接合角( 239/169 )
05 35.264389682754654315 [3,4,3,4]3 接合角( 169/239 )
05 .81649658092772603273 [3,4,3,4]3 面芯寸( 178/218 )
05 .70710678118654752440 [3,4,3,4]4 面芯寸( 169/239 )
05 9.4641016151377545871 [3,4,3,4]面積
05 2.3570226039551584147 [3,4,3,4]体積
05 54.735610317245345685 [3,4,3,4]4 面角( 239/169 )
05 70.528779365509308631 [3,4,3,4]3 面角( 198/070 )
05 125.26438968275465432 [3,4,3,4]二面角
05 [3,4,3,4] 稜部品 必要個数 24
05 双[3,4,3,4] Rhombic Dodecahedron 菱形12面体
05 120.00000000000000000 双[3,4,3,4]二面角
05 .75000000000000000000 双[3,4,3,4]面芯寸( 180/240 )
05 35.264389682754654315 双[3,4,3,4]4 仰角( 169/239 )
05 19.471220634490691369 双[3,4,3,4]3 仰角( 070/198 )
05 .61237243569579452455 双[3,4,3,4]4 稜寸( 109/178 )
05 .30618621784789726227 双[3,4,3,4]3 稜寸( 064/209 )
05 70.528779365509308631 双[3,4,3,4]4 かど角
05 109.47122063449069137 双[3,4,3,4]3 かど角
05 1.0606601717798212866 双[3,4,3,4]4 頂芯寸( 175/165 )
05 .91855865354369178682 双[3,4,3,4]3 頂芯寸( 124/135 )
05 9.5459415460183915794 双[3,4,3,4]面積
05 2.3864853865045978949 双[3,4,3,4]体積
05 45.000000000000000000 双[3,4,3,4]4 接合角/2( 180/180 )
05 60.000000000000000000 双[3,4,3,4]3 接合角/2( 194/112 )
05 .91855865354369178682 双[3,4,3,4]稜寸( 124/135 )
05 1.2247448713915890491 双[3,4,3,4]稜寸/面芯寸( 218/178 )
05 双[3,4,3,4] 稜部品 必要個数 24
05 [3,4,3,4]compounds 複合多面体 作成に必要な諸量
05 .57735026918962576451 複[3,4,3,4]0.5/稜芯寸( 112/194 )
05 .35355339059327376220 複[3,4,3,4]3形 稜寸/稜芯寸( 070/198 )
05 .70710678118654752440 複[3,4,3,4]4形 稜寸/稜芯寸( 169/239 )
05 [3,4,3,4]3,4形稜部品 必要個数 24
05 [3,4,3,4]3,4形と鏡面対称な稜部品 必要個数 24
05 双[3,4,3,4]4形稜部品 必要個数 24
05 双[3,4,3,4]3形稜部品 必要個数 24
2013年2月5日
05[3,4,3,4] 多面体 組物 製作道具
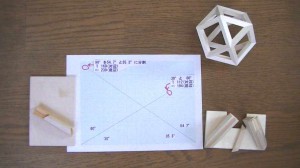
“三角の組み物” と兄弟関係にある立方八面体の 製作関連写真です。
この多面体は 製作2 製作3 でお伝えした 二十・十二面体と同じく
一つの形状の部品で組み立てられ 三角形に組んだ部品の結合でできます。
クレィドルも 傾斜は一つの角度 ( 30°)で
余角の 60°でカットした面を垂直にした部品を
二種類の接合角 (54.7°と35.3°計 90°) になるよう整形し
部品の両端の形状を 二十・十二面体と同じく面対称にして 24個が必要です。
“三角の組み物”と立方八面体が 兄弟関係にあると説明しましたが
組み物や多面体の頂点の位置が 合同になることができ
組み物の部品の太さと長さの比の値を この立方八面体から計算できるからです。
計算方法は説明困難ですが
多面体の三角形の面と中芯点とでできる立体は “正四面体” で
組み物の外周線は正四面体の面に斜めに “接して” います。
これらを条件として計算をしています。
私は 立方八面体を [ 3,4,3,4 ] (さんよん さんよん)と 呼んでいます。
多面体の一つの頂 (ちょう) に集まる多角形の状態を表しています。
形状が判り すっきりしている気がします。
複数の正多角形でできている準正多面体 の名称は
形状を確定するプロセスや いきさつが解かっていないと
意味不明な部分が多く 馴染みにくい気がします。
正四面体は [ 3,3,3 ](さんみっつ) 正六面体は [ 4,4,4 ] (よんみっつ)。
正八面体は [ 3,3,3,3 ] (さんよっつ)正十二面体は [ 5,5,5 ] (ご みっつ)。
正二十面体は [ 3,3,3,3,3 ] (さんいつつ)とも表現できます。
これらはどれも 正多角形が一種類でできていて 正多面体と呼ばれています。
今までにお伝えした 複数の正多角形でてきた準正多面体 は以下です。
二十・十二面体は [ 3,5,3,5 ]
サッカーボールは [ 5,6,6 ]で 切頂二十面体や
フラーレン fullerene とも呼ばれています。
2012年7月2日
組物 製作道具

これが四つの三角リングの組み物の 製作基本図です いたってシンプルです。
この組み物を作る場合必要な条件は 円柱棒の直径が 1 に対し 円柱で作る正三角形の
外周の一辺が 9.1364817520732 (私の計算では) でなければなりません。
それより小さければ 組み合わず 大きすぎれば 組み合わせがゆるんで形状が保てません。
今回 製作見本として 直径 12mmと表示された バルサ材の棒を用いていますが
10本横に並べて寸法を計測すると 123mm でした。
実際の直径は 平均 12.3mm ということです。

写真に 三角形を二個組み合わせたのが二つありますが
面対象に 二種類の組み方があることがわかります。
どちらかの二個組み合わせてできた輪の中に 三番目の三角形の輪を作ります。
これで三個の三角形の組み物ができあがりました。
つぎは 残る三つのパーツを できた組み合わせの中にシィメトリーに挿入すれば
出来上がりです。
その作業はパズルのようで 説明困難です。
部品が正確にできていれば 最後の三つの部品は接着せずとも全体の形状を保ちます。
これは実際に パズルとして遊べます
2012年6月30日
04[3,3,3,3,3] 09[5,5,5] Compounds 多面体 組物 製作道具
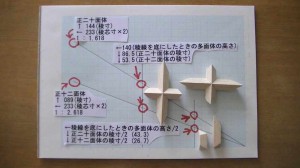
正十二面体と正二十面体との複合多面体 compounds 製作の
基本図面と その部品です。
二つの多面体を複合するには
稜から中芯点までの寸法が同じであることが必要です。
今回寸法を統一して 高さを 140mm とします。

部品の結合作業中です。

完成です この複合多面体は私にとって プロトタイプです。
すす竹では 作ろうという元気が起こりませんでした。

次回は 四つの三角リングでつくる シィメトリーな組み物を お伝えします。
準正多面体 の立法八面体とは兄弟関係にあります。
この組み物はよく目にするのですが どう呼ばれているのか知りません。
2012年6月25日













