RECENT POSTS
『年が変わってからは 今までとは違った表現で
動画もふくめて 発表してゆこうと心に決めています。』
と 年末の挨拶を閉めたものの 番外での お茶濁しばかりでしたが
新しい動きをお知らせします。
私の近しい身内の女性が
私の製作グッズをメルカリで 発表してくれました。
私はノータッチで すべて彼女に全権委任です。
以下のような表現で 出品しています。
どうぞ 御ひいきの程 よろしくおねがいします。
polyhedron
ブログに掲載している多面体関連グッズを販売しています
多面体模型の製作方法などはブログをご確認ください
模型は接合面が小さいですので衝撃が加わると破損します
製作後自宅保管しているものなので経年による材の色むらなどが起こっていることがあります
手作業による誤差、ボンド汚れなどもあります
上記のことにご了解いただいたうえで
ご検討ください
ブログ多面体
http://luckylife.sakura.ne.jp/polyhedron/
2022年5月30日
ことばに出すことと 現実に形にするということの大きな違いを実感する今日このごろです。
テーマとして少し的外れかもしれない話題ですが 番外としてひとつ。
以前
数独 初級 攻略 プログラム のエピソードで お伝えしたことの続編です。
「Excel では IF文が錯綜し 頭が混乱しました」と言っていましたが
今回 それをシンプルにすることができました。
「なんだそんなことか」と思われるようなことも言葉や文章で表すのは苦手です。
形にできたものとして お伝えします。
表現のロジックとしては シンプルです。
数字を決定する場所は 横３マス縦３マスの９マスの枠組みを横３個 縦３個
一つのマスの数字はそのマスを含む 縦列９個 横列９個 枠内の９個内の
他と異なる数だということです。詳しくは アマタある関連書等々を参照してください。
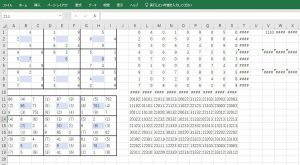
エクセルの A１に全範囲をペイストしてください。
画像を整える必要がありますが 下画像を参考にしてください。
A１から I９の範囲のマスが入力するところです。説明は不要でしょう。
="" =4 ="" =1 ="" =9 ="" =5 ="" ="" =IF(A1="",0,A1) =IF(B1="",0,B1) =IF(C1="",0,C1) =IF(D1="",0,D1) =IF(E1="",0,E1) =IF(F1="",0,F1) =IF(G1="",0,G1) =IF(H1="",0,H1) =IF(I1="",0,I1) =INT((10^K1+10^L1+10^M1+10^N1+10^O1+10^P1+10^Q1+10^R1+10^S1)/10) ="" =INT((10^K1+10^L1+10^M1+10^K2+10^L2+10^M2+10^K3+10^L3+10^M3)/10) =INT((10^N1+10^O1+10^P1+10^N2+10^O2+10^P2+10^N3+10^O3+10^P3)/10) =INT((10^Q1+10^R1+10^S1+10^Q2+10^R2+10^S2+10^Q3+10^R3+10^S3)/10) =2 ="" ="" =5 ="" =3 =8 ="" =4 ="" =IF(A2="",0,A2) =IF(B2="",0,B2) =IF(C2="",0,C2) =IF(D2="",0,D2) =IF(E2="",0,E2) =IF(F2="",0,F2) =IF(G2="",0,G2) =IF(H2="",0,H2) =IF(I2="",0,I2) =INT((10^K2+10^L2+10^M2+10^N2+10^O2+10^P2+10^Q2+10^R2+10^S2)/10) ="" ="" ="" ="" ="" =3 ="" =6 =2 =4 ="" =9 ="" ="" =IF(A3="",0,A3) =IF(B3="",0,B3) =IF(C3="",0,C3) =IF(D3="",0,D3) =IF(E3="",0,E3) =IF(F3="",0,F3) =IF(G3="",0,G3) =IF(H3="",0,H3) =IF(I3="",0,I3) =INT((10^K3+10^L3+10^M3+10^N3+10^O3+10^P3+10^Q3+10^R3+10^S3)/10) ="" ="" ="" ="" =4 ="" =6 =9 =3 =7 =5 ="" =1 ="" =IF(A4="",0,A4) =IF(B4="",0,B4) =IF(C4="",0,C4) =IF(D4="",0,D4) =IF(E4="",0,E4) =IF(F4="",0,F4) =IF(G4="",0,G4) =IF(H4="",0,H4) =IF(I4="",0,I4) =INT((10^K4+10^L4+10^M4+10^N4+10^O4+10^P4+10^Q4+10^R4+10^S4)/10) ="" =INT((10^K4+10^L4+10^M4+10^K5+10^L5+10^M5+10^K6+10^L6+10^M6)/10) =INT((10^N4+10^O4+10^P4+10^N5+10^O5+10^P5+10^N6+10^O6+10^P6)/10) =INT((10^Q4+10^R4+10^S4+10^Q5+10^R5+10^S5+10^Q6+10^R6+10^S6)/10) =5 =7 ="" ="" =6 ="" ="" =8 =3 ="" =IF(A5="",0,A5) =IF(B5="",0,B5) =IF(C5="",0,C5) =IF(D5="",0,D5) =IF(E5="",0,E5) =IF(F5="",0,F5) =IF(G5="",0,G5) =IF(H5="",0,H5) =IF(I5="",0,I5) =INT((10^K5+10^L5+10^M5+10^N5+10^O5+10^P5+10^Q5+10^R5+10^S5)/10) ="" ="" ="" ="" ="" =1 =9 ="" ="" ="" =7 =4 ="" ="" =IF(A6="",0,A6) =IF(B6="",0,B6) =IF(C6="",0,C6) =IF(D6="",0,D6) =IF(E6="",0,E6) =IF(F6="",0,F6) =IF(G6="",0,G6) =IF(H6="",0,H6) =IF(I6="",0,I6) =INT((10^K6+10^L6+10^M6+10^N6+10^O6+10^P6+10^Q6+10^R6+10^S6)/10) ="" ="" ="" ="" =9 =2 ="" =7 ="" =8 ="" =3 =5 ="" =IF(A7="",0,A7) =IF(B7="",0,B7) =IF(C7="",0,C7) =IF(D7="",0,D7) =IF(E7="",0,E7) =IF(F7="",0,F7) =IF(G7="",0,G7) =IF(H7="",0,H7) =IF(I7="",0,I7) =INT((10^K7+10^L7+10^M7+10^N7+10^O7+10^P7+10^Q7+10^R7+10^S7)/10) ="" =INT((10^K7+10^L7+10^M7+10^K8+10^L8+10^M8+10^K9+10^L9+10^M9)/10) =INT((10^N7+10^O7+10^P7+10^N8+10^O8+10^P8+10^N9+10^O9+10^P9)/10) =INT((10^Q7+10^R7+10^S7+10^Q8+10^R8+10^S8+10^Q9+10^R9+10^S9)/10) =1 ="" =3 =2 ="" =5 =4 ="" =8 ="" =IF(A8="",0,A8) =IF(B8="",0,B8) =IF(C8="",0,C8) =IF(D8="",0,D8) =IF(E8="",0,E8) =IF(F8="",0,F8) =IF(G8="",0,G8) =IF(H8="",0,H8) =IF(I8="",0,I8) =INT((10^K8+10^L8+10^M8+10^N8+10^O8+10^P8+10^Q8+10^R8+10^S8)/10) ="" ="" ="" ="" =7 ="" =8 =3 ="" =6 =2 ="" =9 ="" =IF(A9="",0,A9) =IF(B9="",0,B9) =IF(C9="",0,C9) =IF(D9="",0,D9) =IF(E9="",0,E9) =IF(F9="",0,F9) =IF(G9="",0,G9) =IF(H9="",0,H9) =IF(I9="",0,I9) =INT((10^K9+10^L9+10^M9+10^N9+10^O9+10^P9+10^Q9+10^R9+10^S9)/10) ="" ="" =987654321 ="" ="" ="" ="" ="" ="" ="" ="" ="" ="" ="" =INT((10^K1+10^K2+10^K3+10^K4+10^K5+10^K6+10^K7+10^K8+10^K9)/10) =INT((10^L1+10^L2+10^L3+10^L4+10^L5+10^L6+10^L7+10^L8+10^L9)/10) =INT((10^M1+10^M2+10^M3+10^M4+10^M5+10^M6+10^M7+10^M8+10^M9)/10) =INT((10^N1+10^N2+10^N3+10^N4+10^N5+10^N6+10^N7+10^N8+10^N9)/10) =INT((10^O1+10^O2+10^O3+10^O4+10^O5+10^O6+10^O7+10^O8+10^O9)/10) =INT((10^P1+10^P2+10^P3+10^P4+10^P5+10^P6+10^P7+10^P8+10^P9)/10) =INT((10^Q1+10^Q2+10^Q3+10^Q4+10^Q5+10^Q6+10^Q7+10^Q8+10^Q9)/10) =INT((10^R1+10^R2+10^R3+10^R4+10^R5+10^R6+10^R7+10^R8+10^R9)/10) =INT((10^S1+10^S2+10^S3+10^S4+10^S5+10^S6+10^S7+10^S8+10^S9)/10) ="" ="" ="" =V1+W1+X1+V4+W4+X4+V7+W7+X7 ="" =IF(A1="",(IF(MID(K11,1,1)="0",9,"")&IF(MID(K11,2,1)="0",8,"")&IF(MID(K11,3,1)="0",7,"")&IF(MID(K11,4,1)="0",6,"")&IF(MID(K11,5,1)="0",5,"")&IF(MID(K11,6,1)="0",4,"")&IF(MID(K11,7,1)="0",3,"")&IF(MID(K11,8,1)="0",2,"")&IF(MID(K11,9,1)="0",1,"")),("("&A1&")")) =IF(B1="",(IF(MID(L11,1,1)="0",9,"")&IF(MID(L11,2,1)="0",8,"")&IF(MID(L11,3,1)="0",7,"")&IF(MID(L11,4,1)="0",6,"")&IF(MID(L11,5,1)="0",5,"")&IF(MID(L11,6,1)="0",4,"")&IF(MID(L11,7,1)="0",3,"")&IF(MID(L11,8,1)="0",2,"")&IF(MID(L11,9,1)="0",1,"")),("("&B1&")")) =IF(C1="",(IF(MID(M11,1,1)="0",9,"")&IF(MID(M11,2,1)="0",8,"")&IF(MID(M11,3,1)="0",7,"")&IF(MID(M11,4,1)="0",6,"")&IF(MID(M11,5,1)="0",5,"")&IF(MID(M11,6,1)="0",4,"")&IF(MID(M11,7,1)="0",3,"")&IF(MID(M11,8,1)="0",2,"")&IF(MID(M11,9,1)="0",1,"")),("("&C1&")")) =IF(D1="",(IF(MID(N11,1,1)="0",9,"")&IF(MID(N11,2,1)="0",8,"")&IF(MID(N11,3,1)="0",7,"")&IF(MID(N11,4,1)="0",6,"")&IF(MID(N11,5,1)="0",5,"")&IF(MID(N11,6,1)="0",4,"")&IF(MID(N11,7,1)="0",3,"")&IF(MID(N11,8,1)="0",2,"")&IF(MID(N11,9,1)="0",1,"")),("("&D1&")")) =IF(E1="",(IF(MID(O11,1,1)="0",9,"")&IF(MID(O11,2,1)="0",8,"")&IF(MID(O11,3,1)="0",7,"")&IF(MID(O11,4,1)="0",6,"")&IF(MID(O11,5,1)="0",5,"")&IF(MID(O11,6,1)="0",4,"")&IF(MID(O11,7,1)="0",3,"")&IF(MID(O11,8,1)="0",2,"")&IF(MID(O11,9,1)="0",1,"")),("("&E1&")")) =IF(F1="",(IF(MID(P11,1,1)="0",9,"")&IF(MID(P11,2,1)="0",8,"")&IF(MID(P11,3,1)="0",7,"")&IF(MID(P11,4,1)="0",6,"")&IF(MID(P11,5,1)="0",5,"")&IF(MID(P11,6,1)="0",4,"")&IF(MID(P11,7,1)="0",3,"")&IF(MID(P11,8,1)="0",2,"")&IF(MID(P11,9,1)="0",1,"")),("("&F1&")")) =IF(G1="",(IF(MID(Q11,1,1)="0",9,"")&IF(MID(Q11,2,1)="0",8,"")&IF(MID(Q11,3,1)="0",7,"")&IF(MID(Q11,4,1)="0",6,"")&IF(MID(Q11,5,1)="0",5,"")&IF(MID(Q11,6,1)="0",4,"")&IF(MID(Q11,7,1)="0",3,"")&IF(MID(Q11,8,1)="0",2,"")&IF(MID(Q11,9,1)="0",1,"")),("("&G1&")")) =IF(H1="",(IF(MID(R11,1,1)="0",9,"")&IF(MID(R11,2,1)="0",8,"")&IF(MID(R11,3,1)="0",7,"")&IF(MID(R11,4,1)="0",6,"")&IF(MID(R11,5,1)="0",5,"")&IF(MID(R11,6,1)="0",4,"")&IF(MID(R11,7,1)="0",3,"")&IF(MID(R11,8,1)="0",2,"")&IF(MID(R11,9,1)="0",1,"")),("("&H1&")")) =IF(I1="",(IF(MID(S11,1,1)="0",9,"")&IF(MID(S11,2,1)="0",8,"")&IF(MID(S11,3,1)="0",7,"")&IF(MID(S11,4,1)="0",6,"")&IF(MID(S11,5,1)="0",5,"")&IF(MID(S11,6,1)="0",4,"")&IF(MID(S11,7,1)="0",3,"")&IF(MID(S11,8,1)="0",2,"")&IF(MID(S11,9,1)="0",1,"")),("("&I1&")")) ="" =MID(K$10+$T1+$V$1+10^9,2,9) =MID(L$10+$T1+$V$1+10^9,2,9) =MID(M$10+$T1+$V$1+10^9,2,9) =MID(N$10+$T1+$W$1+10^9,2,9) =MID(O$10+$T1+$W$1+10^9,2,9) =MID(P$10+$T1+$W$1+10^9,2,9) =MID(Q$10+$T1+$X$1+10^9,2,9) =MID(R$10+$T1+$X$1+10^9,2,9) =MID(S$10+$T1+$X$1+10^9,2,9) ="" ="" ="" ="" ="" =IF(A2="",(IF(MID(K12,1,1)="0",9,"")&IF(MID(K12,2,1)="0",8,"")&IF(MID(K12,3,1)="0",7,"")&IF(MID(K12,4,1)="0",6,"")&IF(MID(K12,5,1)="0",5,"")&IF(MID(K12,6,1)="0",4,"")&IF(MID(K12,7,1)="0",3,"")&IF(MID(K12,8,1)="0",2,"")&IF(MID(K12,9,1)="0",1,"")),("("&A2&")")) =IF(B2="",(IF(MID(L12,1,1)="0",9,"")&IF(MID(L12,2,1)="0",8,"")&IF(MID(L12,3,1)="0",7,"")&IF(MID(L12,4,1)="0",6,"")&IF(MID(L12,5,1)="0",5,"")&IF(MID(L12,6,1)="0",4,"")&IF(MID(L12,7,1)="0",3,"")&IF(MID(L12,8,1)="0",2,"")&IF(MID(L12,9,1)="0",1,"")),("("&B2&")")) =IF(C2="",(IF(MID(M12,1,1)="0",9,"")&IF(MID(M12,2,1)="0",8,"")&IF(MID(M12,3,1)="0",7,"")&IF(MID(M12,4,1)="0",6,"")&IF(MID(M12,5,1)="0",5,"")&IF(MID(M12,6,1)="0",4,"")&IF(MID(M12,7,1)="0",3,"")&IF(MID(M12,8,1)="0",2,"")&IF(MID(M12,9,1)="0",1,"")),("("&C2&")")) =IF(D2="",(IF(MID(N12,1,1)="0",9,"")&IF(MID(N12,2,1)="0",8,"")&IF(MID(N12,3,1)="0",7,"")&IF(MID(N12,4,1)="0",6,"")&IF(MID(N12,5,1)="0",5,"")&IF(MID(N12,6,1)="0",4,"")&IF(MID(N12,7,1)="0",3,"")&IF(MID(N12,8,1)="0",2,"")&IF(MID(N12,9,1)="0",1,"")),("("&D2&")")) =IF(E2="",(IF(MID(O12,1,1)="0",9,"")&IF(MID(O12,2,1)="0",8,"")&IF(MID(O12,3,1)="0",7,"")&IF(MID(O12,4,1)="0",6,"")&IF(MID(O12,5,1)="0",5,"")&IF(MID(O12,6,1)="0",4,"")&IF(MID(O12,7,1)="0",3,"")&IF(MID(O12,8,1)="0",2,"")&IF(MID(O12,9,1)="0",1,"")),("("&E2&")")) =IF(F2="",(IF(MID(P12,1,1)="0",9,"")&IF(MID(P12,2,1)="0",8,"")&IF(MID(P12,3,1)="0",7,"")&IF(MID(P12,4,1)="0",6,"")&IF(MID(P12,5,1)="0",5,"")&IF(MID(P12,6,1)="0",4,"")&IF(MID(P12,7,1)="0",3,"")&IF(MID(P12,8,1)="0",2,"")&IF(MID(P12,9,1)="0",1,"")),("("&F2&")")) =IF(G2="",(IF(MID(Q12,1,1)="0",9,"")&IF(MID(Q12,2,1)="0",8,"")&IF(MID(Q12,3,1)="0",7,"")&IF(MID(Q12,4,1)="0",6,"")&IF(MID(Q12,5,1)="0",5,"")&IF(MID(Q12,6,1)="0",4,"")&IF(MID(Q12,7,1)="0",3,"")&IF(MID(Q12,8,1)="0",2,"")&IF(MID(Q12,9,1)="0",1,"")),("("&G2&")")) =IF(H2="",(IF(MID(R12,1,1)="0",9,"")&IF(MID(R12,2,1)="0",8,"")&IF(MID(R12,3,1)="0",7,"")&IF(MID(R12,4,1)="0",6,"")&IF(MID(R12,5,1)="0",5,"")&IF(MID(R12,6,1)="0",4,"")&IF(MID(R12,7,1)="0",3,"")&IF(MID(R12,8,1)="0",2,"")&IF(MID(R12,9,1)="0",1,"")),("("&H2&")")) =IF(I2="",(IF(MID(S12,1,1)="0",9,"")&IF(MID(S12,2,1)="0",8,"")&IF(MID(S12,3,1)="0",7,"")&IF(MID(S12,4,1)="0",6,"")&IF(MID(S12,5,1)="0",5,"")&IF(MID(S12,6,1)="0",4,"")&IF(MID(S12,7,1)="0",3,"")&IF(MID(S12,8,1)="0",2,"")&IF(MID(S12,9,1)="0",1,"")),("("&I2&")")) ="" =MID(K$10+$T2+$V$1+10^9,2,9) =MID(L$10+$T2+$V$1+10^9,2,9) =MID(M$10+$T2+$V$1+10^9,2,9) =MID(N$10+$T2+$W$1+10^9,2,9) =MID(O$10+$T2+$W$1+10^9,2,9) =MID(P$10+$T2+$W$1+10^9,2,9) =MID(Q$10+$T2+$X$1+10^9,2,9) =MID(R$10+$T2+$X$1+10^9,2,9) =MID(S$10+$T2+$X$1+10^9,2,9) ="" ="" ="" ="" ="" =IF(A3="",(IF(MID(K13,1,1)="0",9,"")&IF(MID(K13,2,1)="0",8,"")&IF(MID(K13,3,1)="0",7,"")&IF(MID(K13,4,1)="0",6,"")&IF(MID(K13,5,1)="0",5,"")&IF(MID(K13,6,1)="0",4,"")&IF(MID(K13,7,1)="0",3,"")&IF(MID(K13,8,1)="0",2,"")&IF(MID(K13,9,1)="0",1,"")),("("&A3&")")) =IF(B3="",(IF(MID(L13,1,1)="0",9,"")&IF(MID(L13,2,1)="0",8,"")&IF(MID(L13,3,1)="0",7,"")&IF(MID(L13,4,1)="0",6,"")&IF(MID(L13,5,1)="0",5,"")&IF(MID(L13,6,1)="0",4,"")&IF(MID(L13,7,1)="0",3,"")&IF(MID(L13,8,1)="0",2,"")&IF(MID(L13,9,1)="0",1,"")),("("&B3&")")) =IF(C3="",(IF(MID(M13,1,1)="0",9,"")&IF(MID(M13,2,1)="0",8,"")&IF(MID(M13,3,1)="0",7,"")&IF(MID(M13,4,1)="0",6,"")&IF(MID(M13,5,1)="0",5,"")&IF(MID(M13,6,1)="0",4,"")&IF(MID(M13,7,1)="0",3,"")&IF(MID(M13,8,1)="0",2,"")&IF(MID(M13,9,1)="0",1,"")),("("&C3&")")) =IF(D3="",(IF(MID(N13,1,1)="0",9,"")&IF(MID(N13,2,1)="0",8,"")&IF(MID(N13,3,1)="0",7,"")&IF(MID(N13,4,1)="0",6,"")&IF(MID(N13,5,1)="0",5,"")&IF(MID(N13,6,1)="0",4,"")&IF(MID(N13,7,1)="0",3,"")&IF(MID(N13,8,1)="0",2,"")&IF(MID(N13,9,1)="0",1,"")),("("&D3&")")) =IF(E3="",(IF(MID(O13,1,1)="0",9,"")&IF(MID(O13,2,1)="0",8,"")&IF(MID(O13,3,1)="0",7,"")&IF(MID(O13,4,1)="0",6,"")&IF(MID(O13,5,1)="0",5,"")&IF(MID(O13,6,1)="0",4,"")&IF(MID(O13,7,1)="0",3,"")&IF(MID(O13,8,1)="0",2,"")&IF(MID(O13,9,1)="0",1,"")),("("&E3&")")) =IF(F3="",(IF(MID(P13,1,1)="0",9,"")&IF(MID(P13,2,1)="0",8,"")&IF(MID(P13,3,1)="0",7,"")&IF(MID(P13,4,1)="0",6,"")&IF(MID(P13,5,1)="0",5,"")&IF(MID(P13,6,1)="0",4,"")&IF(MID(P13,7,1)="0",3,"")&IF(MID(P13,8,1)="0",2,"")&IF(MID(P13,9,1)="0",1,"")),("("&F3&")")) =IF(G3="",(IF(MID(Q13,1,1)="0",9,"")&IF(MID(Q13,2,1)="0",8,"")&IF(MID(Q13,3,1)="0",7,"")&IF(MID(Q13,4,1)="0",6,"")&IF(MID(Q13,5,1)="0",5,"")&IF(MID(Q13,6,1)="0",4,"")&IF(MID(Q13,7,1)="0",3,"")&IF(MID(Q13,8,1)="0",2,"")&IF(MID(Q13,9,1)="0",1,"")),("("&G3&")")) =IF(H3="",(IF(MID(R13,1,1)="0",9,"")&IF(MID(R13,2,1)="0",8,"")&IF(MID(R13,3,1)="0",7,"")&IF(MID(R13,4,1)="0",6,"")&IF(MID(R13,5,1)="0",5,"")&IF(MID(R13,6,1)="0",4,"")&IF(MID(R13,7,1)="0",3,"")&IF(MID(R13,8,1)="0",2,"")&IF(MID(R13,9,1)="0",1,"")),("("&H3&")")) =IF(I3="",(IF(MID(S13,1,1)="0",9,"")&IF(MID(S13,2,1)="0",8,"")&IF(MID(S13,3,1)="0",7,"")&IF(MID(S13,4,1)="0",6,"")&IF(MID(S13,5,1)="0",5,"")&IF(MID(S13,6,1)="0",4,"")&IF(MID(S13,7,1)="0",3,"")&IF(MID(S13,8,1)="0",2,"")&IF(MID(S13,9,1)="0",1,"")),("("&I3&")")) ="" =MID(K$10+$T3+$V$1+10^9,2,9) =MID(L$10+$T3+$V$1+10^9,2,9) =MID(M$10+$T3+$V$1+10^9,2,9) =MID(N$10+$T3+$W$1+10^9,2,9) =MID(O$10+$T3+$W$1+10^9,2,9) =MID(P$10+$T3+$W$1+10^9,2,9) =MID(Q$10+$T3+$X$1+10^9,2,9) =MID(R$10+$T3+$X$1+10^9,2,9) =MID(S$10+$T3+$X$1+10^9,2,9) ="" ="" ="" ="" ="" =IF(A4="",(IF(MID(K14,1,1)="0",9,"")&IF(MID(K14,2,1)="0",8,"")&IF(MID(K14,3,1)="0",7,"")&IF(MID(K14,4,1)="0",6,"")&IF(MID(K14,5,1)="0",5,"")&IF(MID(K14,6,1)="0",4,"")&IF(MID(K14,7,1)="0",3,"")&IF(MID(K14,8,1)="0",2,"")&IF(MID(K14,9,1)="0",1,"")),("("&A4&")")) =IF(B4="",(IF(MID(L14,1,1)="0",9,"")&IF(MID(L14,2,1)="0",8,"")&IF(MID(L14,3,1)="0",7,"")&IF(MID(L14,4,1)="0",6,"")&IF(MID(L14,5,1)="0",5,"")&IF(MID(L14,6,1)="0",4,"")&IF(MID(L14,7,1)="0",3,"")&IF(MID(L14,8,1)="0",2,"")&IF(MID(L14,9,1)="0",1,"")),("("&B4&")")) =IF(C4="",(IF(MID(M14,1,1)="0",9,"")&IF(MID(M14,2,1)="0",8,"")&IF(MID(M14,3,1)="0",7,"")&IF(MID(M14,4,1)="0",6,"")&IF(MID(M14,5,1)="0",5,"")&IF(MID(M14,6,1)="0",4,"")&IF(MID(M14,7,1)="0",3,"")&IF(MID(M14,8,1)="0",2,"")&IF(MID(M14,9,1)="0",1,"")),("("&C4&")")) =IF(D4="",(IF(MID(N14,1,1)="0",9,"")&IF(MID(N14,2,1)="0",8,"")&IF(MID(N14,3,1)="0",7,"")&IF(MID(N14,4,1)="0",6,"")&IF(MID(N14,5,1)="0",5,"")&IF(MID(N14,6,1)="0",4,"")&IF(MID(N14,7,1)="0",3,"")&IF(MID(N14,8,1)="0",2,"")&IF(MID(N14,9,1)="0",1,"")),("("&D4&")")) =IF(E4="",(IF(MID(O14,1,1)="0",9,"")&IF(MID(O14,2,1)="0",8,"")&IF(MID(O14,3,1)="0",7,"")&IF(MID(O14,4,1)="0",6,"")&IF(MID(O14,5,1)="0",5,"")&IF(MID(O14,6,1)="0",4,"")&IF(MID(O14,7,1)="0",3,"")&IF(MID(O14,8,1)="0",2,"")&IF(MID(O14,9,1)="0",1,"")),("("&E4&")")) =IF(F4="",(IF(MID(P14,1,1)="0",9,"")&IF(MID(P14,2,1)="0",8,"")&IF(MID(P14,3,1)="0",7,"")&IF(MID(P14,4,1)="0",6,"")&IF(MID(P14,5,1)="0",5,"")&IF(MID(P14,6,1)="0",4,"")&IF(MID(P14,7,1)="0",3,"")&IF(MID(P14,8,1)="0",2,"")&IF(MID(P14,9,1)="0",1,"")),("("&F4&")")) =IF(G4="",(IF(MID(Q14,1,1)="0",9,"")&IF(MID(Q14,2,1)="0",8,"")&IF(MID(Q14,3,1)="0",7,"")&IF(MID(Q14,4,1)="0",6,"")&IF(MID(Q14,5,1)="0",5,"")&IF(MID(Q14,6,1)="0",4,"")&IF(MID(Q14,7,1)="0",3,"")&IF(MID(Q14,8,1)="0",2,"")&IF(MID(Q14,9,1)="0",1,"")),("("&G4&")")) =IF(H4="",(IF(MID(R14,1,1)="0",9,"")&IF(MID(R14,2,1)="0",8,"")&IF(MID(R14,3,1)="0",7,"")&IF(MID(R14,4,1)="0",6,"")&IF(MID(R14,5,1)="0",5,"")&IF(MID(R14,6,1)="0",4,"")&IF(MID(R14,7,1)="0",3,"")&IF(MID(R14,8,1)="0",2,"")&IF(MID(R14,9,1)="0",1,"")),("("&H4&")")) =IF(I4="",(IF(MID(S14,1,1)="0",9,"")&IF(MID(S14,2,1)="0",8,"")&IF(MID(S14,3,1)="0",7,"")&IF(MID(S14,4,1)="0",6,"")&IF(MID(S14,5,1)="0",5,"")&IF(MID(S14,6,1)="0",4,"")&IF(MID(S14,7,1)="0",3,"")&IF(MID(S14,8,1)="0",2,"")&IF(MID(S14,9,1)="0",1,"")),("("&I4&")")) ="" =MID(K$10+$T4+$V$4+10^9,2,9) =MID(L$10+$T4+$V$4+10^9,2,9) =MID(M$10+$T4+$V$4+10^9,2,9) =MID(N$10+$T4+$W$4+10^9,2,9) =MID(O$10+$T4+$W$4+10^9,2,9) =MID(P$10+$T4+$W$4+10^9,2,9) =MID(Q$10+$T4+$X$4+10^9,2,9) =MID(R$10+$T4+$X$4+10^9,2,9) =MID(S$10+$T4+$X$4+10^9,2,9) ="" ="" ="" ="" ="" =IF(A5="",(IF(MID(K15,1,1)="0",9,"")&IF(MID(K15,2,1)="0",8,"")&IF(MID(K15,3,1)="0",7,"")&IF(MID(K15,4,1)="0",6,"")&IF(MID(K15,5,1)="0",5,"")&IF(MID(K15,6,1)="0",4,"")&IF(MID(K15,7,1)="0",3,"")&IF(MID(K15,8,1)="0",2,"")&IF(MID(K15,9,1)="0",1,"")),("("&A5&")")) =IF(B5="",(IF(MID(L15,1,1)="0",9,"")&IF(MID(L15,2,1)="0",8,"")&IF(MID(L15,3,1)="0",7,"")&IF(MID(L15,4,1)="0",6,"")&IF(MID(L15,5,1)="0",5,"")&IF(MID(L15,6,1)="0",4,"")&IF(MID(L15,7,1)="0",3,"")&IF(MID(L15,8,1)="0",2,"")&IF(MID(L15,9,1)="0",1,"")),("("&B5&")")) =IF(C5="",(IF(MID(M15,1,1)="0",9,"")&IF(MID(M15,2,1)="0",8,"")&IF(MID(M15,3,1)="0",7,"")&IF(MID(M15,4,1)="0",6,"")&IF(MID(M15,5,1)="0",5,"")&IF(MID(M15,6,1)="0",4,"")&IF(MID(M15,7,1)="0",3,"")&IF(MID(M15,8,1)="0",2,"")&IF(MID(M15,9,1)="0",1,"")),("("&C5&")")) =IF(D5="",(IF(MID(N15,1,1)="0",9,"")&IF(MID(N15,2,1)="0",8,"")&IF(MID(N15,3,1)="0",7,"")&IF(MID(N15,4,1)="0",6,"")&IF(MID(N15,5,1)="0",5,"")&IF(MID(N15,6,1)="0",4,"")&IF(MID(N15,7,1)="0",3,"")&IF(MID(N15,8,1)="0",2,"")&IF(MID(N15,9,1)="0",1,"")),("("&D5&")")) =IF(E5="",(IF(MID(O15,1,1)="0",9,"")&IF(MID(O15,2,1)="0",8,"")&IF(MID(O15,3,1)="0",7,"")&IF(MID(O15,4,1)="0",6,"")&IF(MID(O15,5,1)="0",5,"")&IF(MID(O15,6,1)="0",4,"")&IF(MID(O15,7,1)="0",3,"")&IF(MID(O15,8,1)="0",2,"")&IF(MID(O15,9,1)="0",1,"")),("("&E5&")")) =IF(F5="",(IF(MID(P15,1,1)="0",9,"")&IF(MID(P15,2,1)="0",8,"")&IF(MID(P15,3,1)="0",7,"")&IF(MID(P15,4,1)="0",6,"")&IF(MID(P15,5,1)="0",5,"")&IF(MID(P15,6,1)="0",4,"")&IF(MID(P15,7,1)="0",3,"")&IF(MID(P15,8,1)="0",2,"")&IF(MID(P15,9,1)="0",1,"")),("("&F5&")")) =IF(G5="",(IF(MID(Q15,1,1)="0",9,"")&IF(MID(Q15,2,1)="0",8,"")&IF(MID(Q15,3,1)="0",7,"")&IF(MID(Q15,4,1)="0",6,"")&IF(MID(Q15,5,1)="0",5,"")&IF(MID(Q15,6,1)="0",4,"")&IF(MID(Q15,7,1)="0",3,"")&IF(MID(Q15,8,1)="0",2,"")&IF(MID(Q15,9,1)="0",1,"")),("("&G5&")")) =IF(H5="",(IF(MID(R15,1,1)="0",9,"")&IF(MID(R15,2,1)="0",8,"")&IF(MID(R15,3,1)="0",7,"")&IF(MID(R15,4,1)="0",6,"")&IF(MID(R15,5,1)="0",5,"")&IF(MID(R15,6,1)="0",4,"")&IF(MID(R15,7,1)="0",3,"")&IF(MID(R15,8,1)="0",2,"")&IF(MID(R15,9,1)="0",1,"")),("("&H5&")")) =IF(I5="",(IF(MID(S15,1,1)="0",9,"")&IF(MID(S15,2,1)="0",8,"")&IF(MID(S15,3,1)="0",7,"")&IF(MID(S15,4,1)="0",6,"")&IF(MID(S15,5,1)="0",5,"")&IF(MID(S15,6,1)="0",4,"")&IF(MID(S15,7,1)="0",3,"")&IF(MID(S15,8,1)="0",2,"")&IF(MID(S15,9,1)="0",1,"")),("("&I5&")")) ="" =MID(K$10+$T5+$V$4+10^9,2,9) =MID(L$10+$T5+$V$4+10^9,2,9) =MID(M$10+$T5+$V$4+10^9,2,9) =MID(N$10+$T5+$W$4+10^9,2,9) =MID(O$10+$T5+$W$4+10^9,2,9) =MID(P$10+$T5+$W$4+10^9,2,9) =MID(Q$10+$T5+$X$4+10^9,2,9) =MID(R$10+$T5+$X$4+10^9,2,9) =MID(S$10+$T5+$X$4+10^9,2,9) ="" ="" ="" ="" ="" =IF(A6="",(IF(MID(K16,1,1)="0",9,"")&IF(MID(K16,2,1)="0",8,"")&IF(MID(K16,3,1)="0",7,"")&IF(MID(K16,4,1)="0",6,"")&IF(MID(K16,5,1)="0",5,"")&IF(MID(K16,6,1)="0",4,"")&IF(MID(K16,7,1)="0",3,"")&IF(MID(K16,8,1)="0",2,"")&IF(MID(K16,9,1)="0",1,"")),("("&A6&")")) =IF(B6="",(IF(MID(L16,1,1)="0",9,"")&IF(MID(L16,2,1)="0",8,"")&IF(MID(L16,3,1)="0",7,"")&IF(MID(L16,4,1)="0",6,"")&IF(MID(L16,5,1)="0",5,"")&IF(MID(L16,6,1)="0",4,"")&IF(MID(L16,7,1)="0",3,"")&IF(MID(L16,8,1)="0",2,"")&IF(MID(L16,9,1)="0",1,"")),("("&B6&")")) =IF(C6="",(IF(MID(M16,1,1)="0",9,"")&IF(MID(M16,2,1)="0",8,"")&IF(MID(M16,3,1)="0",7,"")&IF(MID(M16,4,1)="0",6,"")&IF(MID(M16,5,1)="0",5,"")&IF(MID(M16,6,1)="0",4,"")&IF(MID(M16,7,1)="0",3,"")&IF(MID(M16,8,1)="0",2,"")&IF(MID(M16,9,1)="0",1,"")),("("&C6&")")) =IF(D6="",(IF(MID(N16,1,1)="0",9,"")&IF(MID(N16,2,1)="0",8,"")&IF(MID(N16,3,1)="0",7,"")&IF(MID(N16,4,1)="0",6,"")&IF(MID(N16,5,1)="0",5,"")&IF(MID(N16,6,1)="0",4,"")&IF(MID(N16,7,1)="0",3,"")&IF(MID(N16,8,1)="0",2,"")&IF(MID(N16,9,1)="0",1,"")),("("&D6&")")) =IF(E6="",(IF(MID(O16,1,1)="0",9,"")&IF(MID(O16,2,1)="0",8,"")&IF(MID(O16,3,1)="0",7,"")&IF(MID(O16,4,1)="0",6,"")&IF(MID(O16,5,1)="0",5,"")&IF(MID(O16,6,1)="0",4,"")&IF(MID(O16,7,1)="0",3,"")&IF(MID(O16,8,1)="0",2,"")&IF(MID(O16,9,1)="0",1,"")),("("&E6&")")) =IF(F6="",(IF(MID(P16,1,1)="0",9,"")&IF(MID(P16,2,1)="0",8,"")&IF(MID(P16,3,1)="0",7,"")&IF(MID(P16,4,1)="0",6,"")&IF(MID(P16,5,1)="0",5,"")&IF(MID(P16,6,1)="0",4,"")&IF(MID(P16,7,1)="0",3,"")&IF(MID(P16,8,1)="0",2,"")&IF(MID(P16,9,1)="0",1,"")),("("&F6&")")) =IF(G6="",(IF(MID(Q16,1,1)="0",9,"")&IF(MID(Q16,2,1)="0",8,"")&IF(MID(Q16,3,1)="0",7,"")&IF(MID(Q16,4,1)="0",6,"")&IF(MID(Q16,5,1)="0",5,"")&IF(MID(Q16,6,1)="0",4,"")&IF(MID(Q16,7,1)="0",3,"")&IF(MID(Q16,8,1)="0",2,"")&IF(MID(Q16,9,1)="0",1,"")),("("&G6&")")) =IF(H6="",(IF(MID(R16,1,1)="0",9,"")&IF(MID(R16,2,1)="0",8,"")&IF(MID(R16,3,1)="0",7,"")&IF(MID(R16,4,1)="0",6,"")&IF(MID(R16,5,1)="0",5,"")&IF(MID(R16,6,1)="0",4,"")&IF(MID(R16,7,1)="0",3,"")&IF(MID(R16,8,1)="0",2,"")&IF(MID(R16,9,1)="0",1,"")),("("&H6&")")) =IF(I6="",(IF(MID(S16,1,1)="0",9,"")&IF(MID(S16,2,1)="0",8,"")&IF(MID(S16,3,1)="0",7,"")&IF(MID(S16,4,1)="0",6,"")&IF(MID(S16,5,1)="0",5,"")&IF(MID(S16,6,1)="0",4,"")&IF(MID(S16,7,1)="0",3,"")&IF(MID(S16,8,1)="0",2,"")&IF(MID(S16,9,1)="0",1,"")),("("&I6&")")) ="" =MID(K$10+$T6+$V$4+10^9,2,9) =MID(L$10+$T6+$V$4+10^9,2,9) =MID(M$10+$T6+$V$4+10^9,2,9) =MID(N$10+$T6+$W$4+10^9,2,9) =MID(O$10+$T6+$W$4+10^9,2,9) =MID(P$10+$T6+$W$4+10^9,2,9) =MID(Q$10+$T6+$X$4+10^9,2,9) =MID(R$10+$T6+$X$4+10^9,2,9) =MID(S$10+$T6+$X$4+10^9,2,9) ="" ="" ="" ="" ="" =IF(A7="",(IF(MID(K17,1,1)="0",9,"")&IF(MID(K17,2,1)="0",8,"")&IF(MID(K17,3,1)="0",7,"")&IF(MID(K17,4,1)="0",6,"")&IF(MID(K17,5,1)="0",5,"")&IF(MID(K17,6,1)="0",4,"")&IF(MID(K17,7,1)="0",3,"")&IF(MID(K17,8,1)="0",2,"")&IF(MID(K17,9,1)="0",1,"")),("("&A7&")")) =IF(B7="",(IF(MID(L17,1,1)="0",9,"")&IF(MID(L17,2,1)="0",8,"")&IF(MID(L17,3,1)="0",7,"")&IF(MID(L17,4,1)="0",6,"")&IF(MID(L17,5,1)="0",5,"")&IF(MID(L17,6,1)="0",4,"")&IF(MID(L17,7,1)="0",3,"")&IF(MID(L17,8,1)="0",2,"")&IF(MID(L17,9,1)="0",1,"")),("("&B7&")")) =IF(C7="",(IF(MID(M17,1,1)="0",9,"")&IF(MID(M17,2,1)="0",8,"")&IF(MID(M17,3,1)="0",7,"")&IF(MID(M17,4,1)="0",6,"")&IF(MID(M17,5,1)="0",5,"")&IF(MID(M17,6,1)="0",4,"")&IF(MID(M17,7,1)="0",3,"")&IF(MID(M17,8,1)="0",2,"")&IF(MID(M17,9,1)="0",1,"")),("("&C7&")")) =IF(D7="",(IF(MID(N17,1,1)="0",9,"")&IF(MID(N17,2,1)="0",8,"")&IF(MID(N17,3,1)="0",7,"")&IF(MID(N17,4,1)="0",6,"")&IF(MID(N17,5,1)="0",5,"")&IF(MID(N17,6,1)="0",4,"")&IF(MID(N17,7,1)="0",3,"")&IF(MID(N17,8,1)="0",2,"")&IF(MID(N17,9,1)="0",1,"")),("("&D7&")")) =IF(E7="",(IF(MID(O17,1,1)="0",9,"")&IF(MID(O17,2,1)="0",8,"")&IF(MID(O17,3,1)="0",7,"")&IF(MID(O17,4,1)="0",6,"")&IF(MID(O17,5,1)="0",5,"")&IF(MID(O17,6,1)="0",4,"")&IF(MID(O17,7,1)="0",3,"")&IF(MID(O17,8,1)="0",2,"")&IF(MID(O17,9,1)="0",1,"")),("("&E7&")")) =IF(F7="",(IF(MID(P17,1,1)="0",9,"")&IF(MID(P17,2,1)="0",8,"")&IF(MID(P17,3,1)="0",7,"")&IF(MID(P17,4,1)="0",6,"")&IF(MID(P17,5,1)="0",5,"")&IF(MID(P17,6,1)="0",4,"")&IF(MID(P17,7,1)="0",3,"")&IF(MID(P17,8,1)="0",2,"")&IF(MID(P17,9,1)="0",1,"")),("("&F7&")")) =IF(G7="",(IF(MID(Q17,1,1)="0",9,"")&IF(MID(Q17,2,1)="0",8,"")&IF(MID(Q17,3,1)="0",7,"")&IF(MID(Q17,4,1)="0",6,"")&IF(MID(Q17,5,1)="0",5,"")&IF(MID(Q17,6,1)="0",4,"")&IF(MID(Q17,7,1)="0",3,"")&IF(MID(Q17,8,1)="0",2,"")&IF(MID(Q17,9,1)="0",1,"")),("("&G7&")")) =IF(H7="",(IF(MID(R17,1,1)="0",9,"")&IF(MID(R17,2,1)="0",8,"")&IF(MID(R17,3,1)="0",7,"")&IF(MID(R17,4,1)="0",6,"")&IF(MID(R17,5,1)="0",5,"")&IF(MID(R17,6,1)="0",4,"")&IF(MID(R17,7,1)="0",3,"")&IF(MID(R17,8,1)="0",2,"")&IF(MID(R17,9,1)="0",1,"")),("("&H7&")")) =IF(I7="",(IF(MID(S17,1,1)="0",9,"")&IF(MID(S17,2,1)="0",8,"")&IF(MID(S17,3,1)="0",7,"")&IF(MID(S17,4,1)="0",6,"")&IF(MID(S17,5,1)="0",5,"")&IF(MID(S17,6,1)="0",4,"")&IF(MID(S17,7,1)="0",3,"")&IF(MID(S17,8,1)="0",2,"")&IF(MID(S17,9,1)="0",1,"")),("("&I7&")")) ="" =MID(K$10+$T7+$V$7+10^9,2,9) =MID(L$10+$T7+$V$7+10^9,2,9) =MID(M$10+$T7+$V$7+10^9,2,9) =MID(N$10+$T7+$W$7+10^9,2,9) =MID(O$10+$T7+$W$7+10^9,2,9) =MID(P$10+$T7+$W$7+10^9,2,9) =MID(Q$10+$T7+$X$7+10^9,2,9) =MID(R$10+$T7+$X$7+10^9,2,9) =MID(S$10+$T7+$X$7+10^9,2,9) ="" ="" ="" ="" ="" =IF(A8="",(IF(MID(K18,1,1)="0",9,"")&IF(MID(K18,2,1)="0",8,"")&IF(MID(K18,3,1)="0",7,"")&IF(MID(K18,4,1)="0",6,"")&IF(MID(K18,5,1)="0",5,"")&IF(MID(K18,6,1)="0",4,"")&IF(MID(K18,7,1)="0",3,"")&IF(MID(K18,8,1)="0",2,"")&IF(MID(K18,9,1)="0",1,"")),("("&A8&")")) =IF(B8="",(IF(MID(L18,1,1)="0",9,"")&IF(MID(L18,2,1)="0",8,"")&IF(MID(L18,3,1)="0",7,"")&IF(MID(L18,4,1)="0",6,"")&IF(MID(L18,5,1)="0",5,"")&IF(MID(L18,6,1)="0",4,"")&IF(MID(L18,7,1)="0",3,"")&IF(MID(L18,8,1)="0",2,"")&IF(MID(L18,9,1)="0",1,"")),("("&B8&")")) =IF(C8="",(IF(MID(M18,1,1)="0",9,"")&IF(MID(M18,2,1)="0",8,"")&IF(MID(M18,3,1)="0",7,"")&IF(MID(M18,4,1)="0",6,"")&IF(MID(M18,5,1)="0",5,"")&IF(MID(M18,6,1)="0",4,"")&IF(MID(M18,7,1)="0",3,"")&IF(MID(M18,8,1)="0",2,"")&IF(MID(M18,9,1)="0",1,"")),("("&C8&")")) =IF(D8="",(IF(MID(N18,1,1)="0",9,"")&IF(MID(N18,2,1)="0",8,"")&IF(MID(N18,3,1)="0",7,"")&IF(MID(N18,4,1)="0",6,"")&IF(MID(N18,5,1)="0",5,"")&IF(MID(N18,6,1)="0",4,"")&IF(MID(N18,7,1)="0",3,"")&IF(MID(N18,8,1)="0",2,"")&IF(MID(N18,9,1)="0",1,"")),("("&D8&")")) =IF(E8="",(IF(MID(O18,1,1)="0",9,"")&IF(MID(O18,2,1)="0",8,"")&IF(MID(O18,3,1)="0",7,"")&IF(MID(O18,4,1)="0",6,"")&IF(MID(O18,5,1)="0",5,"")&IF(MID(O18,6,1)="0",4,"")&IF(MID(O18,7,1)="0",3,"")&IF(MID(O18,8,1)="0",2,"")&IF(MID(O18,9,1)="0",1,"")),("("&E8&")")) =IF(F8="",(IF(MID(P18,1,1)="0",9,"")&IF(MID(P18,2,1)="0",8,"")&IF(MID(P18,3,1)="0",7,"")&IF(MID(P18,4,1)="0",6,"")&IF(MID(P18,5,1)="0",5,"")&IF(MID(P18,6,1)="0",4,"")&IF(MID(P18,7,1)="0",3,"")&IF(MID(P18,8,1)="0",2,"")&IF(MID(P18,9,1)="0",1,"")),("("&F8&")")) =IF(G8="",(IF(MID(Q18,1,1)="0",9,"")&IF(MID(Q18,2,1)="0",8,"")&IF(MID(Q18,3,1)="0",7,"")&IF(MID(Q18,4,1)="0",6,"")&IF(MID(Q18,5,1)="0",5,"")&IF(MID(Q18,6,1)="0",4,"")&IF(MID(Q18,7,1)="0",3,"")&IF(MID(Q18,8,1)="0",2,"")&IF(MID(Q18,9,1)="0",1,"")),("("&G8&")")) =IF(H8="",(IF(MID(R18,1,1)="0",9,"")&IF(MID(R18,2,1)="0",8,"")&IF(MID(R18,3,1)="0",7,"")&IF(MID(R18,4,1)="0",6,"")&IF(MID(R18,5,1)="0",5,"")&IF(MID(R18,6,1)="0",4,"")&IF(MID(R18,7,1)="0",3,"")&IF(MID(R18,8,1)="0",2,"")&IF(MID(R18,9,1)="0",1,"")),("("&H8&")")) =IF(I8="",(IF(MID(S18,1,1)="0",9,"")&IF(MID(S18,2,1)="0",8,"")&IF(MID(S18,3,1)="0",7,"")&IF(MID(S18,4,1)="0",6,"")&IF(MID(S18,5,1)="0",5,"")&IF(MID(S18,6,1)="0",4,"")&IF(MID(S18,7,1)="0",3,"")&IF(MID(S18,8,1)="0",2,"")&IF(MID(S18,9,1)="0",1,"")),("("&I8&")")) ="" =MID(K$10+$T8+$V$7+10^9,2,9) =MID(L$10+$T8+$V$7+10^9,2,9) =MID(M$10+$T8+$V$7+10^9,2,9) =MID(N$10+$T8+$W$7+10^9,2,9) =MID(O$10+$T8+$W$7+10^9,2,9) =MID(P$10+$T8+$W$7+10^9,2,9) =MID(Q$10+$T8+$X$7+10^9,2,9) =MID(R$10+$T8+$X$7+10^9,2,9) =MID(S$10+$T8+$X$7+10^9,2,9) ="" ="" ="" ="" ="" =IF(A9="",(IF(MID(K19,1,1)="0",9,"")&IF(MID(K19,2,1)="0",8,"")&IF(MID(K19,3,1)="0",7,"")&IF(MID(K19,4,1)="0",6,"")&IF(MID(K19,5,1)="0",5,"")&IF(MID(K19,6,1)="0",4,"")&IF(MID(K19,7,1)="0",3,"")&IF(MID(K19,8,1)="0",2,"")&IF(MID(K19,9,1)="0",1,"")),("("&A9&")")) =IF(B9="",(IF(MID(L19,1,1)="0",9,"")&IF(MID(L19,2,1)="0",8,"")&IF(MID(L19,3,1)="0",7,"")&IF(MID(L19,4,1)="0",6,"")&IF(MID(L19,5,1)="0",5,"")&IF(MID(L19,6,1)="0",4,"")&IF(MID(L19,7,1)="0",3,"")&IF(MID(L19,8,1)="0",2,"")&IF(MID(L19,9,1)="0",1,"")),("("&B9&")")) =IF(C9="",(IF(MID(M19,1,1)="0",9,"")&IF(MID(M19,2,1)="0",8,"")&IF(MID(M19,3,1)="0",7,"")&IF(MID(M19,4,1)="0",6,"")&IF(MID(M19,5,1)="0",5,"")&IF(MID(M19,6,1)="0",4,"")&IF(MID(M19,7,1)="0",3,"")&IF(MID(M19,8,1)="0",2,"")&IF(MID(M19,9,1)="0",1,"")),("("&C9&")")) =IF(D9="",(IF(MID(N19,1,1)="0",9,"")&IF(MID(N19,2,1)="0",8,"")&IF(MID(N19,3,1)="0",7,"")&IF(MID(N19,4,1)="0",6,"")&IF(MID(N19,5,1)="0",5,"")&IF(MID(N19,6,1)="0",4,"")&IF(MID(N19,7,1)="0",3,"")&IF(MID(N19,8,1)="0",2,"")&IF(MID(N19,9,1)="0",1,"")),("("&D9&")")) =IF(E9="",(IF(MID(O19,1,1)="0",9,"")&IF(MID(O19,2,1)="0",8,"")&IF(MID(O19,3,1)="0",7,"")&IF(MID(O19,4,1)="0",6,"")&IF(MID(O19,5,1)="0",5,"")&IF(MID(O19,6,1)="0",4,"")&IF(MID(O19,7,1)="0",3,"")&IF(MID(O19,8,1)="0",2,"")&IF(MID(O19,9,1)="0",1,"")),("("&E9&")")) =IF(F9="",(IF(MID(P19,1,1)="0",9,"")&IF(MID(P19,2,1)="0",8,"")&IF(MID(P19,3,1)="0",7,"")&IF(MID(P19,4,1)="0",6,"")&IF(MID(P19,5,1)="0",5,"")&IF(MID(P19,6,1)="0",4,"")&IF(MID(P19,7,1)="0",3,"")&IF(MID(P19,8,1)="0",2,"")&IF(MID(P19,9,1)="0",1,"")),("("&F9&")")) =IF(G9="",(IF(MID(Q19,1,1)="0",9,"")&IF(MID(Q19,2,1)="0",8,"")&IF(MID(Q19,3,1)="0",7,"")&IF(MID(Q19,4,1)="0",6,"")&IF(MID(Q19,5,1)="0",5,"")&IF(MID(Q19,6,1)="0",4,"")&IF(MID(Q19,7,1)="0",3,"")&IF(MID(Q19,8,1)="0",2,"")&IF(MID(Q19,9,1)="0",1,"")),("("&G9&")")) =IF(H9="",(IF(MID(R19,1,1)="0",9,"")&IF(MID(R19,2,1)="0",8,"")&IF(MID(R19,3,1)="0",7,"")&IF(MID(R19,4,1)="0",6,"")&IF(MID(R19,5,1)="0",5,"")&IF(MID(R19,6,1)="0",4,"")&IF(MID(R19,7,1)="0",3,"")&IF(MID(R19,8,1)="0",2,"")&IF(MID(R19,9,1)="0",1,"")),("("&H9&")")) =IF(I9="",(IF(MID(S19,1,1)="0",9,"")&IF(MID(S19,2,1)="0",8,"")&IF(MID(S19,3,1)="0",7,"")&IF(MID(S19,4,1)="0",6,"")&IF(MID(S19,5,1)="0",5,"")&IF(MID(S19,6,1)="0",4,"")&IF(MID(S19,7,1)="0",3,"")&IF(MID(S19,8,1)="0",2,"")&IF(MID(S19,9,1)="0",1,"")),("("&I9&")")) ="" =MID(K$10+$T9+$V$7+10^9,2,9) =MID(L$10+$T9+$V$7+10^9,2,9) =MID(M$10+$T9+$V$7+10^9,2,9) =MID(N$10+$T9+$W$7+10^9,2,9) =MID(O$10+$T9+$W$7+10^9,2,9) =MID(P$10+$T9+$W$7+10^9,2,9) =MID(Q$10+$T9+$X$7+10^9,2,9) =MID(R$10+$T9+$X$7+10^9,2,9) =MID(S$10+$T9+$X$7+10^9,2,9) ="" ="" ="" ="" =""
2022年2月1日
もう少しで ２０２１年が終わろうとしています。
でも まだ有言が実行できていません。
今年中にお伝えしますと言っていたのにです。
今現在 文章と画像での表現に苦慮しっぱなしで
今年中には 無理と判断し
今 筆をとっています。どうもすみませんでした。
年が変わってからは 今までとは違った表現で
動画もふくめて 発表してゆこうと心に決めています。
良いお年を
2021年12月31日
現在 有言を実行しようとしているところですが 急いでお伝えしたいことが
前回 諸量の数式表現 のエクセルデータを載せました。
Excel などに転記できるように 範囲を色付けしたものですが
後日 正しく機能するかブログのデータから 転記し確認したところ
うまくゆかないこともあることが分かりました。
データ最初の文字が " 名称" と 半角スペースが入っていたからでした。
半角を含んでコピーしないと 意図した動作ができなかったのです。
変更をしておきました。
私のデータを取り込んでみようとしてくださったかたの中には
こけおどし として 作業停止されたかもしれません。
表形式の 文字列は html を Excel で 手作業で作成しています。
今回作成した表が 今まで゛の中で 一番大きなものでした。
*追伸
上記の 方法でも うまくゆかないこともありました。
回避する 別の方法は
一旦 メモ帳などに転記し それをコピーして から
Excel に落してください。
2021年12月20日
久しぶりの投稿です。
近々に ダイヤモンド結晶模型の製作について載せる段取りをしています。
四角棒を素材にしたのと 丸棒での模型です。今年中にやります。
実際に 目の前で作業をし少し説明すれば分かるようなことが
文章や 画像だけで表現するのは 私には大変困難な作業です。
顔も声も出さずにできるなら YouTube に載せようかなとも 検討しています。
今回 お伝えしようとしているのは 諸量の数式表現のデータです。
今まで お伝えしていた諸量の数値をほとんど網羅しています。
Excelやその同等品に転記してください。
画面には出ていませんが かなりボリュームがあるものです。
* 後日 数式の転記作業で 不本意な事象が発生する場合もあることが判明しました。
その回避方法を 次の回のエピソードでお伝えしています。
名称 面積 体積 基本数 頂芯寸 稜芯寸 S面芯寸 M面芯寸 L面芯寸 仰角 S接合角 M接合角 L接合角 S面角 M面角 L面角 二面角1 二面角2 二面角3
01[3,3,3] =SQRT(3) =1/(6*SQRT(2)) =1/SQRT(3) =SQRT(3/2)/2 =1/4*SQRT(2) =1/12*SQRT(6) =180/PI()*(ASIN(SQRT(2/3))) =60 =180/PI()*(ASIN(1/SQRT(3))) =180/PI()*(2*ASIN(1/SQRT(3))) SS
02[3,3,3,3] =2*SQRT(3) =SQRT(2)/3 =1/SQRT(2) =SQRT(2)/2 =1/2 =1/SQRT(6) =45 =45 =180/PI()*(ACOS(1/SQRT(3))) =180/PI()*(ACOS(1/SQRT(3))*2) SS
03[4,4,4] =6 =1 =SQRT(2/3) =SQRT(3)/2 =SQRT((1/2*SQRT(3))^2-(1/2)^2) =1/2 =180/PI()*(ASIN(1/SQRT(3))) =60 =45 =90 SS
04[3,3,3,3,3] =5*SQRT(3) =5/12*(3+SQRT(5)) =SQRT(1/10*(5+SQRT(5))) =1/4*SQRT(10 + 2*SQRT(5)) =1/4*(1+SQRT(5)) =1/12*(SQRT(15) + 3*SQRT(3)) =180/PI()*(ASIN(2/SQRT(10 + 2*SQRT(5)))) =36 =180/PI()*(ASIN((1 + SQRT(5))/(2*SQRT(3)))) =180/PI()*(ASIN((1 + SQRT(5))/(2*SQRT(3)))*2) SS
05[3,4,3,4] =2*(3+SQRT(3)) =5*SQRT(2)/3 =SQRT(3)/2 =1 =SQRT(3)/2 =1/3*SQRT(6) =1/SQRT(2) =30 =180/PI()*(ASIN(1/SQRT(3))) =180/PI()*(ASIN(SQRT(2/3))) =180/PI()*(ACOS(1/3)) =180/PI()*(ACOS(1/SQRT(3))) =180/PI()*(ACOS(1/SQRT(3))+ACOS(1/3)) SM
06[3,6,6] =7*SQRT(3) =23/(6*SQRT(2)) =3/SQRT(11) =SQRT(22)/4 =1/4*(3*SQRT(2)) =1/12*(5*SQRT(6)) =1/4*SQRT(6) =180/PI()*(ASIN(SQRT(2/11))) =180/PI()*(ASIN(SQRT(11)/6)) =180/PI()*(ASIN(SQRT(11/3)/2)) =180/PI()*(ACOS(SQRT(2/3)/3)) =180/PI()*(ACOS(SQRT(2/3))) =180/PI()*(ACOS(SQRT(2/3)/3)+ACOS(SQRT(2/3))) =180/PI()*(2*ACOS(SQRT(2/3))) SM MM
07[3,3,3,3,4] =6+8*SQRT(3) =1/3*SQRT(188 + (3*(2149479 - 15037*SQRT(33)))^(1/3) + (3*(2149479 + 15037*SQRT(33)))^(1/3)) =1/SQRT(42/(20 + (566 - 42*SQRT(33))^(1/3) + (566 + 42*SQRT(33))^(1/3))) =SQRT(-(21/(2*(-22+(566-42*SQRT(33))^(1/3)+(566+42*SQRT(33))^(1/3))))) =1/(2*SQRT(3/(7 + (199 - 3*SQRT(33))^(1/3) + (199 + 3*SQRT(33))^(1/3)))) =1/(2*SQRT(3/(6 + (199 - 3*SQRT(33))^(1/3) + (199 + 3*SQRT(33))^(1/3)))) =1/(2*SQRT(3/(4 + (199 - 3*SQRT(33))^(1/3) + (199 + 3*SQRT(33))^(1/3)))) =180/PI()*(ASIN(1/SQRT(42/(22 - (566 - 42*SQRT(33))^(1/3) - (566 + 42*SQRT(33))^(1/3))))) =180/PI()*(ASIN(SQRT(21/(2*(20 + (566 - 42*SQRT(33))^(1/3) + (566 + 42*SQRT(33))^(1/3)))))) =180/PI()*(ASIN(SQRT(21/(20 + (566 - 42*SQRT(33))^(1/3) + (566 + 42*SQRT(33))^(1/3))))) =180/PI()*(ACOS(1/SQRT(7 + (199 - 3*SQRT(33))^(1/3) + (199 + 3*SQRT(33))^(1/3)))) =180/PI()*(ACOS(SQRT(3/(7 + (199 - 3*SQRT(33))^(1/3) + (199 + 3*SQRT(33))^(1/3))))) =180/PI()*(2*(ACOS(1/SQRT(7 + (199 - 3*SQRT(33))^(1/3) + (199 + 3*SQRT(33))^(1/3))))) =180/PI()*(ACOS(1/SQRT(7 + (199 - 3*SQRT(33))^(1/3) + (199 + 3*SQRT(33))^(1/3)))+ACOS(SQRT(3/(7 + (199 - 3*SQRT(33))^(1/3) + (199 + 3*SQRT(33))^(1/3))))) SS SM
08[3,4,4,4] =2*(9+SQRT(3)) =4+10*SQRT(2)/3 =1/17*SQRT(34*(6 + SQRT(2))) =1/2*SQRT(5+2*SQRT(2)) =1/2*SQRT(4 + 2*SQRT(2)) =SQRT(3)/2 + 1/SQRT(6) =1/2 + 1/SQRT(2) =180/PI()*(ASIN(1/SQRT(5 + 2*SQRT(2)))) =180/PI()*(ASIN(1/2*SQRT(17/(2*(6 + SQRT(2)))))) =180/PI()*(ASIN(1/2*SQRT(17/(6 + SQRT(2))))) =180/PI()*(ACOS(1/SQRT(3*(4 + 2*SQRT(2))))) =180/PI()*(3*PI()/8) =180/PI()*(ACOS(1/SQRT(3*(4 + 2*SQRT(2))))+ACOS(1/SQRT(4 + 2*SQRT(2)))) =135 SM MM
09[5,5,5] =3*SQRT(25 + 10*SQRT(5)) =1/4*(15+7*SQRT(5)) =1/6*(SQRT(3)+SQRT(15)) =1/4*(SQRT(3)+SQRT(15)) =1/4*(3+SQRT(5)) =SQRT(5/8 + 11/(8*SQRT(5))) =180/PI()*(ASIN(2/(SQRT(3) + SQRT(15)))) =60 =180/PI()*(ACOS(SQRT(1/10*(5 - SQRT(5))))) =180/PI()*(2*ACOS(SQRT(1/10*(5 - SQRT(5))))) SS
10[4,6,6] =6*(1 + 2*SQRT(3)) =8*SQRT(2) =3/SQRT(10) =SQRT(5/2) =3/2 =SQRT(2) =SQRT(6)/2 =180/PI()*(ASIN((1/2)/(SQRT(5/2)))) =180/PI()*(ASIN(SQRT(5)/3)) =180/PI()*(ASIN(SQRT(5/6))) =180/PI()*(ACOS(1/3)) =180/PI()*(ACOS(1/SQRT(3))) =180/PI()*(ACOS(1/3)+ACOS(1/SQRT(3))) =180/PI()*(2*ACOS(1/SQRT(3))) SM MM
11[3,5,3,5] =SQRT(30*(10 + 3*SQRT(5) + SQRT(15*(5 + 2*SQRT(5))))) =1/6*(45+17*SQRT(5)) =1/4*SQRT((5 + SQRT(5))*2) =1/2*(1+SQRT(5)) =1/2*SQRT(5 + 2*SQRT(5)) =SQRT(1/6*(7 + 3*SQRT(5))) =SQRT(1 + 2/SQRT(5)) =18 =180/PI()*(ASIN(SQRT(2/(5 + SQRT(5))))) =180/PI()*(ASIN((1 + SQRT(5))/SQRT(2*(5 + SQRT(5))))) =180/PI()*(ACOS(1/SQRT(15 + 6*SQRT(5)))) =180/PI()*(ACOS(1/SQRT(5))) =180/PI()*(PI() - ATAN(3 - SQRT(5))) SM
12[3,8,8] =2*SQRT(3) + 12*(1 + SQRT(2)) =7/3*(3 + 2*SQRT(2)) =1/17*SQRT(34*(5 + 2*SQRT(2))) =1/2*SQRT(7+4*SQRT(2)) =1 + 1/SQRT(2) =SQRT(3)/2 + SQRT(6)/3 =1/2*(1 + SQRT(2)) =180/PI()*(ASIN(1/SQRT(7 + 4*SQRT(2)))) =180/PI()*(ATAN(SQRT(23 - 16*SQRT(2)))) =180/PI()*(ATAN(SQRT(7 + 4*SQRT(2)))) =180/PI()*(ACOS((-1 + SQRT(2))/SQRT(6))) =45 =180/PI()*(PI()/4 + ACOS((-1 + SQRT(2))/SQRT(6))) =90 SM MM
13[3,3,3,3,5] =20*SQRT(3)+15/SQRT(5-2*SQRT(5)) =1/12*(20*SQRT(2*(19+7*SQRT(5)+2^(2/3)*(5112+2285*SQRT(5)-3*SQRT(7137+3192*SQRT(5)))^(1/3)+2^(2/3)*(5112+2285*SQRT(5)+3*SQRT(7137+3192*SQRT(5)))^(1/3)))+SQRT(6*(5+2*SQRT(5))*(75+23*SQRT(5)+5*2^(2/3)*(5112+2285*SQRT(5)-3*SQRT(7137+3192*SQRT(5)))^(1/3)+5*2^(2/3)*(5112+2285*SQRT(5)+3*SQRT(7137+3192*SQRT(5)))^(1/3)))) = 1/SQRT(1254/(580 + 20*SQRT(5) + (2*(6192143 + 2563547*SQRT(5) - 627*SQRT(6*(5760573 + 2813807*SQRT(5)))))^(1/3) + (2*(6192143 + 2563547*SQRT(5) + 627*SQRT(6*(5760573 + 2813807*SQRT(5)))))^(1/3))) =1/12*SQRT(6*(27+7*SQRT(5)+(20448+9140*SQRT(5)-12*SQRT(7137+3192*SQRT(5)))^(1/3)+(20448+9140*SQRT(5)+12*SQRT(7137+3192*SQRT(5)))^(1/3))) =SQRT(1/24*(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140* SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)) - 1/4) =SQRT(1/24*(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)) - 1/3) =SQRT((1/12*SQRT(6*(27+7*SQRT(5)+(20448+9140*SQRT(5)-12*SQRT(7137+3192*SQRT(5)))^(1/3)+(20448+9140*SQRT(5)+12*SQRT(7137+3192*SQRT(5)))^(1/3))))^2-(1/2/SIN(PI()/5))^2) =180/PI()*(ASIN(SQRT(6/(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))) =180/PI()*(ASIN((1/2)/( 1/SQRT(1254/(580 + 20*SQRT(5) + (2*(6192143 + 2563547*SQRT(5) - 627*SQRT(6*(5760573 + 2813807*SQRT(5)))))^(1/3) + (2*(6192143 + 2563547*SQRT(5) + 627*SQRT(6*(5760573 + 2813807*SQRT(5)))))^(1/3)))))) =180/PI()*(ASIN((COS(PI()/5))/( 1/SQRT(1254/(580 + 20*SQRT(5) + (2*(6192143 + 2563547*SQRT(5) - 627*SQRT(6*(5760573 + 2813807*SQRT(5)))))^(1/3) + (2*(6192143 + 2563547*SQRT(5) + 627*SQRT(6*(5760573 + 2813807*SQRT(5)))))^(1/3)))))) =180/PI()*(ACOS((1/2/TAN(PI()/3))/(SQRT(1/24*(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140* SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)) - 1/4)))) =180/PI()*(ACOS((1/2/TAN(PI()/5))/(SQRT(1/24*(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140* SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)) - 1/4)))) =180/PI()*((ACOS((1/2/TAN(PI()/3))/(SQRT(1/24*(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140* SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)) - 1/4))))*2) =180/PI()*(ACOS((1/2/TAN(PI()/3))/(SQRT(1/24*(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140* SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)) - 1/4)))+ACOS((1/2/TAN(PI()/5))/(SQRT(1/24*(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140* SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)) - 1/4)))) SS SM
14[3,4,5,4] =30+SQRT(30*(10+3*SQRT(5)+SQRT(75+30*SQRT(5)))) =20+29*SQRT(5)/3 =SQRT(2/41*(15 + 2*SQRT(5))) =1/2*SQRT(11+4*SQRT(5)) =SQRT(5/2 + SQRT(5)) =SQRT(5/3) + SQRT(3)/2 =1 + SQRT(5)/2 =3/2*SQRT(1 + 2/SQRT(5)) =180/PI()*(ASIN(1/SQRT(11 + 4*SQRT(5)))) =180/PI()*(ASIN(1/2*SQRT(3/2 - 1/SQRT(5)))) =180/PI()*(ATAN(SQRT(19 - 8*SQRT(5)))) =180/PI()*(ASIN(1/4*SQRT(7 + 9/SQRT(5)))) =180/PI()*(ACOS(SQRT(1/30*(5 - 2*SQRT(5))))) =180/PI()*(ACOS(SQRT(1/2 - 1/SQRT(5)))) =180/PI()*(ACOS(1/SQRT(10))) =180/PI()*(PI() - ASIN(SQRT(1/6*(3 - SQRT(5))))) =180/PI()*(ACOS(1/SQRT(10))+ACOS(SQRT(1/2 - 1/SQRT(5)))) SM ML
15[4,6,8] =12*(2+SQRT(2)+SQRT(3)) =22+14*SQRT(2) =SQRT(6/97*(14 + SQRT(2))) =(1/2*SQRT(13+6*SQRT(2))) =SQRT(3/2*(2 + SQRT(2))) =1/2*(3 + SQRT(2)) =1/2*(SQRT(3) + SQRT(6)) =1/2 + SQRT(2) =180/PI()*(ASIN(SQRT(1/97*(13 - 6*SQRT(2))))) =180/PI()*(ASIN(1/2*SQRT(1/6*(14 - SQRT(2))))) =180/PI()*(ATAN(SQRT(15 - 8*SQRT(2)))) =180/PI()*(ASIN(1/2*SQRT(13/6 + SQRT(2)))) =180/PI()*(ACOS(1/2*SQRT(1/3*(2 - SQRT(2))))) =180/PI()*(3*PI()/8) =180/PI()*(ACOS(1/2*SQRT(1/3*(2 + SQRT(2))))) =180/PI()*(ACOS(1/2*SQRT(1/3*(2 - SQRT(2))))+3*PI()/8) =135 =180/PI()*(3*PI()/8+ACOS(1/2*SQRT(1/3*(2 + SQRT(2))))) SM SL ML
16[5,6,6] =3*SQRT(5*(65+2*SQRT(5)+4*SQRT(75+30*SQRT(5)))) =1/4*(125+43*SQRT(5)) =3*SQRT(1/218*(21 + SQRT(5))) =1/4*SQRT(2*(29+9*SQRT(5))) =3/4*(1 + SQRT(5)) =1/2*SQRT(25/2 + 41/(2*SQRT(5))) =1/4*(3*SQRT(3) + SQRT(15)) =180/PI()*(ASIN(SQRT(2/(29 + 9*SQRT(5))))) =180/PI()*(ASIN(SQRT(29/72 + SQRT(5)/8))) =180/PI()*(ASIN(1/2*SQRT(1/6*(21 - SQRT(5))))) =180/PI()*(ACOS(1/3*SQRT(1/10*(5 + SQRT(5))))) =180/PI()*(ACOS(2/(SQRT(3) + SQRT(15)))) =180/PI()*(PI() - ATAN(3 - SQRT(5))) =180/PI()*(2*ACOS(SQRT(1/6*(3 - SQRT(5))))) SM MM
17[3,10,10] =5*(SQRT(3)+6*SQRT(5+2*SQRT(5))) =5/12*(99+47*SQRT(5)) =SQRT(5/122*(17 + 3*SQRT(5))) =1/4*SQRT(74 + 30*SQRT(5)) =1/4*(5 + 3*SQRT(5)) =(9 + 5*SQRT(5))/(4*SQRT(3)) =1/4*SQRT(50 + 22*SQRT(5)) =180/PI()*(ASIN(SQRT(2/(37 + 15*SQRT(5))))) =180/PI()*(ASIN(SQRT(61/(10*(17 + 3*SQRT(5)))))) =180/PI()*(ASIN(1/2*SQRT(1/10*(35 + SQRT(5))))) =180/PI()*(ACOS(SQRT(1/30*(7-3*SQRT(5))))) =180/PI()*(ACOS(SQRT(1/10*(5 - SQRT(5))))) =180/PI()*(PI() -ATAN(3 - SQRT(5))) =180/PI()*(ACOS(SQRT(1/10*(5 - SQRT(5))))*2) SM MM
18[4,6,10] =30*(1+SQRT(2*(4+SQRT(5)+SQRT(15+6*SQRT(5))))) =95+50*SQRT(5) =SQRT(6/241*(35 + 2*SQRT(5))) =(1/2*SQRT(31+12*SQRT(5))) =1/2*SQRT(6*(5 + 2*SQRT(5))) =3/2 + SQRT(5) =SQRT(3) + SQRT(15)/2 =1/2*SQRT(25 + 10 *SQRT(5)) =180/PI()*(ASIN(1/SQRT(31 + 12*SQRT(5)))) =180/PI()*(ASIN(1/2*SQRT(7/3 - 2/(3*SQRT(5))))) =180/PI()*(ASIN(1/2*SQRT(1/10*(35 - 2*SQRT(5))))) =180/PI()*(ATAN(SQRT(31/5 + 12/SQRT(5)))) =180/PI()*(ACOS(SQRT(1/30*(5-2*SQRT(5))))) =180/PI()*(ACOS(SQRT(1/2 - 1/SQRT(5)))) =180/PI()*(ACOS(1/SQRT(6))) =180/PI()*(PI()- ASIN(SQRT(1/6*(3 - SQRT(5))))) =180/PI()*(ACOS(SQRT(1/30*(5-2*SQRT(5))))+ACOS(1/SQRT(6))) =180/PI()*(PI()-ATAN(3-SQRT(5))) SM SL ML
名称 面積 体積 稜芯寸 双面芯寸 頂芯寸S 頂芯寸M 頂芯寸L 双稜寸S 双稜寸M 双稜寸L 稜寸結S 稜寸結M 稜寸結L 二面角 仰角S 仰角M 仰角L a稜開角/2 b稜開角/2 c稜開角/2 a 稜寸 / 稜芯寸 b 稜寸 / 稜芯寸 c 稜寸 / 稜芯寸 面積2 体積2
01双[3,3,3] =SQRT(3) =1/12*SQRT(2) =1/4*SQRT(2) =1/12*SQRT(6) =1/4*SQRT(6) =1/2 =1 =360/PI()*ATAN(1/SQRT(2)) =180/PI()* ATAN(SQRT(2)) =30 =SQRT(2) =SQRT(3) =1/12*SQRT(2)
02双[3,3,3,3] =3 =1/4*SQRT(2) =1/2 =1/4*SQRT(2) =1/4*SQRT(6) =1/4*SQRT(2) =1/2*SQRT(2) =90 =180/PI()*ATAN(1/SQRT(2)) =45 =1/2*SQRT(2) =6 =1
03双[4,4,4] =4* SQRT(3) =4/3 =(1/2*SQRT(2)) =(1/3*SQRT(3)) =1 =1/2*SQRT(2) =SQRT(2) =360/PI()*ATAN(SQRT(2)) =45 =30 =1 =2* SQRT(3) =1/3*SQRT(2)
04双[3,3,3,3,3] =15*SQRT(2/(5 + SQRT(5))) =1/4*(5 + SQRT(5)) =1/4*(1 + SQRT(5)) =1/2*SQRT(1 + 2/SQRT(5)) =1/2*SQRT(3) =SQRT((1/2*SQRT(3))^2-(1/4*(1 + SQRT(5)))^2) =1/2*(-1 + SQRT(5)) =360/PI()*ATAN(1/2*(1+SQRT(5))) =180/PI()*ATAN(2/(3 + SQRT(5))) =54 =1/2*(3 - SQRT(5)) =3*SQRT(25 + 10*SQRT(5)) =1/4*(15 + 7*SQRT(5))
05双[3,4,3,4] =27/4*SQRT(2) =27/16*SQRT(2) =SQRT(1-(1/2)^2) =3/4 =3/8*SQRT(6) =3/4*SQRT(2) =1/8*SQRT(6) =1/4*SQRT(6) =3/8*SQRT(6) =360/3 =90-(180/PI()*ACOS(1/3)) =180/PI()*ASIN(1/SQRT(3)) =180/PI()*ATAN(SQRT(2)) =180/PI()*ATAN(1/SQRT(2)) =1/4*SQRT(2) =1/2*SQRT(2) =8*SQRT(2) =1/9*16*SQRT(3)
06双[3,6,6] =27/5*SQRT(11) =81/20*SQRT(2) =3/4*SQRT(2) =9/44*SQRT(22) =9/20*SQRT(6) =3/4*SQRT(6) =3/10 =3/2 =9/5 =3 =360/PI()*ATAN(3/SQRT(2)) =180/PI()* ATAN(SQRT(2)/5) =180/PI()*ATAN(SQRT(2)) =180/PI()*ASIN(5/6) =180/PI()*ASIN(1/(2*SQRT(3))) =1/5*SQRT(2) =SQRT(2) =5/3*SQRT(11) =25/36*SQRT(2)
07双[3,3,3,3,4] =SQRT(6*(2501-363*SQRT(33))^(1/3)+6*(2501+363*SQRT(33))^(1/3)+228) =1/6*SQRT(678 + 6*(1327067 - 1419*SQRT(33))^(1/3) + 6*(1327067 + 1419*SQRT(33))^(1/3)) =1/(2*SQRT(3/(7 + (199 - 3*SQRT(33))^(1/3) + (199 + 3*SQRT(33))^(1/3)))) =1/(2*SQRT(42/(78 + (66*(6039 - 49*SQRT(33)))^(1/3) + (66*(6039 + 49*SQRT(33)))^(1/3)))) =1/(2*SQRT(2/(6 + (6*(9 - SQRT(33)))^(1/3) + (6 *(9 + SQRT(33)))^(1/3)))) =1/(2*SQRT(6/(14 + (2*(1777 - 33*SQRT(33)))^(1/3) + (2*(1777 + 33*SQRT(33)))^(1/3)))) =1/(2*(3*SQRT(33) - 13)^(1/6)*SQRT(6/(4*(3*SQRT(33) - 13)^(1/3) + 2^(1/3)*(3*SQRT(33) - 13)^(2/3) - 4*2^(2/3)))) =1/(2*SQRT(6/((6*(9 - SQRT(33)))^(1/3) + (6*(9 + SQRT(33)))^(1/3)))) =1/6*SQRT(24 - (24*2^(2/3))/(-13 + 3*SQRT(33))^(1/3) + 6*(-26 + 6*SQRT(33))^(1/3)) =1/(2*SQRT(3/(4 + (19 - 3*SQRT(33))^(1/3) + (19 + 3*SQRT(33))^(1/3)))) =360/PI()*ASIN(3/SQRT(24 - 3*(19 - 3*SQRT(33))^(1/3) - 3*(19 + 3*SQRT(33))^(1/3))) =180/PI()*ASIN(1/SQRT(7 + (199 - 3*SQRT(33))^(1/3) + (199 + 3*SQRT(33))^(1/3))) =180/PI()*ASIN(SQRT(3/(7 + (199 - 3*SQRT(33))^(1/3) + (199 + 3*SQRT(33))^(1/3)))) =180/PI()* ASIN(1/(2*SQRT(3/(4 + (19 - 3*SQRT(33))^(1/3) + (19 + 3*SQRT(33))^(1/3))))) =180/PI()*ASIN(SQRT(3/((54 - 6*SQRT(33))^(1/3) + (6*(9 + SQRT(33)))^(1/3)))) =1/SQRT(2/(2 - (4*2^(2/3))/(-13 + 3*SQRT(33))^(1/3) + (2*(-13 + 3*SQRT(33)))^(1/3))) =1/6*SQRT(-36 + 6*(54 - 6*SQRT(33))^(1/3) + 6*(54 + 6*SQRT(33))^(1/3)) =2*SQRT(3*(85 + (570862 - 19074*SQRT(33))^(1/3) + (570862 + 19074*SQRT(33))^(1/3))) =1/3*SQRT(3*(2047255857 - 252417*SQRT(33))^(1/3) + 3*(2047255857 + 252417*SQRT(33))^(1/3) + 3807)
08双[3,4,4,4] =24/7*SQRT(62 - 16*SQRT(2)) =16/7*(1 + 2*SQRT(2)) =SQRT(1 + 1/SQRT(2)) =SQRT(2/17*(7 + 4*SQRT(2))) =1/7*(4*SQRT(3) + SQRT(6)) =SQRT(2) =1/7*SQRT(5 - 1/SQRT(2)) =SQRT(1 - 1/SQRT(2)) =2/7*SQRT(10 - SQRT(2)) =SQRT(4 - 2*SQRT(2)) =360/PI()*ATAN(SQRT(2*(2 + SQRT(2)))) =90 - 180/PI()*ACOS(1/SQRT(6*(2 + SQRT(2)))) =90-135/2 =180/PI()*ASIN(SQRT(10 + SQRT(2))/4) =180/PI()*ASIN(1/2*SQRT(1 + 1/SQRT(2))) =1/7*(3 - SQRT(2)) =SQRT(2) - 1 =6*SQRT(29 - 2*SQRT(2)) =SQRT(122 + 71*SQRT(2))
09双[5,5,5] =5/2*(3*SQRT(3)+SQRT(15)) =5/12*(11 + 5*SQRT(5)) =1/4*(3 + SQRT(5)) =(2 + SQRT(5))/(2*SQRT(3)) =1/2*SQRT(5 + 2*SQRT(5)) =1/4*(1 + SQRT(5)) =1/2*(1 + SQRT(5)) =360/PI()*ATAN(1/2*(3 + SQRT(5))) =90-180/PI()*ACOS(SQRT(1/10*(5 - SQRT(5)))) =30 =1/2*(SQRT(5) - 1) =5*SQRT(3) =5/12*(3 + SQRT(5))
10双[4,6,6] =27/2*SQRT(5) =81/8*SQRT(2) =3/2 =9/20*SQRT(10) =9/8*(SQRT(2)) =3/4*(SQRT(6)) =3/8*SQRT(2) =3/4*SQRT(2) =9/8*SQRT(2) =3/2*SQRT(2) =360/PI()*ATAN(3) =180/PI()*ASIN(1/3) =180/PI()*ASIN(1/SQRT(3)) =180/PI()*ASIN(2/3) =180/PI()*ASIN(1/SQRT(6)) =1/4*SQRT(2) =1/2*SQRT(2) =16/3*SQRT(5) =32/9
11双[3,5,3,5] =75/8*(1 + SQRT(5)) =25/16*(5 + 2*SQRT(5)) =1/2*SQRT(5 + 2*SQRT(5)) =1/8*(5 + 3*SQRT(5)) =1/8*SQRT(3)*(5 + SQRT(5)) =1/4*SQRT(25 + 10*SQRT(5)) =1/4*SQRT(1/2*(5 - SQRT(5))) =1/4*SQRT(5 + 2*SQRT(5)) =1/8*SQRT(10*(5 + SQRT(5))) =360*2/5 =180/PI()*ASIN(1/SQRT(15 + 6*SQRT(5))) =180/PI()*ATAN(1/2) =180/PI()*ATAN(1/2*(1+SQRT(5))) =180/PI()*ASIN(SQRT(1/10*(5 - SQRT(5)))) =1/4*(3 - SQRT(5)) =1/2 =12*SQRT(5) =4*SQRT(5 + 2*SQRT(5))
12双[3,8,8] =12*SQRT(7 + 4*SQRT(2)) =12 + 8*SQRT(2) =1/2*(2 + SQRT(2)) =SQRT(1/17*(23 + 16*SQRT(2))) =SQRT(3) =1 + SQRT(2) =1/2*(2 - SQRT(2)) =1/2*(2 + SQRT(2)) =2 =2+SQRT(2) =360/PI()*ATAN(2+SQRT(2)) =180/PI()*ATAN(3 - 2*SQRT(2)) =45 =180/PI()*ASIN(1/(2*(2 - SQRT(2)))) =180/PI()*ASIN(1/2*SQRT(1 - 1/SQRT(2))) =3 - 2*SQRT(2) =1 =3*SQRT(7+4*SQRT(2)) =3/2 + SQRT(2)
13双[3,3,3,3,5] =(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*COS(ACOS(2*SQRT(2/(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*(1/4)*240+(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(30/(75 + 23*SQRT(5) + 5*2^(2/3)*(5112 + 2285*SQRT(5) - 3*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 5*2^(2/3)*(5112 + 2285*SQRT(5) + 3*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*COS(ACOS(2*SQRT((3*(5 + SQRT(5)))/(5*(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))))))*(1/8*(1 + SQRT(5)))*60 =((((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*COS(ACOS(2*SQRT(2/(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*(1/4)*240)*(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*SIN(ACOS(2*SQRT(2/(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))/3+((((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(30/(75 + 23*SQRT(5) + 5*2^(2/3)*(5112 + 2285*SQRT(5) - 3*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 5*2^(2/3)*(5112 + 2285*SQRT(5) + 3*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*COS(ACOS(2*SQRT((3*(5 + SQRT(5)))/(5*(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))))))*(1/8*(1 + SQRT(5)))*60)*(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*SIN(ACOS(2*SQRT(2/(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))/3 =1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)) =((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*SIN(ACOS(2*SQRT(2/(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))) =(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))) =(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(30/(75 + 23*SQRT(5) + 5*2^(2/3)*(5112 + 2285*SQRT(5) - 3*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 5*2^(2/3)*(5112 + 2285*SQRT(5) + 3*SQRT(7137 + 3192*SQRT(5)))^(1/3))))) =SQRT(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))^2-(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2) =SQRT(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(30/(75 + 23*SQRT(5) + 5*2^(2/3)*(5112 + 2285*SQRT(5) - 3*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 5*2^(2/3)*(5112 + 2285*SQRT(5) + 3*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))^2-(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2) =SQRT(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))^2-(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2)*2 =SQRT(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))^2-(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2)+SQRT(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(30/(75 + 23*SQRT(5) + 5*2^(2/3)*(5112 + 2285*SQRT(5) - 3*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 5*2^(2/3)*(5112 + 2285*SQRT(5) + 3*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))^2-(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2) =180/PI()*(ASIN((1/4)/((1/4)*2*COS(ASIN((1/4)/((1/6*SQRT(3))*(1/12*SQRT(((-12*SQRT(3*(2379 + 1064*SQRT(5))) + 9140*SQRT(5) + 20448)^(1/3) + 7*SQRT(5) + (12*SQRT(3*(2379 + 1064*SQRT(5))) + 9140* SQRT(5) + 20448)^(1/3) + 21)*6))/(1/12*SQRT(114 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))))*2) =90-(180/PI()*ACOS(2*SQRT(3/(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))) =90-(180/PI()*(ACOS(((1/2*SQRT(1 + 2/SQRT(5))))/(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))))) =180/PI()*(ASIN((1/4)/(SQRT(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))^2-(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2)))) =180/PI()*(ASIN(1/8*(1 + SQRT(5))/(SQRT(((1/12*SQRT(126+42*SQRT(5)+6*(20448+9140*SQRT(5)-12*SQRT(7137+3192*SQRT(5)))^(1/3)+6*(20448+9140*SQRT(5)+12*SQRT(7137+3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(30/(75+23*SQRT(5)+5*2^(2/3)*(5112+2285*SQRT(5)-3*SQRT(7137+3192*SQRT(5)))^(1/3)+5*2^(2/3)*(5112+2285*SQRT(5)+3*SQRT(7137+3192*SQRT(5)))^(1/3))))))^2-(1/12*SQRT(126+42*SQRT(5)+6*(20448+9140*SQRT(5)-12*SQRT(7137+3192*SQRT(5)))^(1/3)+6*(20448+9140*SQRT(5)+12*SQRT(7137+3192*SQRT(5)))^(1/3)))^2)))) =SQRT(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))^2-(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2)/(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))) =(SQRT(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(30/(75 + 23*SQRT(5) + 5*2^(2/3)*(5112 + 2285*SQRT(5) - 3*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 5*2^(2/3)*(5112 + 2285*SQRT(5) + 3*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))^2-(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2))/(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))) =((((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*COS(ACOS(2*SQRT(2/(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*(1/4)*240+(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(30/(75 + 23*SQRT(5) + 5*2^(2/3)*(5112 + 2285*SQRT(5) - 3*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 5*2^(2/3)*(5112 + 2285*SQRT(5) + 3*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*COS(ACOS(2*SQRT((3*(5 + SQRT(5)))/(5*(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))))))*(1/8*(1 + SQRT(5)))*60)/(SQRT(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))^2-(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2)*2)^2 =(((((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*COS(ACOS(2*SQRT(2/(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*(1/4)*240)*(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*SIN(ACOS(2*SQRT(2/(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))/3+((((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(30/(75 + 23*SQRT(5) + 5*2^(2/3)*(5112 + 2285*SQRT(5) - 3*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 5*2^(2/3)*(5112 + 2285*SQRT(5) + 3*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*COS(ACOS(2*SQRT((3*(5 + SQRT(5)))/(5*(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))))))*(1/8*(1 + SQRT(5)))*60)*(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))*SIN(ACOS(2*SQRT(2/(27 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))/3)/(SQRT(((1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2/(1/(2*SQRT(6/(19 + 7*SQRT(5) + (20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + (20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3))))))^2-(1/12*SQRT(126 + 42*SQRT(5) + 6*(20448 + 9140*SQRT(5) - 12*SQRT(7137 + 3192*SQRT(5)))^(1/3) + 6*(20448 + 9140*SQRT(5) + 12*SQRT(7137 + 3192*SQRT(5)))^(1/3)))^2)*2)^3
14双[3,4,5,4] =100/11*SQRT(79 - 16*SQRT(5)) =100/33*(5 + 4*SQRT(5)) =SQRT(5/2 + SQRT(5)) =SQRT(5/41*(19 + 8*SQRT(5))) =1/11*(5 + 4*SQRT(5))*SQRT(3) =SQRT(5) =1/3*SQRT(5*(5+2*SQRT(5))) =1/22*SQRT(50 - 4*SQRT(5)) =SQRT(5/2 - SQRT(5)) =1/3*SQRT(5/2 + SQRT(5)) =1/11*SQRT(425 - 155*SQRT(5)) =1/3*SQRT(25 - 5*SQRT(5)) =360/PI()*ATAN(SQRT(10 + 4*SQRT(5))) =180/PI()*ASIN(SQRT(1/30*(5 - 2*SQRT(5)))) =180/PI()*ASIN(1/SQRT(10 + 4*SQRT(5))) =180/PI()*ASIN(1/SQRT(10)) =180/PI()*ASIN(SQRT(5/8+1/(4*SQRT(5)))) =180/PI()*ASIN(SQRT(1/4 + 1/(2*SQRT(5)))) =180/PI()*ASIN(3/4*SQRT(1 - 1/SQRT(5))) =1/11*(-3 + 2*SQRT(5)) =SQRT(5) - 2 =1/3 =(100/11*SQRT(79 - 16*SQRT(5)))/(1/11*SQRT(425 - 155*SQRT(5)))^2 =1/3*SQRT(29530 + 13204*SQRT(5))
15双[4,6,8] =72/7*SQRT(26 + 12*SQRT(2)) =144/7*(1 + SQRT(2)) =1/2*SQRT(6*(2 + SQRT(2))) =3*SQRT(2/97*(15 + 8*SQRT(2))) =3/7*(4 + SQRT(2)) =SQRT(6) =3/7*(2 + 3*SQRT(2)) =1/14*SQRT(6*(10 - SQRT(2))) =SQRT(3 - 3/SQRT(2)) =1/7*SQRT(51 + 69/SQRT(2)) =2/7*SQRT(30 - 3*SQRT(2)) =3/7*SQRT(12 + 6*SQRT(2)) =2/7*SQRT(60 + 6*SQRT(2)) =360/PI()*ASIN(2*SQRT(3/(14 - SQRT(2)))) =180/PI()*ASIN(1/SQRT(6*(2 + SQRT(2)))) =45/2 =90 - 180/PI()*ACOS(1/2*SQRT(1/3 *(2 + SQRT(2)))) =180/PI()*ASIN(1/2*SQRT(1/6*(10 + SQRT(2)))) =180/PI()*ASIN(SQRT(2 + SQRT(2))/4) =180/PI()*ASIN(1/2*SQRT(1/6*(11 - 6*SQRT(2)))) =1/7*(3 - SQRT(2)) =SQRT(2) - 1 =1/7*(3 + SQRT(2)) =6/7*SQRT(783+436*SQRT(2)) =SQRT(6582/49 + (4539*SQRT(2))/49)
16双[5,6,6] =135/38*SQRT(922 - 210*SQRT(5)) =405/76*(9 + SQRT(5)) =3/4*(1 + SQRT(5)) =9/2*SQRT(1/109*(17 + 6*SQRT(5))) =9/38*SQRT(65 + 22*SQRT(5)) =1/2*(3*SQRT(3)) =3/76*(7 + 5*SQRT(5)) =3/4*(SQRT(5) - 1) =9/19*(2*SQRT(5) - 1) =3/2*(SQRT(5) - 1) =360/PI()* ATAN(3/2*(1 + SQRT(5))) =180/PI()*ASIN(1/3*SQRT(1/10*(5 + SQRT(5)))) =180/PI()*ASIN((-1 + SQRT(5))/(2*SQRT(3))) =180/PI()*ASIN(1/12*(9 - SQRT(5))) =180/PI()*ASIN(1/(SQRT(3)*(-1 + SQRT(5)))) =1/38*(9 + SQRT(5)) =1/2*(3 - SQRT(5)) =5/6*SQRT((421 + 63*SQRT(5))*2) =5/36*(41 + 25*SQRT(5))
17双[3,10,10] =75/22*SQRT(2*(313 + 117*SQRT(5))) =125/44*(19 + 9*SQRT(5)) =1/4*(5 + 3*SQRT(5)) =5/122*SQRT(2501 + 1098*SQRT(5)) =5/22*SQRT(3)*(3 + 2*SQRT(5)) =1/2*SQRT(25 + 10*SQRT(5)) =1/44*(15-SQRT(5)) =1/4*(5 + SQRT(5)) =5/22*(7 + SQRT(5)) =1/2*(5 + SQRT(5)) =360/PI()* ATAN(1/2*(5 + 3*SQRT(5))) =180/PI()*ASIN(SQRT(1/30*(7 - 3*SQRT(5)))) =90-(180/PI()*ACOS(SQRT(1/10*(5-SQRT(5))))) =180/PI()*ASIN(11/(15 - SQRT(5))) =180/PI()*ASIN(1/2*SQRT(1/10*(5 - SQRT(5)))) =1/22*(5*SQRT(5) - 9) =1/2*(SQRT(5) - 1) =3/2*SQRT((173 - 9*SQRT(5))*2) =1/4*(19 + 13*SQRT(5))
18双[4,6,10] =180/11*SQRT(179 - 24*SQRT(5)) =180/11*(5 + 4*SQRT(5)) =1/2*SQRT(30 + 12*SQRT(5)) =3/241*SQRT(46995 + 19280*SQRT(5)) =3/11*(5 + 4*SQRT(5)) =SQRT(15) =3*SQRT(1 + 2/SQRT(5)) =1/22*SQRT(6*(25 - 2*SQRT(5))) =1/2*SQRT(6*(5 - 2*SQRT(5))) =SQRT(3/2 + 3/SQRT(5)) =1/11*SQRT(1275 - 465*SQRT(5)) =3/11*SQRT(39 + 57/SQRT(5)) =2*SQRT(3 - 3/SQRT(5)) =360/PI()*ATAN(SQRT(6*(5 + 2*SQRT(5)))) =180/PI()*ASIN(SQRT(1/30*(5 - 2*SQRT(5)))) =-(180/PI()*ATAN(2 - SQRT(5))) =180/PI()*ATAN(1/SQRT(5)) =180/PI()*ASIN(SQRT(5/12 + 1/(6*SQRT(5)))) =180/PI()*ASIN(SQRT(1/8 + 1/(4*SQRT(5)))) =180/PI()*ASIN(1/4*SQRT(5 - (5*SQRT(5))/3)) =1/11*(-3+2*SQRT(5)) =SQRT(5) - 2 =1/5*SQRT(5) =3/5*SQRT(10*(1257 + 541*SQRT(5))) =1/5*SQRT(88590 + 39612*SQRT(5))
2021年12月13日
下画像はくずまんじゅうです。
指のあとかたをわざと残し こしあんが少し透けて見える
手づくりがこだわりの生菓子です。
帷子ノ辻 (かたびらのつじ) 商店街の小さなお饅頭屋で買いました。
母親の行きつけだった饅頭屋さんで この季節にはきまって買ってくれていました。
以前もお伝えしたことがありますが 家族はこの商店街の近くに住んでいて
今日 数十年ぶりにこの店に訪れ 懐かしいお菓子に出会えたことに大変感激しています。
はっきりと指のかたのついたくず饅頭は 近頃ほとんど目にすることはありません。
いま ダイヤモンド結晶模型について あれやこれやと やっているところです。
15ミリの小さな寸法でも気楽に加工できるようになりました。
以前よりは かなり技術開発はできたとは思っているのですが
まだ 表現がまとまりません。少し時間をください。
ここで 炭素原子のみで出来ているダイヤモンド結晶のイメージについて少し。
このブログではダイヤモンド結晶を4角棒の構造物として表現しています。
他の表現タイプとしては 丸い玉を原子核と見立て
原子核どおしの繋がりを細い棒で表現されていることが多く
私は 少し異質な表わしかたをしているようです。
でも本当は どちらも極めてディフォルメされた表現だといえるのです。
原子とは 原子核の寸法を 1 としたときその 1 万倍の大きさの
モヤッとした電子雲の球体に包まれているというのが
今の量子科学からの概説として耳にする説明です。
電子は粒子として原子核の周りをまわっているのではなく
存在位置がはっきりしない雲状にとりまいているのだとか。
ダイヤモンド結晶は
両手で抱えられる直径1メートルのボールの中心に 1/10 mm の点があり
そのボールが規則的にギッシリ詰め込まれているとイメージできます。
また 原子と我々の用いる寸法との比較として
原子 1個と ゴルフボール 1個の関係は
ゴルフボール 1個と 地球の大きさだと表現されることがよくあります。
2021年7月8日
04[3,3,3,3,3] 07[3,3,3,3,4] 13[3,3,3,3,5] Excel 多面体 諸量
かなり オタクな 計算遊びのつづきです。
前回 [ 3,3,3,3,5 ] の 外接球半径の計算式を Wolfram Alpha 計算知能で 求めました。
今回 その入力の値を (PI/2-PI/5) から (PI/2-PI/4) に変え
[ 3,3,3,3,4 ] の 値として
(ASIN(1/2/(1-0.5^2/X^2)^(1/2)))*8+(ASIN(SIN((PI/2-PI/4))*2/2/(1-0.5^2/X^2)^(1/2)))*2=2*PI
と 入力し Wolfram Alpha →
計算式が表示されました。
Excel や Wolfram の入力用に 変換した式は以下です。
1/(4*SQRT(6/(80+(101888-1536*SQRT(33))^(1/3)+8*(199+3*SQRT(33))^(1/3))))
Wolfram Alpha →
私が 以前ご報告した 計算式は
SQRT(-(21/(2*(-22+(566-42*SQRT(33))^(1/3)+(566+42*SQRT(33))^(1/3))))) でした。
同様に [ 3,3,3,3,3 ] の 値として
その入力の値を (PI/2-PI/4) から (PI/2-PI/3) に変えるとか
すべて 三角形なので
ASIN(1/2/(1-0.5^2/X^2)^(1/2)))*2*5=2*PI にすると
1/2*SQRT(5/2+SQRT(5)/2) が返えってきました。
以前報告の 計算式は
1/2*SQRT(1/2*(5+SQRT(5))) でした。
三種類それぞれ 計算式は異なっていても 計算数値は全てどれもイコールでした。
もう オタクな計算遊びは やめにして
次回のブログは ダイヤモンド結晶模型について載せようかと思っています。
2021年6月6日
かなり オタクな 計算遊びをひとつ。
以前 ラズパイ上で動作する Wolfram 製品の簡易なマセマティカ を用いて
[ 3,3,3,3,5 ] の 外接球半径の計算式を求めたのですが → Raspberry Pi で Mathematica
見つけられず あっさり断念した経緯がありました。
その後 インターネット上で 外接球半径が計算できる式を発見し
その数式を利用させてもらい 現在に至っています。
しかし 前回のブログをきっかけに 考えなおしていると
X の解を求める 二分法の計算式を用いて Wolfram Alpha 計算知能 という
検索できる (https://www.wolframalpha.com/)
フリーの数理処理システムで X の解を得ることができました。
Wolfram の マセマティカ と同じ ロジックで 処理がなされています。
(ASIN(1/2/(1-0.5^2/X^2)^(1/2)))*8+(ASIN(SIN((PI/2-PI/5))*2/2/(1-0.5^2/X^2)^(1/2)))*2=2*PI
と 入力し Wolfram Alpha →
計算式が表示されました。
Excel や Wolfram の入力用に 変換した式は以下です。
SQRT(9/8+7*SQRT(5)/24+1/384*(83755008+37437440*SQRT(5)-16384*SQRT(64233+28728*SQRT(5)))^(1/3)+1/12*(1/2*(5112+2285*SQRT(5)+SQRT(64233+28728*SQRT(5))))^(1/3))
Wolfram Alpha →
2021年6月4日
諸量計算について 幾度かお伝えしていますが
その中で Excel で作った 外接球半径計算の リメイク版を載せておきます。
このワークシートでは 二分法 という計算手法を用いて
プラトン多面体やアルキメデス多面体の 外接球半径すべてが計算できます。
この 二分法という計算方法を使えたことにより
[ 3,3,3,3,4 ] や [ 3,3,3,3,5 ] の外接球半径の計算値が 他資料の参照ではなく
自前で求めることができました。
計算結果が参考資料と合致しており とても嬉しく思ったことを記憶しています。
面が五つある [3,3,3,3,3] [3,3,3,3,4] [3,3,3,3,5] 以外は 以前お伝えしている
ブラーマグプタの公式 ( Brahmagupta’s formula ) で すべて求められます。
以下がその二分法で解く Excel データです。
転記方法は text として A列 1行目に 全範囲を copy and paste してください。
C列の 12行目から C列の 26行目までが入力欄です。
H列の 12行目から H列の 26行目までが その解答数値です。
30行目以下のデータは 計算初期データで
02行目のデータは
42行目データを copy and paste したものです。
a b c d e 基本数 別解
13 [3,3,3,3,5] 3 3 3 3 5 =SQRT(I2^2-0.5^2)/I2 =1/12*SQRT(6*(27+7*SQRT(5)+(20448+9140*SQRT(5)-12*SQRT(7137+3192*SQRT(5)))^(1/3)+(20448+9140*SQRT(5)+12*SQRT(7137+3192*SQRT(5)))^(1/3)))
多角形 角数 開き寸 かど心寸 開き角 頂芯寸
a =C2 =SIN((PI()/2-PI()/C5))*2 =$D$27 =DEGREES(ASIN(D5/2/E5))*2 = IF(F10=360, 1/2/SQRT(1-D27^2),"")
b =D2 =SIN((PI()/2-PI()/C6))*2 =$D$27 =DEGREES(ASIN(D6/2/E6))*2
c =E2 =SIN((PI()/2-PI()/C7))*2 =$D$27 =DEGREES(ASIN(D7/2/E7))*2
d =F2 =IF(C8=0,0,SIN((PI()/2-PI()/C8))*2) =$D$27 =DEGREES(ASIN(D8/2/E8))*2
e =G2 =IF(C9=0,0,SIN((PI()/2-PI()/C9))*2) =$D$27 =DEGREES(ASIN(D9/2/E9))*2
=SUM(F5:F9)
桁 入力 =ASC(H2)&"0"
1 9 =(1/10)^B12*C12 =VALUE(MID($H$11,B12+2,1))
2 7 =(1/10)^B13*C13 =VALUE(MID($H$11,B13+2,1))
3 2 =(1/10)^B14*C14 =VALUE(MID($H$11,B14+2,1))
4 7 =(1/10)^B15*C15 =VALUE(MID($H$11,B15+2,1))
5 3 =(1/10)^B16*C16 =VALUE(MID($H$11,B16+2,1))
6 2 =(1/10)^B17*C17 =VALUE(MID($H$11,B17+2,1))
7 8 =(1/10)^B18*C18 =VALUE(MID($H$11,B18+2,1))
8 5 =(1/10)^B19*C19 =VALUE(MID($H$11,B19+2,1))
9 0 =(1/10)^B20*C20 =VALUE(MID($H$11,B20+2,1))
10 5 =(1/10)^B21*C21 =VALUE(MID($H$11,B21+2,1))
11 6 =(1/10)^B22*C22 =VALUE(MID($H$11,B22+2,1))
12 5 =(1/10)^B23*C23 =VALUE(MID($H$11,B23+2,1))
13 5 =(1/10)^B24*C24 =VALUE(MID($H$11,B24+2,1))
14 9 =(1/10)^B25*C25 =VALUE(MID($H$11,B25+2,1))
15 6 =(1/10)^B26*C26 =VALUE(MID($H$11,B26+2,1))
=SUM(D12:D26)
a b c d e
01 [3,3,3] 3 3 3 =SQRT(I30^2-0.5^2)/I30 =SQRT(3/2)/2
02 [3,3,3,3] 3 3 3 3 =SQRT(I31^2-0.5^2)/I31 =1/SQRT(2)
03 [4,4,4] 4 4 4 =SQRT(I32^2-0.5^2)/I32 =SQRT(3)/2
04 [3,3,3,3,3] 3 3 3 3 3 =SQRT(I33^2-0.5^2)/I33 =1/2*SQRT(1/2*(5+SQRT(5)))
05 [3,4,3,4] 3 4 3 4 =SQRT(I34^2-0.5^2)/I34 =1
06 [3,6,6] 3 6 6 =SQRT(I35^2-0.5^2)/I35 =SQRT(11/2)/2
07 [3,3,3,3,4] 3 3 3 3 4 =SQRT(I36^2-0.5^2)/I36 =SQRT(-(21/(2*(-22+(566-42*SQRT(33))^(1/3)+(566+42*SQRT(33))^(1/3)))))
08 [3,4,4,4] 3 4 4 4 =SQRT(I37^2-0.5^2)/I37 =1/SQRT(4-2/COS(1/2*ACOS(1/4*(2-SQRT(2))))^2)
09 [5,5,5] 5 5 5 =SQRT(I38^2-0.5^2)/I38 =1/2*SQRT(3/2*(3+SQRT(5)))
10 [4,6,6] 4 6 6 =SQRT(I39^2-0.5^2)/I39 =SQRT(5/2)
11 [3,5,3,5] 3 5 3 5 =SQRT(I40^2-0.5^2)/I40 =SQRT(1/2*(3+SQRT(5)))
12 [3,8,8] 3 8 8 =SQRT(I41^2-0.5^2)/I41 =1/2*SQRT(7+4*SQRT(2))
13 [3,3,3,3,5] 3 3 3 3 5 =SQRT(I42^2-0.5^2)/I42 =1/12*SQRT(6*(27+7*SQRT(5)+(20448+9140*SQRT(5)-12*SQRT(7137+3192*SQRT(5)))^(1/3)+(20448+9140*SQRT(5)+12*SQRT(7137+3192*SQRT(5)))^(1/3)))
14 [3,4,5,4] 3 4 5 4 =SQRT(I43^2-0.5^2)/I43 =1/4*(-1+SQRT(5))*SQRT(1/2*(53+23*SQRT(5)))
15 [4,6,8] 4 6 8 =SQRT(I44^2-0.5^2)/I44 =1/2*SQRT(13+6*SQRT(2))
16 [5,6,6] 5 6 6 =SQRT(I45^2-0.5^2)/I45 =1/2*SQRT(1/2*(29+9*SQRT(5)))
17 [3,10,10] 3 10 10 =SQRT(I46^2-0.5^2)/I46 =1/2*SQRT(1/2*(37+15*SQRT(5)))
18 [4,6,10] 4 6 10 =SQRT(I47^2-0.5^2)/I47 =1/2*SQRT(31+12*SQRT(5))
2021年5月30日
コロナヴァイラスに 翻弄される毎日です。
多面体を作っても ディスプレイに関してほとんど お伝えしていませんでした。
映像左は 100円で買った できあいですが モイチ納得できません。
その右は 七角形のフレィムで作った吊るし台です。
竹の四角棒 5×5×100 を左右 64.29°(297/143) でカットし
木工用ボンドで接着しています。
上から吊らさず
横の辺の部分から てぐすで保持しています。
精度よく加工すれば 強度は保てています。
そのフレィムを 90° と 128.6°の かぎ状にそれぞれ接着した
5×10×70 の板棒四本で挟んでいます。
64.29°(297/143) の計算手順は。
360 / 7 = 51.429
180 – 51.429 = 128.57
128.57 / 2 = 64.286
64.286 のタンジェントは 2.0765 / 1
297 / 2.0765 = 約 143
2.0765 / 1 = 約 297 / 143 になります。
2021年5月16日
やっと 春が来たんだという気がしています。
下画像は 今日初めて咲いているのを発見した スミレです。
もう 梅も咲き 河津桜も咲いているのを目にしてはいましたが
私には スミレの花を見ないと 春が来たという実感が持てないのです。
なぜか わかりませんが。
釈迦堂山門石段 2021 2月28日 15:00
下画像は 今年になって作った多面体の作品です それぞれ複数個作っていて その一例です。
材質は 太さ5mm の竹棒です。割りばしではなく 割らずに使える業務用の竹箸で たくさん安価に入手しました。
今年は これを用いて工作をしてゆこうかなと思っています。
新しいやり方の確認をしながら作ったので 製作途中の画像はありません。
製作と 記録の両立は 一人でしていると 困難な場合が多々あります。
2021年2月28日
明けましておめでとうございます。
前回の投稿で『変なパラレルワールドに紛れ込んで 抜け出すことができません。』
と言って 2020年の暗い年から 明るい 2021年を期待して筆をおきました。
でも 新年から大変なことが起こってしまっています。
ワシントンD.C.といえば 州に属していないアメリカ合衆国・連邦政府直轄地。
議事堂のあるキャピトルヒルは
アメリカ建国の象徴的な地域であり その丘を中心として 都市が形成されています。
このアメリカの議事堂での暴動が
統治の脆弱性や混乱の露呈とみなされてしまっています。
今 世界も混乱しています。 それぞれの国ごとに直面する問題に手一杯。
今以上に世界が対峙し熱くなっているときに起こっていたらと考えると
思うことが多く言葉がうまく出てきません。
この話を続けたとしても ありきたりな言葉の羅列が続くと思われそうです。
今まで言ってきたことの連続として 言葉にしたかったのです。
2021年1月8日
下画像は京都市遠景で 真ん中に京都タワーが写っています。
今年 初めて雪が降りました。午後五時ぐらいですが 屋根に少し雪が残っています。
大晦日です。私が撮る風景写真の 今年最後の一枚となりました。
京都タワーがばっちり見えて 私のお気に入りの景色です。
高校生の頃
アポロのロケットはあのタワーより大きいと言って眺めていたのを記憶しています。
アメリカでは月探査の技術開発の最中でした。
奥嵯峨から東山を望む google map→
今年は 米国に対する認識が大きく変わった年でした。
テレビが普及し始めたころのことを思い出します。
アメリカ製のテレビドラマが多く放映されていて
大きな部屋にゆったりとくつろぎ
広いキッチンにある大きな冷蔵庫を開け
でかい紙パックのミルクや
抱えるような容器に入ったアイスクリームを
無造作に取り出す情景が まぶしく見えていました。
アメリカへのあこがれや
羨ましく思う気持ちが膨らんでいった気がします。
そして アポロ11号の成功です
アメリカが偉大な存在であることをつくづく実感させられました。
でも 今はゲーデルの気分です。
1947年12月5日、前世紀で最も偉大な数学者と呼ばれた
クルト・ゲーデルが
アメリカの市民権を得るために受けた聴聞会で伝えようとしたことがあります。
合衆国憲法に矛盾を見つけた。
それは合衆国を独裁政権に変えることを可能にするだろう。
という内容です。
合衆国憲法の理解度確認の質問を想定し 憲法をディープラーニングしたそうです。
その時同席していたアインシュタインを大いにハラハラさせたとのこと。
幸運な状況であったりで 事なきを得て市民権は得られたそうです。
どの条文が論拠になったとかの情報は何も残っておらす単なる伝説です。
でも 今の私はゲーデル気分です。
変なパラレルワールドに紛れ込んだ気分で 抜け出すことができません。
来年は 良い年でありますようにと 心から望む気持ちでいっぱいです。
2020年12月31日
05[3,4,3,4] Excel ダイヤモンド結晶 多面体 未分類 製作道具
退院してのちの 初めてのブログです。
『絶筆』のエピソードで始まるブログに いつまでもしておけないと思い やっと筆をとることにしました。
病変組織は 膵臓系でした。でも 年相応の元気で 日々を送っています。
毎日 妻との散歩を楽しみ 5000 から 10000 時には 20000の歩数になることもあります。
一時は シゲくアップしていたのに 今は年に数回の投稿になってしまっています。
得意げに投稿する 話題が なかなか見当たらないのです。
ブログを開始してからお伝えしている従来の製作方法に 現在少し変化のあるものをリストアップしておきます。
既に載せているものも含めてです。
・接着剤は 合成ゴム系ボンドでない水溶性の安全･安心なものを使う。
・合成ゴム系ボンドでは簡単にできた 形状維持を 形状保持部材を作成し行う。
・角度確認に Ａ４の1mm 方眼紙ではなく Ａ４の白紙か 5mm 方眼の用紙を用いる。
・方眼紙枠内の 整数比で角度表現をしていたのを 210か297 を基準とする 0.5ミリ刻みの数の分数とする。
・ドレッサー(精細切削材) を粗目(80番手ぐらい)の紙やすりで作る。
・クレイドル(部材接合部加工の固定治具)を 90度の角度で接合した三角形状の板材で作る。
・電子レンジでの木工について 知見を深め大いに活用していく。
・稜部品接合部分の形状を 3タイプに増やし 立体製作を容易にする。
あれやこれや やり方を変更し 以下の画像が そのように作ったもののアラマシです。
ほとんど 電子レンジの中ををくぐらせています。
[3,4,3,4] の製作の中で いろいろと実験をしていたので そのタイプの作品例が多くあります。
左上ふたつは ダイヤモンド結晶模型ですが その下のジグザグな四角形は 丸棒で同じような形状にしようとしているところです。
邪魔くさくなって 頓挫しています。
初めてこのブログをご覧のかたは 説明が意味不明かもしれませんが 基本的なことは既に説明ずみとして 進めてゆきます。
2020年9月20日
前回のブログで 変な入院患者の自分を吐露してしまいました。
それと整合性のある書き方にいま苦慮しています。
きのう 肺癌の手術を受けました。転移なのかどうかは不明で
組織検査の結果を待っています。１０日ほどかかるそうです。
結構手術に対して平常心で臨めたのですが 今回 少し不安がよぎりました。
全身麻酔の手術で これが６回目です。
ブログは その気分の表れで 能天気な入院患者になってしまいました。
絶筆は明るくいこうと。
絶筆に終わらず 今ここに投稿しています。
きのうの昼に手術 今日の昼歩行訓練。スム－ズなものです。
大変頼りになる医療従事者さんたちの力で
今の自分があるとも強く感じています。
これからも アクセス数に一喜一憂せす 思うことを綴ってゆく
所存です。
2020年6月20日
四つの三角リングの組み物 の完成させ方についてお伝えします。
下画像の 左が
三角リングを三っつ組み合わせた状態です。
この状態で あと三本の棒を挿入し
丸棒を斜めにカットした 楕円形の面をピッタリ三か所合わせれば
右のような状態になります。
言うはやすしで 私もその都度頭が混乱してしまいます。
この画像は 一つのタイプの状態で
三角リングを三っつ組み合わせた状態が 二種類あり
この画像を 鏡で左右をひっくり返して見た状態もあります。
こつとしては
三角リングのかどが 三つ組み合わされた状態で上向きにし
あと一つの三角が水平におさまっている
と 考えるとうまくいきました。
でも 完成見本を見ながらでないと
私はなかなか うまくいきません。
すばやく やつてみたいのですが。
この組物の材質は 竹ばしで
三本 横に並べて 17ミリ強の寸法 長さは53.5ミリほどです。
あることで 今日入院して 検査開始を待っています。 ( コロナ関連では幸いありません)
pcr 検査を受けました。唾液採取でした。結果はまだですが陰性のはずです。
退屈しのぎのために 組み方を考えるのもいいかな と持ってきたのを
ベッドのそばに射す 夕日の明りで撮りました。
2020年6月16日
A4用紙のかどからかどに 斜線を引くと 54.74 度 ( 297 / 210 ) の角度が得られると
何度もお伝えしていますが
この角度と 直角のみで 正十二面体を作ってみました。約5Cm の高さの多面体です。
5×5 の角棒を 長寸方向で 24mmの幅 54.74 度の角度で台形状にカットします。
それを 33個 作ります( 画像では 3個上のほうに 写っています)。
30個は多面体の稜の部材用です。
この33個の部材を 左上にある 治具で 整形します。
24mm の寸法に加工した 一つの部材を基準にして
可能な限り正確(つらいち)に台形に加工します。
その台形を 90度回転させ同様にして 画像のように先の尖った部材にします。
断面 5×10 の板棒を 片側54.74 度 斜めの台形部材(長寸 14mm) 6個
(画像では 5×5 の横に 1個)と 5×5 3個で
v字溝が 三方向に等間隔に下がっている治具をつくります。
この治具で 三つの又にした部材と二つの部材で 家の屋根のようなユニットを 6個作ります。
接着剤が固まり 形状が安定したら
あとは パズル気分で組み合わせ 正十二面体を作ることができます。
私は 利き腕が左なので下のような 54.74 度や 90 度の 整形治具を作っていますが
右利きの方は その点を考慮してください。
2020年6月14日
パラレルワールドの存在有無に対する
真面目で理知的な論議があるそうです。
非現実なことが 実際に起こっているという パラレルワールド
私には 量子論的 ひも理論的で 不可思議な 認識困難なものでした。
でも今のグローバルな現実世界を見てみると
そんな不思議な世界に紛れ込んでしまっているような変な気分です。
欲望と偏見 差別と貧困 君臨と隷属
むき出しの不条理な世界を 様々なメディアを通してまのあたりにしています。
気をとりなおし 工作について少しお話を。
ものを作るとき どんなに正確を期しても
角度や数値を近似値で丸める必要が生じます。
測定とは 離散的なものです。
でもモノづくりで使う 特殊な言い回しで つらいちという言葉があります。
離散的でもなく 近似的な意味も持ちません。
基準となる状態に 認識できる範囲で 完全に一致しているということです。
多面体をうまく作る秘訣は つらいちを意識すべきと思っています。
これは むづかしいスキルではなく 単なるル－ティ－ンな心掛けです。
これからも つらいち意識をもって 多面体づくりなどに関して
お伝えしていこうと 思っています。
2020年5月22日
おひさしぶりです。
コロナヴァイラスに翻弄されている 今日この頃です。
[3,4,3,4] を例として最近私が行っている治具の作り方をお伝えします。
多面体つくりの 参考になれば幸いです。
下の画像は
90度と45度の角度カットと 整形という作業をする 治具と
v字型溝の治具 制作の説明です。
ここで使用している木材は
6 ミリ厚 30 ミリ幅 70 ミリ長の板材と
6 ミリ厚 25 ミリ幅 70 ミリ長の板材
( 30 ミリ幅 の代用可 私は消費量が多く経済性のため )
断面が 5 × 5 で 長さ 50 ミリの棒材と
断面が 5 × 5 で 長さ 25 ミリの棒材
断面が 5 × 10 で 長さ 70 ミリの棒材
( 5 × 5 を 2本合わせても可 )
断面が25 × 25 で 長さ100 ミリの棒材
それに つまようじ です。
左上の 25 × 25 の角材は 80番手の紙やすり 20 × 100 と
5 × 100 のポリプロピレン樹脂の薄板を貼っています。
これは 以前からお伝えしている 切削工具です。
25 ミリ幅の板材に 断面 5 × 10 の 棒材を 45度の角度に
接着させるガイドにしています。
同じように 90度用の治具です。
今までこの用途に 断面 5 × 5 を用いていたのですが
めしつぶでの接着でも強度があるようにと 5 × 10に 変更しています。
この接着では めしつぶ ひとつもいらないくらいです。
これらで 30 ミリ幅の板材を 二等分にカットし接合します。
上画像の下左からの説明です。
棒材で v字形溝をつくるものです。
5 × 5 × 50 の棒材に 5 × 5 × 25 の棒材を接着し
この二つを貼り合わせています。
同寸のかどが 向かい合うようになっています。
画像最下部の左が 完成した治具で そのよこは
5 × 5 × 50 の棒材二本を挟みテ－プで縛っています。
続く左のような v字型溝の治具が作れます。
5 ミリ長の ようじや 棒材で補強し接着しています。
接着部分が固化すれは あと半分の接合は簡単です。
下画像の説明をします。
[3,4,3,4] 用の cradle です。
5 ミリ方眼に罫の入ったＡ4 用紙をクリアファイルにいれています。
必要な角度方向に 部材を固定させるためで 両面テ－プを使っています。
左のＡ4 用紙の斜線の角度は 39.2度 ( 210 / 257 ) です。
短寸のかどから 長寸 257 の部分に 四本引いています。
対称に表示され 正確性が高まります。
左下のようにして
6 ミリ厚 30 ミリ幅 70 ミリ長の板材を二等分します。
右側のＡ4 用紙には かどからかどに 二本の線を引いています。
90度を 35.3度と54.7度に分割しています。
v字溝の方向は 画像では 直線に揃っていないようですが
真上から見ると 用紙の長寸方向と 平行です。
あとは 判じ絵にしておきます。
2020年5月2日
久しぶりの投稿です。
昨年のモットーは『 四角棒で作る 手芸木工を 原点に戻って伝える 』
だったと思っているのですが
年超しせまる今になってもまだ実現していません。
でも 合成ゴム系でない接着剤を用いての 新たな方向に
光が見えてきた気がしています。
ただ 少し難点があり お伝えするのを躊躇していました。
それは 電子レンジを用いる 木工だったからです。
木工用ボンドは 粘性が弱く 完全接着までに時間がかかり 作業性に難があり
その弱点克服や効率アップに 電子レンジを頻繁に活用していました。
木工用ボンドの主成分は 水と酢酸ビニルで 健康被害への心配の少ない物質とは
いわれていますが 機能の向上や安定化のために 様々な薬品が添加されています。
平温での作業ではなく高周波の磁力線を照射し百度以上の蒸気が発生します。
結構頻繁にレンジを使用し 少し 不安を感じながらの作業でした。
『これは 私が 自己責任で 注意点をその都度確認しながら行っているものです。
お勧めしているものではありません。私の責任は回避します。』(2015年10月2日)
とも言っていました。
複数の ボンドメーカに 電子レンジ使用の問題点について問い合わせたところ
そのような状況下での 知見はないとか あいまいな答えしか得られませんでした。
いつまでたっても先に進めないので それではと 方針を変えました。
接着剤に 「めしつぶ」を用いいることにしました。
前回 [ 3,4,3,4 ] と その双対多面体を合体させた複合多面体画像を載せましたが
「めしつぶ」を用いています。
乾燥後の性能は木工用ボンドと比べて接着部分の 弾力性に劣り
振動の激しい治具の制作に用いるには 強度を高める補強が必要な場合もあります。
来年は 木工用ボンドと『電子レンジめしつぶ 』 を併用した
手芸木工をお伝えしたいと思っています。
以下に 少し多めのデ-タを載せておきます。
右端が切れていますが 全範囲コピーで 転記できると思います。
開き接合角 と V切り接合角 の説明をします。
開き接合角は 四角棒を平面上に置いて指定角度に垂直カット
V切り接合角は 四角棒をV字溝に固定して指定角度に垂直カット
詳しいことは 次回にお伝えします。
良いお年を。
| 接合角 | 仰角 | 開き接合角 | 開き仰角 | V切り接合角 | |||||||
| 01 | 01 [3,3,3] | 60.0000 | 171.5 / 297 | 54.7356 | 210 / 297 | 30.3612 | 174 / 297 | 63.4349 | 148.5 / 297 | 22.5 | 123 / 297 |
| 02 | 01 双 [3,3,3] 3 | 60.0000 | 171.5 / 297 | 54.7356 | 210 / 297 | 30.3612 | 174 / 297 | 63.4349 | 148.5 / 297 | 22.5 | 123 / 297 |
| 03 | 02 [3,3,3,3] | 45.0000 | 210 / 210 | 45.0000 | 210 / 210 | 30.3612 | 174 / 297 | 54.7356 | 210 / 297 | 22.5 | 123 / 297 |
| 04 | 02 双 [3,3,3,3] 3 | 60.0000 | 171.5 / 297 | 35.2644 | 210 / 297 | 45.0000 | 210 / 210 | 45.0000 | 210 / 210 | 35.2644 | 210 / 297 |
| 05 | 03 [4,4,4] | 60.0000 | 171.5 / 297 | 35.2644 | 210 / 297 | 45.0000 | 210 / 210 | 45.0000 | 210 / 210 | 35.2644 | 210 / 297 |
| 06 | 03 双 [4,4,4] 4 | 45.0000 | 210 / 210 | 45.0000 | 210 / 210 | 30.3612 | 174 / 297 | 54.7356 | 210 / 297 | 22.5 | 123 / 297 |
| 07 | 04 [3,3,3,3,3] | 36.0000 | 210 / 289 | 31.7175 | 183.5 / 297 | 32.3115 | 188 / 297 | 41.1545 | 210 / 240.5 | 24.0948 | 133 / 297 |
| 08 | 04 双 [3,3,3,3,3] 3 | 60.0000 | 171.5 / 297 | 20.9052 | 113.5 / 297 | 54.7356 | 210 / 297 | 28.3772 | 160.5 / 297 | 45 | 210 / 210 |
| 09 | 05 [3,4,3,4] 3 | 35.2644 | 210 / 297 | 30.0000 | 171.5 / 297 | 32.6118 | 190 / 297 | 39.2315 | 210 / 257 | 24.3429 | 134.5 / 297 |
| 10 | 05 [3,4,3,4] 4 | 54.7356 | 210 / 297 | 30.0000 | 171.5 / 297 | 45.4155 | 210 / 213 | 39.2315 | 210 / 257 | 35.6571 | 210 / 292.5 |
| 11 | 05 双 [3,4,3,4] 3 | 60.0000 | 171.5 / 297 | 19.4712 | 105 / 297 | 55.6664 | 203 / 297 | 26.565 | 148.5 / 297 | 45.993 | 210 / 217.5 |
| 12 | 05 双 [3,4,3,4] 4 | 45.0000 | 210 / 210 | 35.2644 | 210 / 297 | 36.2060 | 210 / 287 | 45.0000 | 210 / 210 | 27.3678 | 153.5 / 297 |
| 13 | 06 [3,6,6] 3 | 33.5573 | 197 / 297 | 25.2394 | 140 / 297 | 33.4824 | 196.5 / 297 | 33.6901 | 198 / 297 | 25.066 | 139 / 297 |
| 14 | 06 [3,6,6] 6 | 73.2213 | 89.5 / 297 | 25.2394 | 140 / 297 | 60.3586 | 169 / 297 | 33.6901 | 198 / 297 | 51.1751 | 210 / 261 |
| 15 | 06 双 [3,6,6] 3 | 60.0000 | 171.5 / 297 | 15.7932 | 84 / 297 | 58.0249 | 185.5 / 297 | 21.8015 | 119 / 297 | 48.5605 | 210 / 238 |
| 16 | 06 双 [3,6,6] 6 | 30.0000 | 171.5 / 297 | 54.7356 | 210 / 297 | 17.7643 | 95 / 297 | 63.4349 | 148.5 / 297 | 12.7644 | 67.5 / 297 |
| 17 | 07 [3,3,3,3,4] 3 | 32.5940 | 190 / 297 | 21.8454 | 119 / 297 | 34.1367 | 201.5 / 297 | 29.5509 | 168.5 / 297 | 25.6134 | 142.5 / 297 |
| 18 | 07 [3,3,3,3,4] 4 | 49.6241 | 210 / 247 | 21.8454 | 119 / 297 | 47.0381 | 210 / 225.5 | 29.5509 | 168.5 / 297 | 37.2091 | 210 / 276.5 |
| 19 | 07 双 [3,3,3,3,4] 3 | 60.0000 | 171.5 / 297 | 13.3827 | 70.5 / 297 | 59.5498 | 174.5 / 297 | 18.5961 | 100 / 297 | 50.2605 | 210 / 252.5 |
| 20 | 07 双 [3,3,3,3,4] 4 | 45.0000 | 210 / 210 | 23.6339 | 130 / 297 | 42.7638 | 210 / 227 | 31.7514 | 184 / 297 | 33.1831 | 194 / 297 |
| 21 | 08 [3,4,4,4] 3 | 32.3684 | 188.5 / 297 | 20.9410 | 113.5 / 297 | 34.3158 | 202.5 / 297 | 28.4221 | 160.5 / 297 | 25.7639 | 143.5 / 297 |
| 22 | 08 [3,4,4,4] 4 | 49.2105 | 210 / 243.5 | 20.9410 | 113.5 / 297 | 47.2658 | 210 / 227.5 | 28.4221 | 160.5 / 297 | 37.4292 | 210 / 274.5 |
| 23 | 08 双 [3,4,4,4] 3 | 60.0000 | 171.5 / 297 | 12.7644 | 67.5 / 297 | 59.9385 | 172 / 297 | 17.7643 | 95 / 297 | 50.699 | 210 / 256.5 |
| 24 | 08 双 [3,4,4,4] 4 | 45.0000 | 210 / 210 | 22.5000 | 123 / 297 | 43.3786 | 210 / 222 | 30.3612 | 174 / 297 | 33.75 | 198.5 / 297 |
| 25 | 09 [5,5,5] | 60.0000 | 171.5 / 297 | 20.9052 | 113.5 / 297 | 54.7356 | 210 / 297 | 28.3772 | 160.5 / 297 | 45 | 210 / 210 |
| 26 | 09 双 [5,5,5] 5 | 36.0000 | 210 / 289 | 31.7175 | 183.5 / 297 | 32.3115 | 188 / 297 | 41.1545 | 210 / 240.5 | 24.0948 | 133 / 297 |
| 27 | 10 [4,6,6] 4 | 48.1897 | 210 / 235 | 18.4349 | 99 / 297 | 47.9379 | 210 / 232.5 | 25.2393 | 140 / 297 | 38.0827 | 210 / 268 |
| 28 | 10 [4,6,6] 6 | 65.9052 | 133 / 297 | 18.4349 | 99 / 297 | 60.3586 | 169 / 297 | 25.2393 | 140 / 297 | 51.1751 | 210 / 261 |
| 29 | 10 双 [4,6,6] 4 | 45.0000 | 210 / 210 | 19.4712 | 105 / 297 | 45.0000 | 210 / 210 | 26.565 | 148.5 / 297 | 35.2644 | 210 / 297 |
| 30 | 10 双 [4,6,6] 6 | 30.0000 | 171.5 / 297 | 35.2644 | 210 / 297 | 26.5650 | 148.5 / 297 | 45.0000 | 210 / 210 | 19.4712 | 105 / 297 |
| 31 | 11 [3,5,3,5] 3 | 31.7175 | 183.5 / 297 | 18.0000 | 96.5 / 297 | 34.9134 | 207.5 / 297 | 24.6791 | 136.5 / 297 | 26.2677 | 146.5 / 297 |
| 32 | 11 [3,5,3,5] 5 | 58.2825 | 183.5 / 297 | 18.0000 | 96.5 / 297 | 55.4231 | 204.5 / 297 | 24.6791 | 136.5 / 297 | 45.7323 | 210 / 215.5 |
| 33 | 11 双 [3,5,3,5] 3 | 60.0000 | 171.5 / 297 | 10.8123 | 56.5 / 297 | 61.1597 | 163.5 / 297 | 15.1144 | 80 / 297 | 52.0897 | 210 / 269.5 |
| 34 | 11 双 [3,5,3,5] 5 | 36.0000 | 210 / 289 | 26.5651 | 148.5 / 297 | 34.7465 | 206 / 297 | 35.2644 | 210 / 297 | 26.1268 | 145.5 / 297 |
| 35 | 12 [3,8,8] 3 | 31.3997 | 181.5 / 297 | 16.3249 | 87 / 297 | 35.2644 | 210 / 297 | 22.4999 | 123 / 297 | 26.5651 | 148.5 / 297 |
| 36 | 12 [3,8,8] 8 | 74.3001 | 83.5 / 297 | 16.3249 | 87 / 297 | 67.5000 | 123 / 297 | 22.4999 | 123 / 297 | 59.6388 | 174 / 297 |
| 37 | 12 双 [3,8,8] 3 | 60.0000 | 171.5 / 297 | 9.7356 | 51 / 297 | 61.8294 | 159 / 297 | 13.6387 | 72 / 297 | 52.8612 | 210 / 277.5 |
| 38 | 12 双 [3,8,8] 8 | 22.5000 | 123 / 297 | 45.0000 | 210 / 210 | 17.7643 | 95 / 297 | 54.7356 | 210 / 297 | 12.7644 | 67.5 / 297 |
| 39 | 13 [3,3,3,3,5] 3 | 30.9317 | 178 / 297 | 13.4106 | 71 / 297 | 35.8954 | 210 / 290 | 18.6336 | 100 / 297 | 27.1021 | 152 / 297 |
| 40 | 13 [3,3,3,3,5] 5 | 56.2732 | 198.5 / 297 | 13.4106 | 71 / 297 | 56.8199 | 194 / 297 | 18.6336 | 100 / 297 | 47.2393 | 210 / 227 |
| 41 | 13 双 [3,3,3,3,5] 3 | 60.0000 | 171.5 / 297 | 7.9123 | 41.5 / 297 | 62.9581 | 151.5 / 297 | 11.1196 | 58.5 / 297 | 54.1752 | 210 / 291 |
| 42 | 13 双 [3,3,3,3,5] 5 | 36.0000 | 210 / 289 | 19.1578 | 103 / 297 | 38.0865 | 210 / 268 | 26.1655 | 146 / 297 | 28.9941 | 164.5 / 297 |
| 43 | 14 [3,4,5,4] 3 | 30.8657 | 177.5 / 297 | 12.9393 | 68 / 297 | 36.0000 | 210 / 289 | 18.0000 | 96.5 / 297 | 27.1915 | 152.5 / 297 |
| 44 | 14 [3,4,5,4] 4 | 46.5129 | 210 / 221.5 | 12.9393 | 68 / 297 | 49.6138 | 210 / 247 | 18.0000 | 96.5 / 297 | 39.7352 | 210 / 252.5 |
| 45 | 14 [3,4,5,4] 5 | 56.1085 | 199.5 / 297 | 12.9393 | 68 / 297 | 56.9826 | 193 / 297 | 18.0000 | 96.5 / 297 | 47.4166 | 210 / 228.5 |
| 46 | 14 双 [3,4,5,4] 3 | 60.0000 | 171.5 / 297 | 7.6226 | 39.5 / 297 | 63.1369 | 150.5 / 297 | 10.7173 | 56 / 297 | 54.3849 | 210 / 293 |
| 47 | 14 双 [3,4,5,4] 4 | 45.0000 | 210 / 210 | 13.2825 | 70 / 297 | 48.2203 | 210 / 235 | 18.4616 | 99 / 297 | 38.3588 | 210 / 265.5 |
| 48 | 14 双 [3,4,5,4] 5 | 36.0000 | 210 / 289 | 18.4349 | 99 / 297 | 38.4020 | 210 / 265 | 25.2393 | 140 / 297 | 29.27 | 166.5 / 297 |
| 49 | 15 [4,6,8] 4 | 46.399 | 210 / 220.5 | 12.4589 | 65.5 / 297 | 49.7734 | 210 / 248.5 | 17.3519 | 93 / 297 | 39.8943 | 210 / 251 |
| 50 | 15 [4,6,8] 6 | 62.4877 | 154.5 / 297 | 12.4589 | 65.5 / 297 | 61.9245 | 158.5 / 297 | 17.3519 | 93 / 297 | 52.9711 | 210 / 278.5 |
| 51 | 15 [4,6,8] 8 | 71.1133 | 101.5 / 297 | 12.4589 | 65.5 / 297 | 68.0024 | 120 / 297 | 17.3519 | 93 / 297 | 60.2602 | 169.5 / 297 |
| 52 | 15 双 [4,6,8] 4 | 45.0000 | 210 / 210 | 12.7644 | 67.5 / 297 | 48.4843 | 210 / 237 | 17.7643 | 95 / 297 | 38.6178 | 210 / 263 |
| 53 | 15 双 [4,6,8] 6 | 30.0000 | 171.5 / 297 | 22.5000 | 123 / 297 | 31.7093 | 183.5 / 297 | 30.3612 | 174 / 297 | 23.5994 | 130 / 297 |
| 54 | 15 双 [4,6,8] 8 | 22.5000 | 123 / 297 | 32.2356 | 187.5 / 297 | 22.0888 | 120.5 / 297 | 41.7268 | 210 / 235.5 | 16.0116 | 85 / 297 |
| 55 | 16 [5,6,6] 5 | 55.6906 | 202.5 / 297 | 11.6407 | 61 / 297 | 57.4487 | 189.5 / 297 | 16.2431 | 86.5 / 297 | 47.9263 | 210 / 232.5 |
| 56 | 16 [5,6,6] 6 | 62.1547 | 157 / 297 | 11.6407 | 61 / 297 | 62.2087 | 156.5 / 297 | 16.2431 | 86.5 / 297 | 53.3008 | 210 / 281.5 |
| 57 | 16 双 [5,6,6] 5 | 36.0000 | 210 / 289 | 16.4722 | 88 / 297 | 39.2489 | 210 / 257 | 22.6929 | 124 / 297 | 30.0154 | 171.5 / 297 |
| 58 | 16 双 [5,6,6] 6 | 30.0000 | 171.5 / 297 | 20.9052 | 113.5 / 297 | 32.3115 | 188 / 297 | 28.3772 | 160.5 / 297 | 24.0948 | 133 / 297 |
| 59 | 17 [3,10,10] 3 | 30.4803 | 175 / 297 | 9.69370 | 50.5 / 297 | 36.7418 | 210 / 281.5 | 13.5811 | 71.5 / 297 | 27.828 | 157 / 297 |
| 60 | 17 [3,10,10] 10 | 74.7598 | 81 / 297 | 9.69370 | 50.5 / 297 | 72.4516 | 94 / 297 | 13.5811 | 71.5 / 297 | 65.9052 | 133 / 297 |
| 61 | 17 双 [3,10,10] 3 | 60.0000 | 171.5 / 297 | 5.6599 | 29.5 / 297 | 64.3438 | 142.5 / 297 | 7.9785 | 41.5 / 297 | 55.8123 | 201.5 / 297 |
| 62 | 17 双 [3,10,10] 10 | 18.0000 | 96.5 / 297 | 31.7175 | 183.5 / 297 | 18.4616 | 99 / 297 | 41.1545 | 210 / 240.5 | 13.2825 | 70 / 297 |
| 63 | 18 [4,6,10] 4 | 45.5041 | 210 / 213.5 | 7.55610 | 39.5 / 297 | 51.5274 | 210 / 264.5 | 10.6248 | 55.5 / 297 | 41.6636 | 210 / 236 |
| 64 | 18 [4,6,10] 6 | 60.881 | 165.5 / 297 | 7.55610 | 39.5 / 297 | 63.8432 | 146 / 297 | 10.6248 | 55.5 / 297 | 55.218 | 206.5 / 297 |
| 65 | 18 [4,6,10] 10 | 73.6149 | 87.5 / 297 | 7.55610 | 39.5 / 297 | 73.1153 | 90 / 297 | 10.6248 | 55.5 / 297 | 66.7682 | 127.5 / 297 |
| 66 | 18 双 [4,6,10] 4 | 45.0000 | 210 / 210 | 7.6226 | 39.5 / 297 | 51.0603 | 210 / 260 | 10.7173 | 56 / 297 | 41.1887 | 210 / 240 |
| 67 | 18 双 [4,6,10] 6 | 30.0000 | 171.5 / 297 | 13.2825 | 70 / 297 | 35.0531 | 208.5 / 297 | 18.4616 | 99 / 297 | 26.386 | 147.5 / 297 |
| 68 | 18 双 [4,6,10] 10 | 18.0000 | 96.5 / 297 | 24.0948 | 133 / 297 | 20.3218 | 110 / 297 | 32.3115 | 188 / 297 | 14.6747 | 78 / 297 |
2019年12月30日
