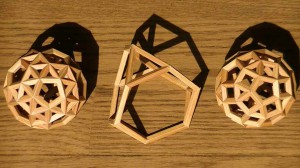RECENT POSTS
06[3,6,6] 多面体 製作道具

[3,6,6] 切頂4面体 Truncated Tetrahedron の製作途中です。
多面体の諸量です。
06 Truncated Tetrahedron 切頂4面体
06 .90453 [3,6,6] 基本数
06 25.239 [3,6,6] 稜の仰角 ( 099/210 )
06 73.221 [3,6,6] 6角形の接合角 ( 199/060 )
06 33.557 [3,6,6] 3角形の接合角 ( 132/199 )
06 1.1726 [3,6,6] 稜寸を 1としたときの頂芯寸 ( 197/168 の比例関係 )
06 1.0607 [3,6,6] 稜寸を 1としたときの稜芯寸 ( 175/165 の比例関係 )
06 .61237 [3,6,6] 稜寸を 1としたときの 6角形の面芯寸 ( 109/178 の比例関係 )
06 1.0206 [3,6,6] 稜寸を 1としたときの 3角形の面芯寸 ( 099/097 の比例関係 )
06 1.6330 [3,6,6] 稜寸を 1としたときの 多面体の高さ
06 12.124 [3,6,6] 稜寸を 1としたときの面積
06 2.7106 [3,6,6] 稜寸を 1としたときの体積
06 [3,6,6] 6角形と 3角形の間の稜の必要個数は 12
06 [3,6,6] 6角形と 6角形の間の稜の必要個数は 06
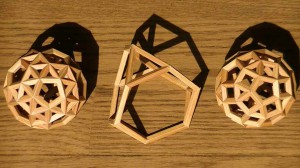
完成です。左は [3,3,3,3,5] 右は [3,4,5,4] です。
高さはどれも 7cmほどです。
多面体を並べて 展示することを考えると、
作品のどんな形状がどんな大きさでうまくバランスが取れるのか、
このことについては いつも考えさせられます。
これはうまくいっていません。
2012年10月27日
13[3,3,3,3,5] Carbon nanotube 多面体

S形の結合部品の組合せ作業のみで迷うことなく簡単に
Pentagonal Hexecontahedron が完成しました。
簡単にとは言っても 稜部品のカットと整形には 飽きるほど単純な反復作業に耐えてきましたが。
次に何をしようかと迷っています。
今までの製作方法の説明と 諸量のデータで 正多面体 準正多面体 双対多面体 そしてそれらの複合多面体 compounds はつくれるはずです。
しかし 私の説明がうまく伝えられていればのことですが。
私自身まだ 作っていない多面体や 複合多面体がありますので
思いつくまま製作して それをお伝えしようかなと 今思っています。
一番最初のブログで お伝えするとしてまだ実行していないものがあります。
それはカーボンナノチューブ (Carbon nanotube) 模型です。
平面充填六角形の円柱座標での取り扱いという単純な作業ではなく。
平面充填三角形のかど点を 三次元の中の円柱面に投影するという説明が必要です。
またその中のタイプの spiral な形状の説明も必要となってきます。
私には大変 困難なことです。少しずつ 準備をしてゆこうと思っています。
球ではなく円柱を取り扱うため symmetry なことではかなり劣りますし。
sashimono としては歪みが生じます。
どれだけ関心のある方たちが居られるかも不安ではあります。
2012年10月21日
13[3,3,3,3,5] 多面体 製作道具

[3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 製作途中です。
左上の四角形の板で作った部品で 三角形の面の上にくる稜の部品をカットします。
その右下の四角形の板で 五角形の面の上にくる稜の部品をカットします。
左端中ほどの 角度の鋭い加工部分のある cradle で五角形の面の上にくる稜部品を整形します。 19.158度の仰角があります。
そしてもう片方の鈍角な加工部分のある cradle で三角形の面の上にくる稜部品を整形します。 7.912度の仰角があります。
寸法の長い 三角形面と五角形面とをまたぐ稜部品はこの二つの cradle をつかいます。
寸法の短い 三角形面と三角形面とをまたぐ稜部品は鈍角な加工部分のある cradle のみをつかいます。
部品は二種類 (3,3形 3,5形) です。
部品を縦方向に置いた場合 以下の形状と個数でず。
三角形をつくる接合面が左右 上下ともにあるもの (3,3形) が 90個必要です。
上下どちらか一端の 左右が 三角形を そしてその反対側の 左右が五角形をつくるもの (3,5形) が 60個必要です。
この[3,3,3,3,5] 双対多面体も鏡像体が存在し 接合作業で混乱が生じる場合があります。
それを回避するための一つの方法が以下です。
元の[3,3,3,3,5] 多面体と同じように 基本的な結合部品があります。
形状が鏡像関係にある結合部品 (N形 S形) があり どちらか一方の部品の集合で多面体が完成します。
画面中ほど上に 小さい部品 (3,3形) 三つでNのような形に接合しそれに長い部品 (3,5形) を二つ結合させた結合部品が N形 です。
画面中央に 小さい部品 (3,3形) 三つでSのような形に接合しそれに長い部品 (3,5形) を二つ結合させた結合部品 (S形) があります。
今回は S形の結合部品の組合せで作業を進めてゆこうとしています。
2012年10月19日
13[3,3,3,3,5] 多面体 製作道具

[3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 製作に必要なもの についてお伝えします。
左のグラフ用紙の上方向にある 三角形の部品は 元の多面体 (変形12面体 Snub Dodecahedron) の 5角形の上にくる稜の仰角をつくる傾斜部品です。その角度は 底辺 213 対辺 074 で表される 斜線をプロットして得られます。
その線に沿って置いてある四角形の板が 90度から仰角を引いた角度 (余角)で稜部品をカットするものです。
10×10 の角材の断面の対角線方向にカットした形状のものを二本貼っています。
左下方向にある 三角形の部品は 元の多面体 (変形12面体 Snub Dodecahedron) の 3角形の上にくる稜の仰角をつくる傾斜部品です。
底辺 223 対辺 031 で表される 斜線をプロットして得られます。
四角形の板はその余角で稜部品をカットするものです。
右のグラフ用紙は [3,3,3,3,5] 双対多面体の稜寸を求めるものです。
二本の勾配を比較して 90度に近い方が 3角形と3角形とをまたぐ稜寸を決めるものです。
双対多面体の面から双対多面体の中芯点までの距離 (面芯寸)を 1としたとき
稜の寸法は 0.2858 になり 対辺 070 底辺 245 でグラフ用紙にその比が得られます。
二つ目の勾配の線が5角形と3角形とをまたぐ稜寸 / 面芯寸 ( 125/250 ) です。
グラフ用紙に載っている二つの部品は 面芯寸が 100mmのときの 稜の部品の寸法になっています。
2012年10月18日
13[3,3,3,3,5] 多面体 製作道具
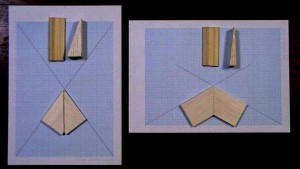
[3,3,3,3,5] 双対多面体の クレィドル cradle の製作中です。
左側のグラフ用紙の上に乗った部品の説明をします。
元の多面体 (変形12面体 Snub Dodecahedron) の
5角形の上にくる稜をつくる cradle です。
接合角は 72度で 左右それぞれ 36度 (360/5/2度 178/245) になります。
その角度は 底辺 245 対辺 178 で表される 斜線を
左右対称にプロットして得られます。
その上方向にある 三角形の部品は
19.158度 (074/213) の仰角をつくる傾斜部品です。
その角度は 底辺 213 対辺 074 で表される 斜線をプロットして得られます。
厚さが 20mm のバルサ材です。
その横にあるのが 巾 30mm の薄板の上に部品を貼ったものです。
10×10 の角材の断面の対角線方向にカットした形状のものを二本貼っています。
対角線方向を下にしています。
右側のグラフ用紙の上に乗った部品の説明をします。
元の多面体 (変形12面体 Snub Dodecahedron) の
3角形の上にくる稜をつくる cradle です。
接合角は 120度で 左右それぞれ 60度 (360/3/2度 194/112) になります。
その角度は 底辺 112 対辺 194 で表される 斜線を
左右対称にプロットして得られます。
その上方向にある 三角形の部品は
7.912度 (031/223) の仰角をつくる傾斜部品です。
その角度は 底辺 223 対辺 031 で表される 斜線をプロットして得られます。
2012年10月17日
13[3,3,3,3,5] 多面体

上は[3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 五角60面体です。
これからつくる製作説明の多面体は 10×10 のバルサ材で
直径20cm の大きさにしようと思っています。
正多面体や準正多面体 の稜寸や仰角は 1種類ですが
双対多面体の稜寸は ほとんど複数あります。
稜寸が1種類でも 仰角は複数あります。
[3,3,3,3,5] 双対多面体は
5角形と3角形の間の稜(3,5形)と 3角形と3角形の間の稜(3,3形) の二種類あります。
もとの多面体[3,3,3,3,5]を基準として以下に諸量の説明をします。
つまりもとの多面体の稜芯寸と こちらの稜芯寸とが同じ値としています。
面芯寸は 2.0399 です。
(3,5形)の稜寸は 1.0200 で 面芯寸との比は 125/250 です。
対辺 125 底辺 250 の比例関係をグラフにプロットしますと
対辺 100mm (作ろうとする多面体の半径) に対する 底辺の実寸は 約50mm になります。
つまり 直径 200mm の (3,5形)の稜寸は 約50mm です。
マザーになる部品の寸法を グラフから決定し それをコピーしながら部品を作ってゆきます。
(3,3形)の稜寸は 0.5829 で 面芯寸との比は 070/245 です。
直径 200mm の (3,3形)の稜寸は 約29mm です。
5角形の上にくる稜の仰角は 19.16度です。
グラフの上に 対辺74 底辺213 で表示できる角度です。
材料カットに必要な 仰角の余角 ( 90 – 19.16 ) もこれから求めます。
3角形の上にくる稜の仰角は 7.91度です。
グラフの上に 対辺31 底辺223 で表示できる角度です。
(3,5形)の稜の必要個数は 60で (3,3形)の稜の必要個数は 90です。
5角形の上にくる稜の接合角は 360 / 5 で 072度なので それぞれ片方が 36度になります。
3角形の上にくる稜の接合角は 360 / 3 で 120度なので それぞれ片方が 60度になります。
今回から 文章の表現方法を変えています。
過去の文章にも 修正を施しました。
英語への自動翻訳を少し意識しています。
以前の多くの文章が自動翻訳では 理解困難だったかもしれません。
2012年10月10日
13[3,3,3,3,5] 多面体

[3,3,3,3,5] の稜の部品加工が終了し 組み立て作業に入っています。
部品は二種類 (3,3形 3,5形) で 部品を縦方向に置いた場合
三角形をつくる接合面が左右 上下ともにあるもの (3,3形) が 90個と
片側 上下が 三角形を そして他の側の上下が五角形をつくるもの (3,5形) が 60個です。
この多面体には鏡像体が存在するため 接合作業で混乱が生じる場合があります。
これを避けるために 今回は一つの方法をとっています。
画面左下のほうに三つの部品 (3,3形) を S状につなげて 二つの部品 (3,5形) を添えているのと
三つの部品 (3,3形) を N状につなげて 二つの部品 (3,5形) を添えているのがありますが
S形に 3,5形二つを結合して 三角形二個つなげた基本結合部品と
N形に 3,5形二つを結合して 三角形二個つなげた基本結合部品との
どちらか一方のみの組合せで多面体 [3,3,3,3,5] が完成します。
今回 N形のほうで結合を進めています。

完成しました。
次回は [3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 五角60面体の
製作手順を お伝えします。
2012年10月9日
13[3,3,3,3,5] 多面体 製作道具

[3,3,3,3,5]準正多面体 の 変形12面体 Snub Dodecahedron の製作部品をつくってゆきます。
作業盆上の四角形の寸法カット用治具は ストッパーもガイドも付けていません。
位置決めのしるしに合わせて ノコギリでカットしてゆくだけです。
作業に慣れや 理解が進めば治具をシンプルにしてゆきます。
10×10 のバルサ材で 14cm の大きさにしようと思っています。
接合面の角度整形をする前の 部品は 1種類で 150個必要です。
仰角 13.411度は グラフ用紙に 対辺 36 底辺 151 の斜線から求め
材料カットに必要な 仰角の余角 ( 90 – 13.411 ) もこれから求めます。
寸法は 三角形の面を底にしたときの高さを 14cm として計算しました。
面芯寸は 2.0771 なので 対辺 243 底辺 117 の比例関係をグラフにプロットし
対辺 70 に対する 底辺の 実寸がその寸法で 約 33.7mm です。
もくもくと ただひたすら カット作業を進めてゆきます。
[3,3,3,3,5] 双対多面体は 10×10 のバルサ材で 20cm の大きさの製作を予定しています。
2012年10月5日
13[3,3,3,3,5] 多面体

今回から [3,3,3,3,5] の多面体とその双対についてお伝えします。
左が [3,3,3,3,5] 変形12面体 Snub Dodecahedron を 5×5の太さのすす竹で表現。
高さは約 70mmです。
右が その双対多面体で Pentagonal Hexecontahedron 五角60面体。
高さは約 105mmです。
どちらの多面体も 鏡面対称の立体が存在します。
多面体の諸量です。
13 変形12面体 Snub Dodecahedron
13 0.9727 [3,3,3,3,5] 基本数
13 13.411 [3,3,3,3,5] 稜の仰角 ( 036/151 )
13 56.273 [3,3,3,3,5] 5角形の接合角 ( 250/167 )
13 30.932 [3,3,3,3,5] 3角形の接合角 ( 148/247 )
13 2.1558 [3,3,3,3,5] 稜寸を 1としたときの頂芯寸 ( 166/077 の比例関係 )
13 2.0971 [3,3,3,3,5] 稜寸を 1としたときの稜芯寸 ( 216/103 の比例関係 )
13 1.9809 [3,3,3,3,5] 稜寸を 1としたときの 5角形の面芯寸 ( 208/105 の比例関係 )
13 2.0771 [3,3,3,3,5] 稜寸を 1としたときの 3角形の面芯寸 ( 243/117 の比例関係 )
13 55.287 [3,3,3,3,5] 稜寸を 1としたときの面積
13 37.617 [3,3,3,3,5] 稜寸を 1としたときの体積
13 [3,3,3,3,5] 5角形と 3角形の間の稜の必要個数は 60
13 [3,3,3,3,5] 3角形と 3角形の間の稜の必要個数は 90
双対の諸量 ( もとの多面体の 稜芯寸と こちらの稜芯寸とが同じ値として)
13 五角60面体 Pentagonal Hexecontahedron
13 2.0399 双対[3,3,3,3,5] 面芯寸
13 2.0971 双対[3,3,3,3,5] 稜芯寸
13 2.2200 双対[3,3,3,3,5] 5角形上の頂芯寸
13 2.1172 双対[3,3,3,3,5] 3角形上の頂芯寸
13 19.158 双対[3,3,3,3,5] 5角形上の稜の仰角 ( 074/213 )
13 7.9123 双対[3,3,3,3,5] 3角形上の稜の仰角 ( 031/223 )
13 36.000 双対[3,3,3,3,5] 5角形上の稜の接合角 ( 180/5度 178/245 )
13 60.000 双対[3,3,3,3,5] 3角形上の稜の接合角 ( 180/3度 194/112 )
13 1.0200 双対[3,3,3,3,5] 5角形と3角形とをまたぐ稜寸
13 0.5829 双対[3,3,3,3,5] 3角形と3角形とをまたぐ稜寸
13 0.5000 双対[3,3,3,3,5] 5角形と3角形とをまたぐ稜寸 / 面芯寸 ( 125/250 )
13 0.2858 双対[3,3,3,3,5] 3角形と3角形とをまたぐ稜寸 / 面芯寸 ( 070/245 )
13 55.281 双対[3,3,3,3,5] 面積
13 37.588 双対[3,3,3,3,5] 体積
13 双対[3,3,3,3,5] 5角形と 3角形の間の稜の必要個数は 60
13 双対[3,3,3,3,5] 3角形と 3角形の間の稜の必要個数は 90
[3,3,3,3,5] の多面体とその双対多面体は 私の最も気に入っている立体の中に含まれます。
2012年10月4日
18[4,6,10] 多面体

[4,6,10] 双対多面体の接合が完了したところです。
まだまだ結合にむらがあり 修正をしてゆきます。
接合面にまだ可塑性が残っているためそれが可能です。
しかし 色々と修正を加えてもシィメトリではない いびつな部分が残ってしまいました。
角度 寸法 加工 等の誤差や 材質のばらつきなどが どうしても発生しています。
いつも誤差との戦いです より完全なシィメトリに強くあこがれます。
2012年10月3日
18[4,6,10] 多面体

[4,6,10] の双対多面体の製作途中です。
三角形が基本の形ですが 鏡面対象の 二種類あります。
前回お伝えした [4,6,10] 多面体と同じく どちらか一つの形状を基本部品として
部分から 中間的形状を作り それらを組合せ 全体的形状に組み立ててゆきます。
接着剤は 透明タイプの合成ゴム系です。
バルサ材は 白っぽいので 透明タイプではないと 接着剤の色が気になることがあります。
合成ゴム系の接着剤は 素早く接着できて 接着面に可塑性がしばらく残り
組み立て作業がスムーズに進みます。
2012年10月2日
18[4,6,10] 多面体 製作道具

10角形と06角形とをまたぐ稜の製作です。
稜寸は 68.93mm です。
左が 10角形の上の稜の形状をつくるクレィドル cradle で
接合角は左右それぞれ 18度 ( 077 / 237 ) 仰角は 24.095度 ( 072/161 ) です。
右が 06角形の上の稜の形状をつくる cradle で
接合角は左右それぞれ 30度 ( 112 / 194 ) 仰角は 13.283度 ( 055/233 ) です。

10角形と04角形とをまたぐ稜の製作です。
稜寸は 58.61mm です。
左が 10角形の上の稜の形状をつくる cradle で
接合角は左右それぞれ 18度 ( 077 / 237 ) 仰角は 24.095度 ( 072/161 ) です。
右が 04角形の上の稜の形状をつくる cradle で
接合角は左右それぞれ 45度 ( 180 / 180 ) 仰角は 7.623度 ( 019/142 ) です。

06角形と04角形とをまたぐ稜の製作です。
稜寸は 37.31mm です。
左が 06角形の上の稜の形状をつくる cradle で
接合角は左右それぞれ 30度 ( 112 / 194 ) 仰角は 13.283度 ( 055/233 ) です。
右が 04角形の上の稜の形状をつくる cradle で
接合角は左右それぞれ 45度 ( 180 / 180 ) 仰角は 7.623度 ( 019/142 ) です。
2012年9月28日
18[4,6,10] 多面体 製作道具

双対 [4,6,10] をつくるための治具や図です。
私は左ききのため画像は 左右反転しています。
今回は 10×10 のバルサ材で 高さ 20cm の大きさに作る予定です。
画面の右の図は 面芯寸 100mm に対する稜の寸法を決定するためのものです。
前回お伝えした 諸量 (下の三行 )をもとにしてグラフ用紙に 図を描いています。
18 0.6893 ( 122 / 177 ) 双対[4,6,10] 10角形と06角形とをまたぐ稜寸 / 面芯寸
18 0.5861 ( 143 / 244 ) 双対[4,6,10] 10角形と04角形とをまたぐ稜寸 / 面芯寸
18 0.3731 ( 075 / 201 ) 双対[4,6,10] 06角形と04角形とをまたぐ稜寸 / 面芯寸
用紙の上に置いている部品の 一番上の寸法の長いのが
10角形と06角形とをまたぐ稜で
面芯寸 100 に対し68.93 であることを 実寸で確認できます。
対辺 122 底辺 177 の傾きの線でこの比例関係が得られます。
上からみて 次の部品は 10角形と04角形とをまたぐ稜寸で
面芯寸 100 に対し 58.61 であることを 実寸で確認できます。
対辺 143 底辺 244 の傾きの線でこの比例関係が得られます。
そして 次の部品は 06角形と04角形とをまたぐ稜寸で
面芯寸 100 に対し 37.31 であることを 実寸で確認できます。
対辺 075 底辺 201 の傾きの線でこの比例関係が得られます。
左側にあるのが 上から 10角形用 6角形用 4角形用 の cradle と
寸法カット用 治具です 以下の諸量をもとにしています。
18 24.094842552110700967 双対[4,6,10] 10角形上の稜の仰角 ( 072/161 )
18 13.282525588538994676 双対[4,6,10] 06角形上の稜の仰角 ( 055/233 )
18 7.6226318593503043571 双対[4,6,10] 04角形上の稜の仰角 ( 019/142 )
18 18.000000000000000000 双対[4,6,10] 10角形上の接合角 ( 180/10度 )
18 30.000000000000000000 双対[4,6,10] 06角形上の接合角 ( 180/06度 )
18 45.000000000000000000 双対[4,6,10] 04角形上の接合角 ( 180/04度 )
18度は 077 / 237 30度は 112 / 194 45度は 180 / 180 で得られます。
2012年9月27日
18[4,6,10] 多面体 諸量

[4,6,10] の双対多面体 六方20面体 Hexakis Icosahedron についてお伝えします。
諸量 ( もとの多面体の稜芯寸と こちらの稜芯寸とが同じ値として)
18 24.094842552110700967 双対[4,6,10] 10角形上の稜の仰角 ( 072/161 )
18 13.282525588538994676 双対[4,6,10] 06角形上の稜の仰角 ( 055/233 )
18 7.6226318593503043571 双対[4,6,10] 04角形上の稜の仰角 ( 019/142 )
18 18.000000000000000000 双対[4,6,10] 10角形上の接合角 ( 180/10度 )
18 30.000000000000000000 双対[4,6,10] 06角形上の接合角 ( 180/06度 )
18 45.000000000000000000 双対[4,6,10] 04角形上の接合角 ( 180/04度 )
18 4.1291457614135206146 双対[4,6,10] 10角形上の頂芯寸
18 3.8729833462074168852 双対[4,6,10] 06角形上の頂芯寸
18 3.8029832481815887597 双対[4,6,10] 04角形上の頂芯寸
18 2.5755459331956214849 双対[4,6,10] 10角形と06角形とをまたぐ稜寸
18 2.1901744798065037825 双対[4,6,10] 10角形と04角形とをまたぐ稜寸
18 1.3942870166557737040 双対[4,6,10] 06角形と04角形とをまたぐ稜寸
18 0.6893 ( 122 / 177 ) 双対[4,6,10] 10角形と06角形とをまたぐ稜寸 / 面芯寸
18 0.5861 ( 143 / 244 ) 双対[4,6,10] 10角形と04角形とをまたぐ稜寸 / 面芯寸
18 0.3731 ( 075 / 201 ) 双対[4,6,10] 06角形と04角形とをまたぐ稜寸 / 面芯寸
18 3.7693771279217166027 双対[4,6,10] 稜芯寸
18 3.7366464560831424485 双対[4,6,10] 面芯寸
18 183.19554518150396045 双対[4,6,10] 面積
18 228.17899489089532558 双対[4,6,10] 体積
18 双対[4,6,10] 10角形と 06角形の間の稜の必要個数は 60
18 双対[4,6,10] 10角形と 04角形の間の稜の必要個数は 60
18 双対[4,6,10] 06角形と 04角形の間の稜の必要個数は 60
双対多面体の名称一覧です。
双対多面体の名称 ( 括弧内は もとの多面体の名称 )
01[3,3,3] Tetrahedron 正4面体
( 正4面体 Tetrahedron )
02[3,3,3,3] Hexahedron 正6面体
( 正8面体 Octahedron )
03[4,4,4] Octahedron 正8面体
( 正6面体 Hexahedron )
04[3,3,3,3,3] Dodecahedron 正12面体
( 正20面体 Icosahedron )
05[3,4,3,4] Rhombic Dodecahedron 菱形12面体
( 立方8面体 Cuboctahedron )
06[3,6,6] Triakis Tetrahedron 三方4面体
( 切頂4面体 Truncated Tetrahedron )
07[3,3,3,3,4] Pentagonal Icositetrahedron 五角24面体
( 変形立方体 Snub Cube )
08[3,4,4,4] Trapezoidal Icositetrahedron 凧形24面体
( 斜方立方8面体 Rhombicuboctahedron )
09[5,5,5] Icosahedron 正20面体
( 正12面体Dodecahedron )
10[4,6,6] Tetrakis Hexahedron 四方6面体
( 切頂8面体Truncated Octahedron )
11[3,5,3,5] Rhombic Triacontahedron 菱形30面体
( 20・12面体Icosidodecahedron )
12[3,8,8] Triakis Octahedron 三方8面体
( 切頂6面体Truncated Hexahedron )
13[3,3,3,3,5] Pentagonal Hexecontahedron 五角60面体
( 変形12面体Snub Dodecahedron)
14[3,4,5,4] Trapezoidal Hexecontahedron 凧形60面体
( 斜方20・12面体Rhombicosidodecahedron )
15[4,6,8] Hexakis Octahedron 六方8面体
( 斜方切頂立方8面体Rhombitruncated Cuboctahedron )
16[5,6,6] Pentakis Dodecahedron 五方12面体
( 切頂20面体Truncated Icosahedron )
17[3,10,10] Triakis Icosahedron 三方20面体
( 切頂12面体Truncated Dodecahedron )
18[4, 6,10] Hexakis Icosahedron 六方20面体
( 斜方切頂20・12面体Rhombitruncated Icosidodecahedron )
2012年9月25日
18[4,6,10] 多面体

[4,6,10] が完成しました 高さは約 20cm です。
Y 字型の基本部品の組合せで 今回は組み立ててゆきました。
基本部品 60組の結合作業のみでは 完成は無理でしたが
ほとんどの結合はこの作業でうまくゆきました。
三種類の部品のあやまった結合をふせげ シィメトリーな状態の維持が容易でした。
[5,6,6] 切頂20面体 Truncated Icosahedron の製作でもお伝えしたとおり
部品の形状の区別に 混乱が生じる場合があります。
正しい組合せ状態の基本部品をもとに製作を行うことで それの回避が容易です。
2012年9月24日
18[4,6,10] 多面体

[4,6,10] の製作中です。
2012年9月22日
18[4,6,10] 多面体

[4,6,10] の製作中です。
Y 字型の 基本部品を二つ合わせて 四角形から対称的に稜がのびている形状を作ったり
その形状を三つ合わせて 四角形が三方から六角形を囲む形状にしたり
部分から 中間的形状を作り それらを組合せ 全体的形状に組み立ててゆきます。
少し話を変えます。
このブログを立ち上げてから 4ヶ月ほど 経過しています。
日本以外の複数の国の方たちからも このブログを見てもらっていることに
驚きと喜びを感じています。
アクセス数はそれほど多くありませんが 日本より 海外のほうが多くあります。
私の日本語の表現が 自動翻訳でどれほど 正確に伝わっているか分かりません。
また 私の説明している内容を日本語で 解釈する場合でも
うまく伝わっているかと 大いに悩むところです。
2012年9月21日
18[4,6,10] 多面体 製作道具

[4,6,10] 製作のクレィドル cradle です。
画面上中は 四角形に接する稜を作る cradle で
左右の接合角がそれぞれ 45.504度 ( 対辺 172 / 底辺 169 の角度 )
仰角が 7.556度 ( 対辺 026 / 底辺 196 の角度 ) になっています。
画面下左は 六角形に接する稜を作る cradle で
左右の接合角がそれぞれ 60.881度( 対辺 228 / 底辺 127 の角度 )
仰角は上と同じく 7.556度 になっています。
画面下右は 十角形に接する稜を作る cradle で
左右の接合角がそれぞれ 73.615度( 対辺 238 / 底辺 070 の角度 )
仰角はこれも同じく 7.556度 になっています。
画面上右は
部品の接合面の加工をする前の 一定の稜寸にカット整形する cradle です。
今回は
10×10 のバルサ材を 29mm の稜寸でカットします ( 完成品の高さは約 20cm )。
カットと整形を この cradle 一つで行っています。
カットの角度は 仰角 7.556度 ( 対辺 026 / 底辺 196 ) の余角
82.444度 ( 対辺 196 / 底辺 026 ) です。

画面下にあるのは 寸法カットし角度整形した部品です 180個必要です。
接合面の加工をする 三種類の部品の説明をします。
画面上左から一つ目の縦状態の部品が 十角形と六角形との間の稜部品。
画面上左から二つ目の縦状態の部品が 六角形と四角形との間の稜部品。
画面上左から三つ目の縦状態の部品が 十角形と四角形との間の稜部品。
画面上右が 三種類の部品を接合したもので。
この組合せ形状 ( 鏡面対称を含めて ) で [4,6,10] の頂を形成します。
私は この組合せ形状 ( 鏡面対称を含めず ) を 60個を作り
それを基本部品として 組み立ててゆこうと思っています。
2012年9月20日
18[4,6,10] 多面体 諸量

[4,6,10] 斜方切頂20・12面体 を説明します。
私のブログでは 正・準正多面体 の種類を 18としていますが
頂芯寸を 1 としたときの 稜芯寸 (基本数) を
小さいほうから並べると 18番目になります。
基本数
01 .5773 [3,3,3] 正4面体 Tetrahedron
02 .7071 [3,3,3,3] 正8面体 Octahedron
03 .8164 [4,4,4] 正6面体 Hexahedron
04 .8506 [3,3,3,3,3] 正20面体 Icosahedron
05 .8660 [3,4,3,4] 立方8面体 Cuboctahedron
06 .9045 [3,6,6] 切頂4面体 Truncated Tetrahedron
07 .9281 [3,3,3,3,4] 変形立方体 Snub Cube
08 .9339 [3,4,4,4] 斜方立方8面体 Rhombicuboctahedron
09 .9341 [5,5,5] 正12面体 Dodecahedron
10 .9486 [4,6,6] 切頂8面体 Truncated Octahedron
11 .9510 [3,5,3,5] 20・12面体 Icosidodecahedron
12 .9596 [3,8,8] 切頂6面体 Truncated Hexahedron
13 .9727 [3,3,3,3,5] 変形12面体 Snub Dodecahedron
14 .9746 [3,4,5,4] 斜方20・12面体 Rhombicosidodecahedron
15 .9764 [4,6,8] 斜方切頂立方8面体 Rhombitruncated Cuboctahedron
16 .9794 [5,6,6] 切頂20面体 Truncated Icosahedron (サッカーボール)
17 .9857 [3,10,10] 切頂12面体 Truncated Dodecahedron
18 斜方切頂20・12面体 Rhombitruncated Icosidodecahedron
18 .99131668954105939137 [4,6,10] 基本数
18 7.5560540461687591650 [4,6,10] 稜の仰角 ( 026/196 )
18 73.614860764356080665 [4,6,10] 10角形の 接合角 ( 238/070 )
18 60.881040189555234516 [4,6,10] 06角形の 接合角 ( 228/127 )
18 45.504099046088684819 [4,6,10] 04角形の 接合角 ( 172/169 )
18 3.8023944998512935848 [4,6,10] 頂芯寸 (稜寸を 1としたとき)
18 3.7693771279217166027 [4,6,10] 稜芯寸 (稜寸を 1としたとき)
18 3.4409548011779338455 [4,6,10] 10角形の面芯寸 (稜寸を 1としたとき)
18 3.6685424806725857361 [4,6,10] 06角形の面芯寸 (稜寸を 1としたとき)
18 3.7360679774997896964 [4,6,10] 04角形の面芯寸 (稜寸を 1としたとき)
18 174.29203034232392088 [4,6,10] 面積 (稜寸を 1としたとき)
18 206.80339887498948482 [4,6,10] 体積 (稜寸を 1としたとき)
18 [4,6,10] 10角形と 06角形の間の稜の必要個数は 60
18 [4,6,10] 10角形と 04角形の間の稜の必要個数は 60
18 [4,6,10] 06角形と 04角形の間の稜の必要個数は 60
2012年9月13日
18[4,6,10] 多面体

右側の多面体が 斜方切頂20・12面体 Rhombitruncated Icosidodecahedron 。
左側の多面体が その双対多面体で 六方20面体 Hexakis Icosahedron と呼ばれています。
名称と形状が 一致しにくいです。
私のブログでは [4,6,10]多面体と [4,6,10]双対多面体と表記しようと思っています。
この画像の [4,6,10]多面体や その双対多面体の高さは約 100mm です。
10年ほど前に作った どちらもプロトタイプで まだまだ sashimono とは呼べない作品です。
これから この二つの多面体製作の説明をしてゆこうと思っています。
2012年9月10日
<
1
2
3
4
5
6
7
8
9
10
11
12
13
>