RECENT POSTS
14[3,4,5,4] Excel 多面体 諸量

斜方20・12面体 [ 3,4,5,4 ] の諸量を エクセルで計算しています。
画像をクリックすると 大きな画面になります。
画像形式が JPGなので 表計算ソフトに文字を移せませんが
最後のほうに記しています文字や計算式を エクセルやそれ相当のソフトに
コピー&ドロップすれば少しは作業性がよくなり走らすことができます。
*注 後日投稿(2015年 05月24日)のリメイク版もあります。そちらをお勧めします。
カラーの背景のセルのみ 数字の手入力部分です。
これで一般的に 正多面体と準正多面体 のデータが計算できます。
左上の 個数 角数の入力欄は 一つの頂に集まる正多角形の 数と角数を入力します。
必ず三行の入力が必要です。
立方八面体[ 3,4,3,4 ]では 三角形が一個と四角形が二個 それにまた三角形が一個と
入力できますが 三角形が二個 四角形が一個 そして四角形が一個でもOKです。
もっとシンプルな体裁にできるのですが IF文を使ったり 式が複雑になります。
もう一つのカラーの背景の 974607762378170 となっている入力欄に
866025403784438の 数字を入れると ←*注
10行目のF列に 360.000000000000000となり
立方八面体[ 3,4,3,4 ] の計算完了で 仰角や接合角がわかります。
計算手順は
個数 角数 個数 角数
1 3 2 3
2 4 1 4
1 3 とか 1 4 などと入力し
最初は 12行目 B列 に 8 を入れ 後のB列はすべてゼロにして
10行目のF列の表示が 360以上の数値になり
7を入れると 今回は計算異常の表示が出ますが 気にせず
その数より 大であるということであり
もとの数字8にもどし つぎの下の 0 を変更します。
ある数字を入れると 360以上になり
その数より1つ上の数を入れると 360以下になる場合
もとの数字にもどし 下の欄の数字の入力をします その繰り返しです。(2015年5月22日 変更)
今までは 天下り的な数値報告をしていましたので
その根拠を伝えたかったのですが
文章が長くなったり 理解しにくい点があるかも知れません お許しください。
コピー&ドロップする内容です
C列からG列までは 書式設定で 小数点以下の桁数を 15にしています。
1 行目 A 列 → 個数
1 行目 B 列 → 角数
1 行目 C 列 → 頂角度(R)
1 行目 D 列 → 頂角度(D)
1 行目 E 列 → 側角度(R)
1 行目 F 列 → 側角度(D)
1 行目 G 列 → 角底寸/2
2 行目 C 列 → =(PI()/2-PI()/B2)*2
2 行目 D 列 → =DEGREES(C2)
2 行目 E 列 → =PI()/B2
2 行目 F 列 → =DEGREES(E2)
2 行目 G 列 → =COS(E2)
2 行目の C 列から G 列まで
セルの右下にポインタを合わせ「+」を
4 行目までドラッグする [オートフィル]機能 を使います。
6 行目 C 列 → 底面 側角度(R)
6 行目 D 列 → 底面 頂角度(R)
6 行目 E 列 → 底面 頂角度(D)
6 行目 F 列 → 底面 総頂角度(D)
6 行目 G 列 → 接合角
7 行目 B 列 → =B2
7 行目 C 列 → =ACOS(G2/$C$27)
7 行目 D 列 → =(PI()/2-C7)*2
7 行目 E 列 → =DEGREES(D7)
7 行目 F 列 → =E7*A2
7 行目 G 列 → =E7/2
7 行目の B 列から G 列まで
セルの右下にポインタを合わせ「+」を
9 行目までドラッグする [オートフィル]機能 を使います。
10 行目 F 列 → =SUM(F7:F9)
12 行目 C 列 → =B12*1/10^A12
12 行目の C 列 の
セルの右下にポインタを合わせ「+」を
26 行目までドラッグする [オートフィル]機能 を使います。
27 行目 C 列 → =SUM(C12:C26)
13 行目 E 列 → 仰角
14 行目 E 列 → =DEGREES(ACOS(C27))
17 行目 E 列 → 稜芯寸
18 行目 E 列 → =0.5*C27/SQRT(1-C27^2)
21 行目 E 列 → 頂芯寸
22 行目 E 列 → =0.5/SQRT(1-C27^2) *2015年3月20日変更
*注
"951056516295153の 数字を入れると" の表現でした (2015年5月22日 まで)
これは 立方八面体[ 3,4,3,4 ] の値ではなく 20・12面体[3,5,3,5] の値でした
混乱をおかけしたことを お詫びし 訂正いたします。
2012年7月9日
05[3,4,3,4] 多面体 製作道具
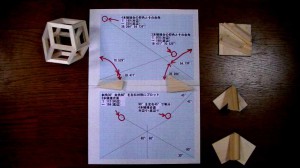
立方八面体[ 3,4,3,4 ] の 双対多面体 菱形十二面体の 製作関連画面です。
双対多面体の製作部品の特徴は 稜線を上下方向に向けたとき
上下両端の接合形状は接合面角度 仰角が異なり 左右形状は同じです。
右上のクレィドルは仰角19.471度の余角70.529度の角度で一つの端の整形面をつくり
もう一端を仰角35.264度の余角54.736度の整形面にします。
19.471度 は 対辺 070 底辺 198 35.264度 は 対辺 169 底辺 239。
右中のクレィドルは左右45度の角度で
仰角35.264度の溝に置き 余角54.736度の整形面を垂直にして整形します。
右下のクレィドルは左右60度の角度で
仰角19.471度の溝に置き 余角70.529度の整形面を垂直にして整形します。
多面体の大きさ(高さ)と稜の寸法の関係をお伝えします。
立方八面体の三角形を底にした場合の高さと菱形十二面体の高さを 1 とすると
稜の寸法は 0.612 になります。
立方八面体の四角形を底にした場合 高さ 1 に対し 稜寸は 0.707 です。
24個の部品の同一形状どおしを接合してゆけば あっけなく完成します。

次回は上の画像と同じ斜方20・12面体 [ 3,4,5,4 ]について お伝えしようと思います。
今までとは違って 説明難度が相当高いです。
2012年7月3日
05[3,4,3,4] 多面体 組物 製作道具
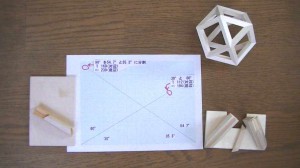
“三角の組み物” と兄弟関係にある立方八面体の 製作関連写真です。
この多面体は 製作2 製作3 でお伝えした 二十・十二面体と同じく
一つの形状の部品で組み立てられ 三角形に組んだ部品の結合でできます。
クレィドルも 傾斜は一つの角度 ( 30°)で
余角の 60°でカットした面を垂直にした部品を
二種類の接合角 (54.7°と35.3°計 90°) になるよう整形し
部品の両端の形状を 二十・十二面体と同じく面対称にして 24個が必要です。
“三角の組み物”と立方八面体が 兄弟関係にあると説明しましたが
組み物や多面体の頂点の位置が 合同になることができ
組み物の部品の太さと長さの比の値を この立方八面体から計算できるからです。
計算方法は説明困難ですが
多面体の三角形の面と中芯点とでできる立体は “正四面体” で
組み物の外周線は正四面体の面に斜めに “接して” います。
これらを条件として計算をしています。
私は 立方八面体を [ 3,4,3,4 ] (さんよん さんよん)と 呼んでいます。
多面体の一つの頂 (ちょう) に集まる多角形の状態を表しています。
形状が判り すっきりしている気がします。
複数の正多角形でできている準正多面体 の名称は
形状を確定するプロセスや いきさつが解かっていないと
意味不明な部分が多く 馴染みにくい気がします。
正四面体は [ 3,3,3 ](さんみっつ) 正六面体は [ 4,4,4 ] (よんみっつ)。
正八面体は [ 3,3,3,3 ] (さんよっつ)正十二面体は [ 5,5,5 ] (ご みっつ)。
正二十面体は [ 3,3,3,3,3 ] (さんいつつ)とも表現できます。
これらはどれも 正多角形が一種類でできていて 正多面体と呼ばれています。
今までにお伝えした 複数の正多角形でてきた準正多面体 は以下です。
二十・十二面体は [ 3,5,3,5 ]
サッカーボールは [ 5,6,6 ]で 切頂二十面体や
フラーレン fullerene とも呼ばれています。
2012年7月2日
組物 製作道具

これが四つの三角リングの組み物の 製作基本図です いたってシンプルです。
この組み物を作る場合必要な条件は 円柱棒の直径が 1 に対し 円柱で作る正三角形の
外周の一辺が 9.1364817520732 (私の計算では) でなければなりません。
それより小さければ 組み合わず 大きすぎれば 組み合わせがゆるんで形状が保てません。
今回 製作見本として 直径 12mmと表示された バルサ材の棒を用いていますが
10本横に並べて寸法を計測すると 123mm でした。
実際の直径は 平均 12.3mm ということです。

写真に 三角形を二個組み合わせたのが二つありますが
面対象に 二種類の組み方があることがわかります。
どちらかの二個組み合わせてできた輪の中に 三番目の三角形の輪を作ります。
これで三個の三角形の組み物ができあがりました。
つぎは 残る三つのパーツを できた組み合わせの中にシィメトリーに挿入すれば
出来上がりです。
その作業はパズルのようで 説明困難です。
部品が正確にできていれば 最後の三つの部品は接着せずとも全体の形状を保ちます。
これは実際に パズルとして遊べます
2012年6月30日
05[3,4,3,4] 多面体 組物

写真右が お伝えしようとしている 四つの三角リングの組み物 です。
その製作用のための図面を作成中ですが それと関連した多面体も
ここ数年作ったこともなく 発表する前に その検証としてバルサ材で作りました。
中ほどのが 立方八面体で 左はその双対多面体の 菱形十二面体です。
2012年6月29日
04[3,3,3,3,3] 09[5,5,5] Compounds 多面体 組物 製作道具
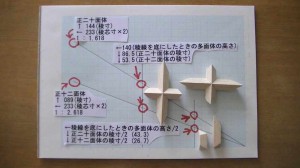
正十二面体と正二十面体との複合多面体 compounds 製作の
基本図面と その部品です。
二つの多面体を複合するには
稜から中芯点までの寸法が同じであることが必要です。
今回寸法を統一して 高さを 140mm とします。

部品の結合作業中です。

完成です この複合多面体は私にとって プロトタイプです。
すす竹では 作ろうという元気が起こりませんでした。

次回は 四つの三角リングでつくる シィメトリーな組み物を お伝えします。
準正多面体 の立法八面体とは兄弟関係にあります。
この組み物はよく目にするのですが どう呼ばれているのか知りません。
2012年6月25日
04[3,3,3,3,3] 09[5,5,5] 多面体 製作道具
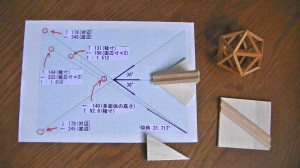
正二十面体製作の基本図面と クレィドルです。
対辺 178 底辺 245 の斜線を 上下対称に二本引きます。
両サイド 36度の接合面をつくるクレィドルを この角度に合せ作成します。
対辺 144 底辺 233 を示す斜線を引きます。
1 対 1.618 の比率を表し 稜寸 1 に対し 稜線から 多面体の中芯点までの寸法の二倍を表示。
そして底辺と斜辺でできる角度は クレィドルの傾き(仰角) 31.717度になります。
もう一本斜線を引きます。
対辺 131 底辺 198 で 1 対 1.512 の比率を表し 稜寸 1 に対し 面芯寸の二倍を示します。
今回も 他の多面体と寸法を合わせるため 高さ 140mm と決定すると
その稜寸が 底辺 140のところの 対辺の実寸として得られます (92.6)。

左のクレィドルで 仰角の余角 58.283 で角材を 寸法をあわせカットし そして整形。
右のクレィドルは 傾き 31.717度の V型溝に 58.283度に面をカットした角材をのせ
面を垂直にして接合面が左右 36度になるように整形します。
この部品を ひたすら 30個と少しの予備として作ってゆきます。
今回画面に載せているのこぎりが 以前のと違っていますが どれも細密加工用ののこぎりです。

完成しました これで正多面体の全種類ができました。
2012年6月23日
04[3,3,3,3,3] 09[5,5,5] 多面体 製作道具
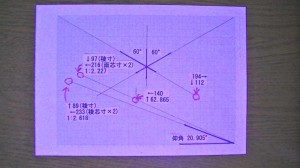
正十二面体を製作するための 基本図面です。
底辺 194 対辺 112 の斜線を 左右対称に 二本書き 接合角左右60度 のクレィドル用と
底辺 233 対辺 089 の比を表す斜線を引きます。
これは 正十二面体の稜寸を 1 としたとき 稜から芯のまでの 二倍の寸法をあらわし
それと 斜辺と底辺とでできる角度が クレィドルの仰角になっています。
この斜線のうえの斜線は 稜寸を 1 としたとき 五角形の面を底にしたときの
多面体の高さを表示する 比例関係の斜線です ( 1 対 2.227)。
今回 140mmの高さの多面体をつくろうとしていますが
底辺 140としたときの 対辺が実寸(62.9)の 稜の寸法になります。

製作途中です。

完成です (稜寸 62.9mm 高さ140mm)。
2012年6月22日
04[3,3,3,3,3] 09[5,5,5] 多面体

正十二面体と正二十面体で 5×5のすす竹 高さは 7cm です。
レオナルドスタイルの工作を始めたきっかけになった 多面体です。
これらも プロトタイプで 1点ものです。
これから 10×10のバルサ材で製作方法をお伝えしてゆきたいと思っています。
2012年6月19日
02[3,3,3,3] 03[4,4,4] Compounds 多面体 製作道具

今日は正八面体( Octahedron ) についてお伝えします
左にあるのがその完成品です。
二つの治具で加工ができます。
今回も 10×10のバルサ材を使用しています ( 寸法は 85mm)。
右端の治具で ( 角棒の直角の面をそれぞれ45度傾ける溝があり 傾斜はなし)
角棒を両端とも45度斜めにカットします。
カットされた面を見ると菱形になっています (両端のカット面は 面対象)。
そして 真ん中のクレィドル cradle で
45度斜めにカットした部品の面を垂直にし(角棒の傾斜は45度)
左右45度ずつ 90度の接合面をつくります。
下の部品のように 右の状態から 左の状態に加工し 12個つくります。
それを接着すれば あっけなく完成です。
部品数も少なく 作業も容易に見えますが 加工角度が鋭角なため
作業性を高めるために ドレサー dresser だけでなく
カッターやのこぎりで ラフ整形をします。
dresser だけの加工では
かなりの 細かい木屑が発生し まめなクリーニングが必要です。
これは レオナルドスタイルの製作のことや この用具だけのことではなく
木材加工全般にもいえることで いつも考慮すべきことです。

正八面体と正六面体の複合多面体 compounds について説明します。
下の図右がその完成品です。
以前 星型八面体の製作をお伝えしたのと同じ方法で 二つの多面体を複合します。
正八面体に対応する部分は 正八面体と同じ寸法の稜寸にしています。
しかし 正六面体は正八面体と形状が異なり
正六面体部分の稜寸を 正八面体と同寸にすると うまく稜が交差しません。
そこで 稜から中芯までの距離をそれぞれ 同じくして複合します。
正八面体の稜寸を 1としたとき 稜芯寸は 0.5 。
正六面体の稜寸を 1としたとき 稜芯寸は 0.707 。
つまり 今回正八面体の稜寸を 85としましたから 高さ85mm で
正六面体の稜寸は 60.1 になります ( 1対 0.707 )。
この比例関係を グラフ用紙に表示すると
底辺 239 (正八面体の稜寸)で 対辺 169 (正六面体の稜寸) の斜線関係となります。

次回は 正十二面体や正二十面体 そしてそれらの複合多面体について
お伝えしようかと 思っています。
2012年6月18日
16[5,6,6] 多面体

五角形面と六角形面のある部品を お互いの 五角形面を接着し
正五角形を形成する部品を12個 つくり
左右に六角形面のある部品を それぞれに ひとつずつ接着します。
この組み合わせた部品を 三つ接合し
六角形のまわりに五角形が三つあるセットを四つ つくります。

六角形のまわりに五角形が三つあるセットを二つ 左右に六角形面のある部品で 連結しました。
同じように 左右に六角形面のある部品で連結してゆきます。
この結合方法は今回この多面体を作る作業で たまたま思い浮かんだ方法です。
色々な方法が考えられます。

完成です 約 18cm の サッカーボール風多面体です。
接着剤は 接着後の少しの時間は接着部に可塑性が残っている合成ゴム系です。
次回は正八面体について そして正六面体と正八面体との
複合多面体 compounds についてもお伝えしようかなと思っています。
2012年6月14日
16[5,6,6] 多面体 製作道具
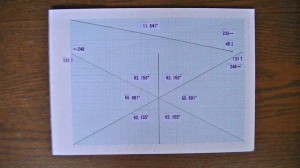
サッカーボル風多面体を製作するための 基本図です( 画面クリックで 拡大図が現れます )。
底辺 248 対辺 131 で 左右対称に斜線を引き 中心に縦線をいれます。
上に 角度 11.641 の 斜線 (底辺 233 対辺 48) をいれます。

62.155度でカットした 板二枚をあわせた クレィドルと
左 62.155度 右 55.691度 の板でつくる クレィドル。
それとは逆に 右 62.155度 左 55.691度 の板でつくる クレィドル
を作ろうとしています。
傾斜は 三つのクレィドルすべて 11.641度 です。

11.641度 の余角 78.359度で 両端をカットし 整形します。
62.155度で 削った部品の面は 六角形をつくり 55.691度は 五角形です。
この多面体に必要な部品は
両端とも左右 62.155度で削ったのが 30個。
稜にそって左右それぞれを見ると 片方両端ともが62.155度で
もう一方が 両端とも55.691度 の 部品が 60個 です。
六角形 五角形 の面をもつ部品は 必ず二つのクレィドルで作ってください。
そうでないとその部品は 全体を混乱させる 異物になってしまいます。
線対称ではなく 面対象です。
削った面の角度が 六角形用か 五角形用か 即座に判断がつかないことがあります。
加工後は 速やかに区別をができる しるしをを付けることを お勧めします。
私はホワイトボード用のマークペンを使っています 接着剤の影響を受けにくいようです。
今回の部品の大きさは 10×10の バルサ材で 4cm で作ろうとしています。
この多面体の稜の寸法を 1とし 六角形を底にした場合高さは 4.535cm になります。
ですから 完成品は 18cm ほどの大きさになります。
2012年6月12日
03[4,4,4] 16[5,6,6] 多面体 製作道具

レオナルドスタイルでの正六面体(Hexahedron) のつくり方を お伝えします。
画面の中にある クレィドルだけで加工ができます。
角材を 45度斜めに加工できる添え板にあわせ切断 整形するものです。
加工した角材の45度斜めの面を上にして 横側を同じく 45度斜めに整形します。
両端をこのように加工し 12個そろえれば部品は完成です。
この正六面体が きれいに正確に作れるようになると ちょっとした指物師気分です。
正六面体の正方形の中に 斜めに棒がついているのがありますが
その六面体の各面に 棒が斜めにあり 正四面体を形成しています。
さらに その斜めの棒に直角に棒を組み合わせると 前回お伝えした星型八面体になります。
そして 斜めの棒の稜にそって 正六面体を二分すると
この切断面は ダイヤモンド結晶模型製作図面として使った A4 の用紙と相似です (1:√2)。

次回は
サッカーボールでおなじみの 多面体の製作方法を お伝えしようかと思っています。
画面左には 以前作ったすす竹の多面体を載せたかったのですが
事故でばらばらになっていて修復を待っています。
右側は多面体ではなく
炭素結晶のフラーレン fullerene の模型として 作ったものです。
2012年6月9日
01[3,3,3] Compounds 多面体 製作道具

星型八面体について説明します。
稜の寸法が同じ二つの正四面体を
稜の中心を通って稜が直角に交差するように
合体させるとできる複合多面体 compounds です。
ヨハネス ケプラー(Johannes Kepler) が発見した(?)立体で
ステラ オクタンギュラ(Stella octangula)とよばれています。
部品の説明にはいります。
青く色のついた部品は 正四面体製作部品のマザー(mother) です。
その下の二つの 対になった部品が今回必要な部品で
ひとつの端を 35.3度 の面にカットし他端は直角になっています。
斜めになった面は正四面体と同じ作業ですが 直角になったところを
左右45度ずつ 90度に先端を切削する クレィドルで加工します。
赤く汚した部品のようにして 24個作ります。

部品の材料についてお話しします。
私の過去に製作した多面体の見本として 画面に載せているのは
ほとんど 5×5 のすす竹の “さい箸” で作っています。
寸法の 2/3 ほどは 5×5 の四角柱で 1/3 ほどが円錐状に削られています。
日曜大工の 材木売り場には売っていません。
初めは近くの観光地の土産売り場で買っていました。
20本入った袋が 500円から 1000円ほどしていました。
今は 一部の百円ショップで買えるようになりました。
レオナルドスタイル(Leonardo-style) に必要な材質のお勧めは
第一はなんと言ってもバルサ材です。
ただ 5×5 で作った作品で 鑑賞に値するものはなかなかできません。
材質がやわらかくて 直線の維持がむつかしく シィメトリーにするのに 技術力がいります。
腕をみがけば 5×5 のバルサ材でも すばらしい作品ができるはずです (私はまだですが)。
その次は プラ棒です 模型や フィギュアーの加工部品として売っています。
ドレサーでの加工で
速く切削操作をすると摩擦熱で切削面がやわらかくなり 加工が楽です。
ただ接着剤には 合成ゴム系のような性質がある透明タイプのものが必要です。
それと 断面が直角三角形の プラ棒もお勧めです。
クレィドルに使う溝の作成に重宝しています。
その次は ヒノキ材でしょう そして洋材が色々あり 最後がすす竹です。
そのせいもあり 私の作品はほとんど プロトタイプで 1点ものです。

今 手元にあるバルサ材のレオナルドスタイルは これらが全てです。
製作説明の作品として これから増えてゆくでしょう。
2012年6月8日
01[3,3,3] 多面体 製作道具
正四面体の作り方をお伝えします。
下の写真の A4用紙の図面をもとに製作します。
ダイヤモンド結晶模型で使った図面と基本は同じです。
長方向に用紙を二分し線をいれ 対角線を 2本いれます。
二分してできた小さな長方形に 対角線をいれます。

正四面体の左の稜の仰角と 赤い線で囲んだ三角形の左の辺
そして横のクレィドルの仰角 すべて同じ角度 54.7度です。
両端を 35.3度 (54.7度の余角) の面にカットした角棒を
このクレィドルで 面を垂直に置き 120度の接合面に切削します。
6個つくり 張り合わせれば完成です。
赤い線で囲んだ三角形の右下の角度 (70.5度) は 正四面体の面角になります。
四角形の角材で作る四面体の面角は 90度になり 少しふっくらとした形になります。
私はこのふくらみが気に入っています。
このような 面でない材料で作る多面体は
レオナルドスタイル(Leonardo-style) とよばれています。
商業用の URL ですが レオナルドスタイルの参考になるかもしれません。
http://rndmodelshop.com/geometrics
2012年6月7日
01[3,3,3] ダイヤモンド結晶

接合加工中です。
このように色々な形を作り それらを組み合わせてゆきます。

作業が少し進みました。
次回は ダイヤモンド結晶模型の基本図面から作る 正四面体や星型八面体。
そして 正六面体について お伝えしようかと思っています。

2012年6月5日
ダイヤモンド結晶 製作道具

10×10のバルサ材を 寸法50mm 角度 54.7度で のこぎりで切断し
ドレサーで整形しているところです。
切断のガイドは 10×10のバルサ材を二段にして 接着しています。
切断した残りの角材は 溝にそのままの状態で上に送り 同じ作業を繰り返します。
つまり 角度 54.7度の切断面は 点対象になっています。

左のクレィトドルは 70.5度の面を作るべく
のこぎりなどを使わず 直接 ドレサーで整形しています。
今回は 加工が容易なバルサ材を使っているためです。
右側は 70.5度の面を垂直に置き 120度の接合角に 整形しています。
作業は 繰り返し続けますが 部品の形状はこれで 完成です

左の作品は ダイヤモンド結晶模型製作の 見本として 撮影しようとして
誤って落としてしまい 修復する気がまだおこらず そのままにしています。
材質は すす竹で 部品寸法は 5×5の 20mmです。
右は 今回製作中のもので かなり ばかでかく写っています。

部品を 54.7×2 の 109.5度の角度に折れた溝に置き 木工用ボンドで接着しています。
前回説明しました図から この角度が得られます。
この形状がしっかり固まるまで そっとしておきます。
54.7×2 は 109.4 でなくて 109.5 なのは 精度を上げた数値 54.7は 54.74 だからです。
実際には そのような精度で 作図や加工はできていませんが
作業のもと資料には 可能なかぎり精度の高い値を意識してゆこうとしています。
2012年6月4日
01[3,3,3] ダイヤモンド結晶 製作道具

これが ダイヤモンド結晶模型(Crystalline Diamond Model) を作る 基本図面です。
正四面体とも関係が深いです。
A4 の用紙は 210×297 と寸法が規格で指定されており
縦横比が 1対 √2 に なっています そして 対角線が √3 です。
この用紙の 寸法比が とても大事です。
長方向に用紙を二分し線をいれ 対角線を 2本いれます。
二分してできた小さな長方形に 対角線をいれます。
右側の図は 一辺が 210mm の 正三角形をプロットし 三角形のかどから平行線をいれています。

左のクレィドルは 一定の寸法 (今回も 10×10 のバルサ材で 50mm でつくる予定です) と
一定形状 (この画像では 左 : 54.7度 右 : 70.5度) にするもので
スロゥプをつけず 板の接合線方向に 溝を接着します。
右は 一定寸法と 定形に整形されたパーツを 傾きをつけて (19.5度)
先端を 120度の角度で 整形するものです。

パーツの加工法のくわしくは 次回に お伝えします。
まずはサンプルと思い 作ってみました テトラポッド風の 作品です。
これを いくつも積み重ねてゆきます。
左の作品は 円柱でできています よりシィメトリックですが
四角柱での作品のほうが 私は好きです。
2012年6月1日
11[3,5,3,5] 多面体

やっと 二種類が完成しました。
左側の多面体が 今回作った Rhombic Triacontahedron 菱形30面体です。
製作プロセスを 画像に撮ろうとしたのですが
使用した接着剤の性質上 いっきに作業をすすめてしまいました。
木工用ボンドではなく 合成ゴム系の強力接着剤で
接着後 数十分は 接着剤に可塑性が残るためです。
いくら正確に加工しているつもりでも 接着のつど固化されてゆくと
全体が形づくられるときに 歪みが生じます。
この接着剤は 全パーツが接合されても まだ少し調整できるという 利点があります。
使用する量は ほんの少しですが 有機溶剤が含まれているため 注意が必要です。
次回は 多面体でばなく ダイヤモンド結晶模型について お伝えしようかなと思っています。
角度計算などはいらず A4の用紙 1枚ですみます
正四面体(Tetrahedron) とは兄弟関係ぐらいにあります。
少し準備作業や 諸事情がありますので しばらく時間をください 。
2012年5月29日
11[3,5,3,5] 多面体 製作道具

60個の部品を 製作しつつあるところです。
10.812度の傾斜で 120度の 接合面をもつ部分を製作するクレィドルと。
26.565度の傾斜で 72度の 接合面をもつ部分を製作するクレィドルで 作業しています。
緑色に汚してある部品は マザーです。
基準値から 少しでもマイナス方向に外れた 部品は捨ててしまいます。
安易に OKを出してしまった 部品を含んだ完成品は そのレベルの状態かそれ以下です。
ひとつひとつ 入魂をしながら つくってゆきます。
説明のための 今ここでの 10×10の寸法の角材での作品ではなく
5×5 ぐらいか それ以下の作品になると 良品選別には ルーペを用いて おこなっています。
(製作者の年齢からもたらす条件も 含まれています が)
2012年5月29日
<
1
2
3
4
5
6
7
8
9
10
11
12
13
>















































