RECENT POSTS
Excel 諸量
多面体[ 3,4,5,4 ] の Excel での諸量計算を リメイク版でお伝えしてきました。
パズル気分で求められると 言いましたので 実際に説明した方法で入力しました。
出てきた結果をまとめた数値が以下です。
| | 名称 | 基本数 | 稜芯寸 | 頂芯寸 |
| 01 | [3,3,3] | 0.577350269189626 | 0.353553390593274 | 0.612372435695795 |
| 02 | [3,3,3,3] | 0.707106781186548 | 0.5 | 0.707106781186548 |
| 03 | [4,4,4] | 0.816496580927726 | 0.707106781186547 | 0.866025403784438 |
| 04 | [3,3,3,3,3] | 0.85065080835204 | 0.809016994374948 | 0.951056516295154 |
| 05 | [3,4,3,4] | 0.866025403784439 | 0.866025403784441 | 1 |
| 06 | [3,6,6] | 0.904534033733291 | 1.06066017177982 | 1.17260393995586 |
| 07 | [3,3,3,3,4] | 0.928191377985572 | 1.24722316799365 | 1.34371337374461 |
| 08 | [3,4,4,4] | 0.933948831094465 | 1.30656296487638 | 1.39896632596591 |
| 09 | [5,5,5] | 0.934172358962716 | 1.30901699437495 | 1.40125853844408 |
| 10 | [4,6,6] | 0.948683298050514 | 1.5 | 1.58113883008419 |
| 11 | [3,5,3,5] | 0.951056516295154 | 1.53884176858764 | 1.6180339887499 |
| 12 | [3,8,8] | 0.959682982260667 | 1.70710678118654 | 1.77882364566392 |
| 13 | [3,3,3,3,5] | 0.972732850565596 | 2.0970538352521 | 2.15583737511565 |
| 14 | [3,4,5,4] | 0.97460776237817 | 2.17625089948281 | 2.23295050941568 |
| 15 | [4,6,8] | 0.976450976246513 | 2.2630334384537 | 2.31761091289276 |
| 16 | [5,6,6] | 0.979432085486414 | 2.42705098312482 | 2.47801865906759 |
| 17 | [3,10,10] | 0.985721919281302 | 2.92705098312486 | 2.96944901586341 |
| 18 | [4,6,10] | 0.991316689541059 | 3.76937712792159 | 3.80239449985117 |
| | [3,3,3,5] | 0.85065080835204 | 0.809016994374948 | 0.951056516295154 |
| | [4,4,5] | 0.862103722396976 | 0.850650808352042 | 0.986715155325985 |
2015年5月27日
14[3,4,5,4] Excel 諸量
今回も 多面体諸量をExcel で求める方法をお伝えした内容の リメイク版です。
[ 3,4,5,4 ] に限らず
プラトン多面体や アルキメデス多面体など
18 種類ある 値の計算ができます。以下三つの式です。
■( 2012年7月12日 斜方20・12面体[ 3,4,5,4 ] ) のリメイク版です。
角度をグラフ用紙に表示するための整数比換算の Excel 画面です。
色付けした全範囲を指定し 1 行目 A 列に copy and paste
| |
|
|
|
=SMALL(D2:D81,1) |
| 250 |
=TAN(RADIANS($G$2))*A2 |
=ROUND( TAN(RADIANS($G$2))*A2,0) |
=ABS(B2-C2) |
=IF(D2=$E$1,B2," ") |
仰角 |
12.9393184371119 |
| 249 |
=TAN(RADIANS($G$2))*A3 |
=ROUND( TAN(RADIANS($G$2))*A3,0) |
=ABS(B3-C3) |
=IF(D3=$E$1,B3," ") |
|
|
| |
B 列 から G 列 までの範囲を指定し セルの書式設定で
分類を 数値にし
小数点以下の桁数を 15 にしてください。
そして A 列 2 行目から E 列 3 行目までを範囲指定し
セルの右下にポインタを合わせ「+」を
81 行目までドラッグする [オートフィル]機能 を使います。
■( 2012年7月14日 斜方20・12面体[ 3,4,5,4 ] ) のリメイク版です。
頂芯寸 角数 から 面芯寸を求めます。
色付けした全範囲を指定し 1 行目 A 列に copy and paste
| |
頂芯寸 |
|
| |
2.23295050941567 |
|
| |
|
|
| 角数 |
多角形のかど心寸 |
面芯寸 |
| 3 |
=0.5/SIN(PI()/A5) |
=SQRT($B$2^2-B5^2) |
| 4 |
=0.5/SIN(PI()/A6) |
=SQRT($B$2^2-B6^2) |
| 5 |
=0.5/SIN(PI()/A7) |
=SQRT($B$2^2-B7^2) |
B 列 から C 列 までの範囲を指定し セルの書式設定で
分類を 数値にし
小数点以下の桁数を 15 にしてください。
■( 2012年8月18日
斜方20・12面体[ 3,4,5,4 ] ) のリメイク版です。
双対多面体の製作に必要な数値を求めます。
色付けした全範囲を指定し 1 行目 A 列に copy and paste
| |
稜芯寸 |
|
|
|
|
| |
2.176250899482800 |
|
|
|
|
| |
|
|
|
|
|
| 角数 |
多角形の辺心寸 |
面角 |
面芯寸 |
双対仰角 |
双対稜寸 |
| 3 |
=0.5/TAN(PI()/A5) |
=DEGREES(ACOS(B5/$B$2)) |
=SQRT($B$2^2-B5^2) |
=90-C5 |
=$B$2/D5*B5 |
| 4 |
=0.5/TAN(PI()/A6) |
=DEGREES(ACOS(B6/$B$2)) |
=SQRT($B$2^2-B6^2) |
=90-C6 |
=$B$2/D6*B6 |
| 5 |
=0.5/TAN(PI()/A7) |
=DEGREES(ACOS(B7/$B$2)) |
=SQRT($B$2^2-B7^2) |
=90-C7 |
=$B$2/D7*B7 |
| |
B 列 から F 列 までの範囲を指定し セルの書式設定で
分類を 数値にし
小数点以下の桁数を 15 にしてください。
2015年5月25日
14[3,4,5,4] Excel 諸量
2012年7月9日 に 多面体[ 3,4,5,4 ] の諸量計算を
Excel で説明していましたが 記述に誤りや 混乱がありました。
そこで Excel への入力を 容易にするよう
以下に 再度 計算式を 載せておきます。
正多面体 準正多面体 そして正多角柱 反角柱の 諸量が
パズル気分で 求められます。
最初は 12行目 B 列 に 9 を入れ
その下の B 列 の値を 全て 0 にします。
ある数を入れると 10行目のF列の表示が 360 以上 もしくは エラーになり
その数より 1つ上の値の数を入れると 360 以下になる場合
もとの数字にもどし 下の欄の数字の入力をします その繰り返しです。
27行目 c 列 に 求める値 基本数が表示されます。
求める 多面体の 多角形の種類が 1 や 2 しかない場合
二番目や三番目の 入力欄には 個数 1 角数 2 としても OK です。
二角形 (角度は 0 ) のダミーです。
色付けした全範囲を指定し 1 行目 A 列に copy and paste
| 個数 |
角数 |
頂角度(R) |
頂角度(D) |
側角度(R) |
側角度(D) |
角底寸/2 |
| 1 |
3 |
=(PI()/2-PI()/B2)*2 |
=DEGREES(C2) |
=PI()/B2 |
=DEGREES(E2) |
=COS(E2) |
| 2 |
4 |
=(PI()/2-PI()/B3)*2 |
=DEGREES(C3) |
=PI()/B3 |
=DEGREES(E3) |
=COS(E3) |
| 1 |
5 |
=(PI()/2-PI()/B4)*2 |
=DEGREES(C4) |
=PI()/B4 |
=DEGREES(E4) |
=COS(E4) |
| |
|
|
|
|
|
|
| |
|
底面 側角度(R) |
底面 頂角度(R) |
底面 頂角度(D) |
底面 総頂角度(D) |
接合角 |
| |
=B2 |
=ACOS(G2/$C$27) |
=(PI()/2-C7)*2 |
=DEGREES(D7) |
=E7*A2 |
=E7/2 |
| |
=B3 |
=ACOS(G3/$C$27) |
=(PI()/2-C8)*2 |
=DEGREES(D8) |
=E8*A3 |
=E8/2 |
| |
=B4 |
=ACOS(G4/$C$27) |
=(PI()/2-C9)*2 |
=DEGREES(D9) |
=E9*A4 |
=E9/2 |
| |
|
|
|
|
=SUM(F7:F9) |
|
| |
|
|
|
|
|
|
| 1 |
9 |
=B12*1/10^A12 |
|
|
|
|
| 2 |
7 |
=B13*1/10^A13 |
|
仰角 |
|
|
| 3 |
4 |
=B14*1/10^A14 |
|
=DEGREES(ACOS(C27)) |
|
|
| 4 |
6 |
=B15*1/10^A15 |
|
|
|
|
| 5 |
0 |
=B16*1/10^A16 |
|
|
|
|
| 6 |
7 |
=B17*1/10^A17 |
|
稜芯寸 |
|
|
| 7 |
7 |
=B18*1/10^A18 |
|
=0.5*C27/SQRT(1-C27^2) |
|
|
| 8 |
6 |
=B19*1/10^A19 |
|
|
|
|
| 9 |
2 |
=B20*1/10^A20 |
|
|
|
|
| 10 |
3 |
=B21*1/10^A21 |
|
頂芯寸 |
|
|
| 11 |
7 |
=B22*1/10^A22 |
|
=0.5/SQRT(1-C27^2) |
|
|
| 12 |
8 |
=B23*1/10^A23 |
|
|
|
|
| 13 |
1 |
=B24*1/10^A24 |
|
|
|
|
| 14 |
7 |
=B25*1/10^A25 |
|
|
|
|
| 15 |
0 |
=B26*1/10^A26 |
|
|
|
|
| |
|
=SUM(C12:C26) |
|
|
|
|
C 列 から G 列 までの範囲を指定し セルの書式設定で
分類を 数値にし
小数点以下の桁数を 15 にしてください。
2015年5月24日
18[4,6,10] sphericity
Wikipedia は 色々な言語でも 調べものができる 大変便利なツールです。
多面体 [4,6,10] を Wikipedia の なにか一つの言語で調べると 以下の言語でも
検索できるよう リンクがされています。
ca Icosidodecàedre truncat カタロニア語
de Großes Rhombenikosidodekaeder ドイツ語
el Κόλουρο εικοσιδωδεκάεδρο ギリシャ語 **
en Truncated icosidodecahedron 英語
eo Senpintigita dudek-dekduedro エスペラント語
es Icosidodecaedro truncado スペイン語
eu Ikosidodekaedro moztu バスク語
fr Icosidodécaèdre tronqué フランス語
it Icosidodecaedro troncato イタリア語
ja 斜方切頂二十・十二面体 日本語
ko 깎은 십이이십면체 韓国語
nl Afgeknotte icosidodecaëder オランダ語
no Avstumpet ikosidodekaeder ノルウェー語
pt Icosidodecaedro truncado ポルトガル語
th ทรงสามสิบสองหน้าปลายตัด タイ語
zh 大斜方截半二十面体 中国語
計算式や 数値にはまだ いくつかの言語では 混乱がみられます。 (2015年5月15日 現在)
ロシア語への リンクが追加されています。 (2015年8月27日 確認)
ru Ромбоусечённый икосододекаэдр
スロベニア語への リンクが追加されています。 (2017年1月14日 確認)
sl Prisekani ikozidodekaeder
ポーランド語への リンクが追加されています。 (2017年7月31日 確認)
pl Dwudziesto-dwunastościan rombowy wielki
** ギリシャ語版が 英語版と同じ 計算式 数値に変更されました。(2017年 8月 5日)
2015年5月15日
BASIC 未分類
久しぶりです。
多面体関連の内容で 今はお伝えするほどのエピソードはありません。
そこで やっと出来た BASIC プログラムを載せておきます。
以前 Excel で作ったこともある 簡単なロジックで作っています。
仮定を設けての推論はせず 論理的必然としての 結果を表示します。
Excel では IF文が錯綜し 頭が混乱しました。
! 数独 初級 攻略 ツール
! フリーウエアー 十進BASIC でプログラム
! http://hp.vector.co.jp/authors/VA008683/ を参照
! http://hp.vector.co.jp/authors/VA008683/english/index.htm 英語版
OPTION BASE 0
DIM x001(9,10) ! 集計用配列
DIM s001(9,9) ! 問題データ格納
DIM s002(9,9) ! 判定用数値格納
DIM s003(9,9) ! 累積判定用数値格納
! 集計振り分け用データ取り込み
FOR x=1 TO 9
FOR y=1 TO 9
READ x001(x,y)
NEXT y
NEXT x
! 集計振り分け用データ
DATA 1,1,1, 2,2,2, 3,3,3
DATA 1,1,1, 2,2,2, 3,3,3
DATA 1,1,1, 2,2,2, 3,3,3
DATA 4,4,4, 5,5,5, 6,6,6
DATA 4,4,4, 5,5,5, 6,6,6
DATA 4,4,4, 5,5,5, 6,6,6
DATA 7,7,7, 8,8,8, 9,9,9
DATA 7,7,7, 8,8,8, 9,9,9
DATA 7,7,7, 8,8,8, 9,9,9
! 問題データ取り込み と 集計データ格納
FOR x=1 TO 9
FOR y=1 TO 9
READ w001
IF w001 = 0 THEN LET s002(x,y)=0
IF w001 > 0 THEN LET s002(x,y)=10^(w001-1)
LET s001(x,y)=w001
LET x001(x,0)=x001(x,0)+s002(x,y)
LET x001(0,y)=x001(0,y)+s002(x,y)
LET w002=x001(x,y)
LET x001(w002,10)=x001(w002,10)+s002(x,y)
NEXT y
NEXT x
PRINT ! 1行スぺースを空ける
! 問題内容を 視覚化
FOR x=1 TO 9
FOR y=1 TO 9
IF s001(x,y)=0 THEN
PRINT "□ ";
ELSE
PRINT s001(x,y);
END if
IF y=3 OR y=6 THEN PRINT " ";
IF y=9 THEN PRINT
NEXT y
IF x=3 OR x=6 THEN PRINT
NEXT x
! 個々の位置に判定数値を格納
FOR x=1 TO 9
FOR y=1 TO 9
LET w001=x001(x,y)
IF s002(x,y) = 0 THEN
LET s003(x,y)=x001(x,0)+x001(0,y)+x001(w001,10)
END if
NEXT y
NEXT x
PRINT ! 1行スぺースを空ける
! 個々の判定数値を表示
FOR x=1 TO 9
FOR y=1 TO 9
IF s003(x,y) = 0 THEN
PRINT "[ ";s001(x,y);" ]";" ";
ELSE
LET w006$=""
LET w004$= STR$(s003(x,y)+10^9)
FOR z=1 TO 9
LET zz=10-z
LET w005$=mid$(w004$,z+1,1)
IF w005$="0" THEN
LET w006$=w006$ & STR$(zz)
ELSE
LET w006$=w006$ & " "
END if
NEXT z
PRINT w006$;" ";
END IF
IF y=3 OR y=6 THEN PRINT " ";
IF y=9 THEN PRINT
NEXT y
IF x=3 OR x=6 THEN PRINT
NEXT x
! 問題データ
! a b c d e f g h i
DATA 0,0,0, 0,0,7, 0,8,0 ! 1
DATA 0,0,0, 0,0,0, 0,2,3 ! 2
DATA 1,6,4, 0,0,0, 0,0,0 ! 3
DATA 2,0,7, 1,8,6, 0,0,0 ! 4
DATA 0,8,1, 9,5,0, 0,7,0 ! 5
DATA 9,4,5, 0,0,3, 0,0,6 ! 6
DATA 4,1,2, 0,6,0, 7,0,8 ! 7
DATA 0,0,6, 4,0,9, 2,3,1 ! 8
DATA 3,7,9, 2,0,8, 4,0,5 ! 9
END
以上です。下のような出力になります。
□ □ □ □ □ 7 □ 8 □
□ □ □ □ □ □ □ 2 3
1 6 4 □ □ □ □ □ □
2 □ 7 1 8 6 □ □ □
□ 8 1 9 5 □ □ 7 □
9 4 5 □ □ 3 □ □ 6
4 1 2 □ 6 □ 7 □ 8
□ □ 6 4 □ 9 2 3 1
3 7 9 2 □ 8 4 □ 5
5 9 5 32 3 65 3 9 4321 [ 7 ] 9 65 1 [ 8 ] 9 4
87 5 9 5 8 8 65 9 4 1 54 1 9 65 1 [ 2 ] [ 3 ]
[ 1 ] [ 6 ] [ 4 ] 8 5 3 9 32 5 2 9 5 9 5 9 7
[ 2 ] 3 [ 7 ] [ 1 ] [ 8 ] [ 6 ] 9 5 3 9 54 9 4
6 [ 8 ] [ 1 ] [ 9 ] [ 5 ] 4 2 3 [ 7 ] 4 2
[ 9 ] [ 4 ] [ 5 ] 7 7 2 [ 3 ] 8 1 1 [ 6 ]
[ 4 ] [ 1 ] [ 2 ] 5 3 [ 6 ] 5 [ 7 ] 9 [ 8 ]
8 5 5 [ 6 ] [ 4 ] 7 [ 9 ] [ 2 ] [ 3 ] [ 1 ]
[ 3 ] [ 7 ] [ 9 ] [ 2 ] 1 [ 8 ] [ 4 ] 6 [ 5 ]
2015年4月19日
多面体
以下の画像が 今現在 手元にある
すす竹風の材で作った多面体の ほぼすべてです。
バルサ材で作った もっと大きな多面体は ほとんどありません。
フリーマーケットで 手放しています。
後で気がついたのですが
プロトタイプの一点ものもありました。
また作ればいいのです。別の材で。

今年最初のブログで …
今年は “初心” という言葉を意識した表現をめざします。
と書きました。
“初心” とは いい言葉です。
“初心を忘れるな” と
世阿弥(1363年? – 1443年? )が花鏡で 伝えています。
未完であることを自覚し向上しようとする人が 初心者 だと言えます。
似た言葉の初級者 は 未完であることは同じですが
向上心があるかはわかりません。
私も 初心者として つれづれとブログを 書き綴ってゆこうと思っています。
追伸
以前 多面体諸量を得るための計算式を Excel でものせていましたが
今の私のパソコンにはいっている Excel では うまく動作しないのがありました。
そこで Excel 2010 で動作するように 式を変更したり
作成説明の表現を 改善したのもあります。
2015年3月25日
ダイヤモンド結晶 嵯峨近辺
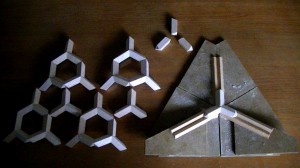
情景小物の消波ブロックを使って ダイヤモンド結晶模型を作ってみます。
画像 左上は 小さく結晶構造を表現しています。
方向を合わせて部品を組み上げているだけなので作業は簡単です。
しかし 部品の中芯も炭素原子であり そして
それそれれの突起が四本集まる空洞部分も炭素原子となって
シンメトリーさを犠牲にしてしまいます。
そこで 炭素原子と炭素原子とを結ぶ突起部分を
長さの半分がそれぞれの炭素原子に付いているものと考えます。
部品と部品の結合は
三本ずつある接着していない突起の向きを
二つの突起を接合した方向を軸として 60度ずらします。
つまり 軸方向に見ると 手前の 120度開いた突起の間に相手の突起がきます。
今回 お見せしている作り方は
6つの部品を ジグザグしながら 環になっているユニット 1つと
1つの部品に 3方向から 60度 向きを変えて接合した ユニットを
複数個作る方法です。
画面上部にある 環状のユニットに 三又状のユニットを結合すれば
前回説明しました 単位格子の中の構造と同じになります。
それに 次々と 三又状ユニットを結合してゆくと 構造が
大きくなってゆきます。
三又状ユニットだけでは 収まらなくなる場合も出てきますが
接合ルールに従って 部品を埋めてゆきます。

追伸
今日 近くのお寺(清涼寺)で お松明式という行事があります。
京都三大火祭の一つだそうです。他は「大文字五山送り火」「鞍馬の火祭」です。
以下の画像が その準備中の情景です。10m 程の高さの松明が 3本立てられます。
20:30頃 それらに火がつけられ夜空を焦がします。
見るのが待ち遠しいです。 2015 3月15日 11:05

2015年3月15日
ダイヤモンド結晶
前回 ダイヤモンド結晶模型の製作方法の説明を
言葉足らずのまま 終わってしまいました。説明を すこし進めます。
下の画像の 透明な正六面体の中に入っている 左側の立体が
ダイヤモンドの単位格子として 一般に表現されている図を
実際に確認できる物として 具体化したものです。(拡大は左クリック)
参考にした図は 結晶学の 論理的帰結として よく目にするものですが
立体的にイメージするのが困難でした。
右側の透明な正六面体の中に入っている 立体を 四つくっつけると
同じ形状になります。
つまり 透明な正六面体を 手前二列 奥二列 で四つ並べ 1段目とし
同じように 2段目を上に載せます。
右側の立体と同じ形 同じ向きの状態で 下一段目は 手前右 奥左
上二段目は 手前左 奥右と 設置します。
画像下左にある 白いのは消しゴムでできた 消波ブロックの模型です。
その横のは 鉄道模型の情景小物として 売られているものです。
この小物を用いて 画像下の立体を作っています。
接着剤は 合成ゴム系ボンドで 簡単につくれました。
この場合 部品の突起部分は 炭素原子と
他の炭素原子との中間位置までの電子雲として表現しています。

追伸
この 記事の投稿をして すぐに 中国 エジプト ロシア などの国から アクセスがはいりました。
現在も アクセス人数は 日本からと 海外からとの比は 大体 1 対 1 です。
どんなテーマに 関心が持たれているのか 判りませんが
今後も思いつくまま 不定期に 記述していこうと思っています。
2015年3月11日
ダイヤモンド結晶
久しぶりの投稿です。
丸棒で作る ダイヤモンド結晶模型の製作方法についてです。
ブログ内検索の “ダイヤモンド結晶” のカテゴリーをクリックすると
この記事とあわせて 今までの説明も見られます。
下画像 右上の模型は 長さ 20mm 直径 10mm のバルサ材の丸棒で作りました。
(画像をクリックすると 拡大画像になるはずです。)
その左側にある 八つの部品でできた
ジグザグ状のユニットのみの構成でできています。
以前は角棒での製作についてでしたので 加工部分の回転ズレを考慮する必要はありませんでした。
今回は 円柱の断面部分の二か所の加工になります。
両面それぞれの加工形状が正確であるだけでなく 形状の位置関係も重要です。
その作業の補助として 鉛筆の断面のような治具を作りました。
一つの 丸棒部品の周りに 六つの部品が取り囲む状態になっています。
この治具をもとに 一定寸法に加工した円柱に 円に接する正三角形を鉛筆で書きます。
一つの面が書き終わったら この挿入状態を維持しながら
反対側の面にも 同じように正三角形を描きます。
ただし 三角形の かど位置 は一つの部品分をずらしてです。
この三角形のそれぞれの 辺 を基準として 切削をしますが円柱面の中の正三角形は 平面のままに残します。
この加工でできた 四つの部品でできた テトラボッド状のユニットの 中芯は 正四面体の空洞となります。

ことば足らずですが 表現を考えていると いつまでたっても投稿できそうにないので 終えておきます。
2015年3月3日
18[4,6,10] sphericity 多面体 諸量
以前 英語版の Wikipedia での表面積計算が 多面体[4,6,10]
Truncated icosidodecahedron (=Rhombitruncated Icosidodecahedron)
では私の計算と異なると書きましたが
今日 (2015年1月8日) 確認したところ
英語版の Wikipedia で 計算式が変更され 答えが 174.2920303 (稜寸=1として)
になっていました。
私の計算結果と同じになったことに 嬉しく思っています。
2015年1月8日
嵯峨近辺 未分類
明けまして おめでとうございます。
今年も 多面体などに関連したことを 思いつくまま
ブログに載せてゆこうと思っています。
どうぞ よろしくお願いします。
昨年は サイバー攻撃などの不本意なアクセスを避けるため
双方向の通信機能を犠牲にしていましたが
それでも 私の製作方法の説明記述は 初心者向きではない
という 数人の方の意見をお伺いすることができました。
今年は “初心” という言葉を意識した表現をめざします。
例年になく 雪が積もっています。
昨夜は 天候が悪く 除夜の鐘をつきにゆく気になれませんでした。
そこのお寺でいただける おぜんざいが 目当ての半分だったのですが。
そのかわり今日 近くの神社でお神酒をいただいてきました。
いつもだと 二日目では 樽の底に少し残っている程度ですが
今回は ぐい飲みほどの酒を 飲んでしまいました。
2015年1月2日
嵯峨近辺 未分類
今日 京都嵯峨芸術大学のフリーマーケットにいって 多面体を売ってきました。
女ものの商品が多く 訪れる方たちも女性が多くおられました。
多面体に興味を示される方が少ないようで
“何に使うもんなんやろう” と言って通り過ぎる人もおられました。
でも それからしばらくして “これが 噂の多面体や わあすごい” とか
“思ってたより ずっとええやん”
とかという言葉を発する方たちが来られるようになり
自慢げに説明する自分がいました。
一般の人ではなく 応募の時に添付した多面体の写真を
すでに見ていた 運営委員の中の人たちでした。
3Dプリンターて作った 作品を持ってきて説明してくださり
名刺までいただいた教授もおられました。
この後は 一般の方も含めて 身に余る
お褒めのお言葉をいただく波が 数回おとずれました。
小は 500円 大は 1000円~ と表示をしていましたが
そのつど ゼロ円を含めて 気前のいい値段付けをしました。
そして ほとんどの品を持って帰ってもらいました。
気づけば 下の写真 一枚しか撮っていませんでした。まだ準備中です。

2014年10月11日
未分類
以前 作品が溜まってしまったと お伝えしました。(2014年7月21日)
製作の説明のために 10mm ×10mm の角材でつくったものですが
かさばっています。
家が大きいとはとてもいえず 生活空間に問題が発生しそうな状態です。
たまたま フリーマーケットへの出店案内のチラシが 届いていました。
バラして 再利用するより 人のなにかの用に供することができればと思いました。
そこで 一度は経験するのもいいかと 応募してみました。
下の画像は 作品に名前のラベルを付けているところです。
ラベルの下のスペースに 単価を記入しておくべきですが まだ空白のままです。
“二束三文” という言葉が頭にうかんできます。
多面体に 関心があったり 興味を示してくださる方がおられれば
ただでお譲りしてもいいのですか と主催者側に問い合わせると OK でした。
でも その判断をする基準は?
“美術的創作物” として目指しているのではなく
“由緒ある多面体” の模型として 目に見える 正確な形を求めて作ったものです。
私の経験では 身内や知人にはそのように感じてくれる人は まれでした。

追伸
10月11日 京都嵯峨芸術大学での フリマです。
2014年10月8日
BASIC 多面体 諸量
今回は 双対多面体の体積や 面積計算の BASIC プログラムを載せておきます。
双対多面体の場合 何を基準として 体積や面積を表現すべきか悩むところです。
以下にその出力の値を表示します。
体積1 や 面積1 は すでにお伝えしている値なので省略し 名称を追加しておきます。
体積2 や 面積2 は 双対多面体の稜の寸法の一番小さい値を 1 としたときの値です。
有効桁数は 13 ぐらいです。
双対体積2 双対面積2
.11785113019776 1.73205080756889 01 双対[3,3,3] Tetrahedron
1.00000000000001 6.00000000000001 02 双対[3,3,3,3] Hexahedron
.471404520791039 3.46410161513776 03 双対[4,4,4] Octahedron
7.66311896062464 20.6457288070676 04 双対[3,3,3,3,3] Dodecahedron
3.07920143567805 11.3137084989848 05 双対[3,4,3,4] Rhombic Dodecahedron
.982092751648015 5.52770798392574 06 双対[3,6,6] Triakis Tetrahedron
35.6302020120718 54.7965494386598 07 双対[3,3,3,3,4] Pentagonal Icositetrahedron
14.9133887137866 30.6948957240312 08 双対[3,4,4,4] Trapezoidal Icositetrahedron
2.18169499062494 8.66025403784447 09 双対[5,5,5] Icosahedron
3.5555555555556 11.9256958799988 10 双対[4,6,6] Tetrakis Hexahedron
12.3107341487011 26.8328157299974 11 双対[3,5,3,5] Rhombic Triacontahedron
2.91421356237319 10.6729418739837 12 双対[3,8,8] Triakis Octahedron
189.78985206689 162.698964198467 13 双対[3,3,3,3,5] Pentagonal Hexecontahedron
81.0041436353778 92.2319129064044 14 双対[3,4,5,4] Trapezoidal Hexecontahedron
16.288919082924 32.0667340105321 15 双対[4,6,8] Hexakis Octahedron
13.4585693663192 27.9352496007011 16 双対[5,6,6] Pentakis Dodecahedron
12.0172209268751 26.2285959767441 17 双対[3,10.10] Triakis Icosahedron
84.181975440052 94.2346326621943 18 双対[4,6,10] Hexakis Icosahedron
以下がプログラムです。
今回も2013年1月11日に掲載した 計算プログラムで算出した諸量をもとに
表面積計算を追加して求めています。
OPTION ANGLE DEGREES
DIM d01(18,8) ! 双対多面体の諸量
DIM d02(10,03) ! 正多角形の諸量
DIM d03$(18,2) ! 最小寸法の稜の形態と名称
FOR d04=1 TO 18
FOR d05 =1 TO 8
READ d01(d04,d05) ! 双対多面体の諸量の読み込み
NEXT d05
READ d03$(d04,1) ! 最小寸法の稜の形態の読み込み
READ d03$(d04,2) ! 名称の読み込み
NEXT d04
FOR d06 = 1 TO 6 ! 正多角形の諸量計算
READ d07
LET d02(d07,1) = 0.5/SIN(180/d07) !正多角形の かど心寸
LET d02(d07,2) = 0.5/TAN(180/d07) !正多角形の 辺心寸
LET d02(d07,3) = SIN((180-360/d07)/2) !正多形の内角を二等辺三角形の頂角
! !としたときの 底辺の1/2の長さ
NEXT d06
PRINT " 双対体積1"," 双対面積1", " 双対体積2"," 双対面積2"
FOR d08=1 TO 18
LET d09=d01(d08,1)
LET d10=d01(d08,2)
LET d11=d01(d08,3)
LET d12=d01(d08,4)
LET d13=d01(d08,5)
LET d14=d01(d08,6)
LET d15=d01(d08,7)
LET d16 = d01(d08,8) ! 基本数 頂芯寸が 1 のときの 稜芯寸
LET d17 = d16/(SQR(1-d16^2)*2) ! 稜芯寸
LET d18 = SQR((1/SQR(1-d16^2)/2)^2 - d02(d09,1)^2) ! L面芯寸
LET d19 = SQR((1/SQR(1-d16^2)/2)^2 - d02(d10,1)^2) ! M面芯寸
LET d20 = SQR((1/SQR(1-d16^2)/2)^2 - d02(d11,1)^2) ! S面芯寸
LET d21 = d02(d09,2) * d17 / d18 ! 双L稜寸(=L辺心寸*稜芯寸/L面芯寸)
LET d22 = d02(d10,2) * d17 / d19 ! 双M稜寸(=M辺心寸*稜芯寸/M面芯寸)
LET d23 = d02(d11,2) * d17 / d20 ! 双S稜寸(=S辺心寸*稜芯寸/S面芯寸)
LET d24=d02(d09,3)
LET d25=d02(d10,3)
LET d26=d02(d11,3)
LET d27 = SQR(d21^2 - (d24/2)^2) + SQR(d16^2 - d24^2)/2 ! 双Lかど心寸
LET d28 = SQR(d22^2 - (d25/2)^2) + SQR(d16^2 - d25^2)/2 ! 双Mかど心寸
LET d29 = SQR(d23^2 - (d26/2)^2) + SQR(d16^2 - d26^2)/2 ! 双Sかど心寸
LET d30 = d27 * d02(d09,3)/2 * d12 !
LET d31 = d28 * d02(d10,3)/2 * d13 !
LET d32 = d29 * d02(d11,3)/2 * d14 !
LET d33 = (d30+d31+d32) * d15 ! 面積
LET d34 = 1/SQR(1-d16^2)/2-SQR(1-d16^2)/2 ! 双面芯寸
LET d35=d33*d34/3 ! 体積
LET d36=SQR(1-d16^2)
LET d37=1/(d36*2)-d36/2
PRINT d35,d33, ! 元の多面体の稜寸が 1 のときの 稜芯寸と同じ値の体積と面積
IF d03$(d08,1)="LL" THEN LET d38 = d21+d21
IF d03$(d08,1)="LM" THEN LET d38 = d21+d22
IF d03$(d08,1)="MM" THEN LET d38 = d22+d22
IF d03$(d08,1)="MS" THEN LET d38 = d22+d23
PRINT d35/d38^3, ! 双対多面体の一番寸法が小さい稜寸を 1 としたときの体積
PRINT d33/d38^2, ! 双対多面体の一番寸法が小さい稜寸を 1 としたときの面積
PRINT d03$(d08,2)! 名称
NEXT d08
! <<計算に必要な既に分かっている定数 (角数の2は 角度0)>>
! |← 1つの頂の諸量 →|
! 01 02 03 04 05 06 07 08 09 10
! M角数 L個数 S個数
! L角数 S角数 M個数 頂数 基本数 最小稜形
DATA 3, 2, 2, 3, 1, 1, 4, .577350269189627 , "LL", "01 双対[3,3,3]"
DATA 3, 2, 2, 4, 1, 1, 6, .707106781186549 , "LL", "02 双対[3,3,3,3]"
DATA 4, 2, 2, 3, 1, 1, 8, .816496580927728 , "LL", "03 双対[4,4,4]"
DATA 3, 2, 2, 5, 1, 1, 12, .850650808352041 , "LL", "04 双対[3,3,3,3,3]"
DATA 4, 3, 2, 2, 2, 1, 12, .86602540378444 , "LM", "05 双対[3,4,3,4]"
DATA 6, 3, 2, 2, 1, 1, 12, .904534033733292 , "LM", "06 双対[3,6,6]"
DATA 4, 3, 2, 1, 4, 1, 24, .928191377985573 , "MM", "07 双対[3,3,3,3,4]"
DATA 4, 3, 2, 3, 1, 1, 24, .933948831094466 , "LM", "08 双対[3,4,4,4]"
DATA 5, 2, 2, 3, 1, 1, 20, .934172358962716 , "LL", "09 双対[5,5,5]"
DATA 6, 4, 2, 2, 1, 1, 24, .948683298050515 , "LM", "10 双対[4,6,6]"
DATA 5, 3, 2, 2, 2, 1, 30, .951056516295154 , "LM", "11 双対[3,5,3,5]"
DATA 8, 3, 2, 2, 1, 1, 24, .959682982260668 , "LM", "12 双対[3,8,8]"
DATA 5, 3, 2, 1, 4, 1, 60, .972732850565597 , "MM", "13 双対[3,3,3,3,5]"
DATA 5, 4, 3, 1, 2, 1, 60, .974607762378171 , "MS", "14 双対[3,4,5,4]"
DATA 8, 6, 4, 1, 1, 1, 48, .976450976246514 , "MS", "15 双対[4,6,8]"
DATA 6, 5, 2, 2, 1, 1, 60, .979432085486415 , "LM", "16 双対[5,6,6]"
DATA 10, 3, 2, 2, 1, 1, 60, .985721919281303 , "LM", "17 双対[3,10.10]"
DATA 10, 6, 4, 1, 1, 1,120, .99131668954106 , "MS", "18 双対[4,6,10]"
DATA 3, 4, 5, 6, 8, 10
END
2014年8月30日
18[4,6,10] BASIC Excel sphericity 多面体 諸量
前回 英語版の Wikipedia での表面積計算が 多面体[4,6,10]
Truncated icosidodecahedron (=Rhombitruncated Icosidodecahedron)
では私の計算と異なると書きましたが *注
英語版や他の多くの言語の Wikipediaに載せられた 計算式を
BASICで実行すると以下です。(稜寸=1として)
LET a=30*(1+SQR(2*(4+SQR(5)+SQR(15+6*SQR(6)))))
PRINT a
END
答=175.031044595664
ドイツ語版(Großes Rhombenikosidodekaeder)
の式です。(稜寸=1として)
LET b=30*(1+SQR(3)+SQR(5+2*SQR(5)))
PRINT b
END
答=174.292030342324
イタリア語版(Icosidodecaedro troncato)は (稜寸=1として)
LET x=30*(1+SQR(2*(4+SQR(5)+SQR(15+6*SQR(5)))))
PRINT x
END
答=174.292030342324
式の最後の 6*SQR(5) が 英語版の 6*SQR(6) と異なっています。
オランダ語版(Afgeknotte icosidodecaëder)や
ポルトガル語版(Icosidodecaedro truncado スペイン語と同じスペル)では
式は英語版と同じなのに
答えの記述は 174,2920 になっています。
少しためらいもありましたが くどくどと書いてしまいました。
*英語版は 計算式、数値とも変更されています。(2015年1月8日現在)
上記 三種類の計算式を Excel で表示すると以下です。
=30*(1+SQRT(2*(4+SQRT(5)+SQRT(15+6*SQRT(6)))))
=30*(1+SQRT(3)+SQRT(5+2*SQRT(5)))
=30*(1+SQRT(2*(4+SQRT(5)+SQRT(15+6*SQRT(5)))))
2014年7月25日
18[4,6,10] BASIC sphericity 多面体 諸量
2013年8月11日に多面体の球形度をお伝えしていますが
数値だけで 計算根拠を載せていませんでした。
別々に作ったプログラムでの計算数値を比較して 正確性をチェックしていました。
その時点では 公表されている 資料が手元になく少し不安が残っていました。
先日 英語版の Wikipedia での表面積計算が Truncated icosidodecahedron
斜方切頂20・12面体 [4,6,10] で 175.031045 となっているのを発見しました。 *注
私の計算結果は174.29203034232392088 です。
また やってしまったかと思い 他の言語の Wikipedia も調べると、
ドイツ語版の数式を計算すると 私と同じ結果になりました。すこし安心しました。
不安を一掃するために もう一度計算プログラムを作ってみました。
2013年1月11日に掲載した 計算プログラムで算出した諸量をもとに
表面積計算を追加して求めています。判断を仰ぎます。
OPTION ANGLE DEGREES
OPTION BASE 0
DIM x001(10) ! 多角形の面積
DIM x002(18,6) ! 既知諸量
DIM x003$(18) ! 名称
DIM x004(18,4) ! 頂芯寸 面芯寸
FOR x=1 TO 6
READ m
LET x001(m)=0.5/TAN(180/m)*m*0.5 ! 多角形面積入力
NEXT x
FOR y=1 TO 18
FOR z=1 TO 6
READ x002(y,z) ! 数値入力
NEXT z
READ x003$(y) ! 名称入力
NEXT y
FOR p=1 TO 18
FOR q=1 TO 4
READ x004(p,q)
NEXT q
NEXT p
PRINT "名称",
PRINT " 外接球半径 = R",
PRINT " 表面積 = S ",
PRINT " 体積 = V ",
PRINT " V/(S*R)"
FOR u=1 TO 18
LET f11=x002(u,1)
LET f12=x002(u,2)
LET f13=x002(u,3)
LET f21=x002(u,4)
LET f22=x002(u,5)
LET f23=x002(u,6)
LET g10=x004(u,1)
LET g11=x004(u,2)
LET g12=x004(u,3)
LET g13=x004(u,4)
LET h01=x001(f11)*f21
LET h02=x001(f12)*f22
LET h03=x001(f13)*f23
LET i01=h01*g11
LET i02=h02*g12
LET i03=h03*g13
PRINT x003$(u),
PRINT g10,
PRINT h01+h02+h03,
PRINT (i01+i02+i03)/3,
PRINT (i01+i02+i03)/3 / ( g10 * (h01+h02+h03) )
NEXT u
DATA 3,4,5,6,8,10 ! 多角形の種類
! 角数 総数
DATA 3, 0, 0, 4, 0, 0, "01[3,3,3]"
DATA 3, 6, 0, 4, 4, 0, "06[3,6,6]"
DATA 3, 0, 0, 8, 0, 0, "02[3,3,3,3]"
DATA 4, 0, 0, 6, 0, 0, "03[4,4,4]"
DATA 3, 8, 0, 8, 6, 0, "12[3,8,8]"
DATA 3, 4, 0, 8, 6, 0, "05[3,4,3,4]"
DATA 3, 0, 0, 20, 0, 0, "04[3,3,3,3,3]"
DATA 5, 0, 0, 12, 0, 0, "09[5,5,5]"
DATA 4, 6, 0, 6, 8, 0, "10[4,6,6]"
DATA 3,10, 0, 20,12, 0, "17[3,10.10]"
DATA 3, 4, 0, 8,18, 0, "08[3,4,4,4]"
DATA 3, 5, 0, 20,12, 0, "11[3,5,3,5]"
DATA 4, 6, 8, 12, 8, 6, "15[4,6,8]"
DATA 3, 4, 0, 32, 6, 0, "07[3,3,3,3,4]"
DATA 5, 6, 0, 12,20, 0, "16[5,6,6]"
DATA 4, 6,10, 30,20,12, "18[4,6,10]"
DATA 3, 4, 5, 20,30,12, "14[3,4,5,4]"
DATA 3, 5, 0, 80,12, 0, "13[3,3,3,3,5]"
! 頂芯寸 S面芯寸 M面芯寸 L面芯寸
DATA .612372435695795, .204124145231932, 0 , 0 ! 01
DATA 1.17260393995586, 1.02062072615966, .6123724356958 , 0 ! 06
DATA .707106781186549, .408248290463865, 0 , 0 ! 02
DATA .866025403784443, .500000000000007, 0 , 0 ! 03
DATA 1.77882364566394, 1.68252198471218, 1.20710678118657, 0 ! 12
DATA 1 , .816496580927726, .707106781186547, 0 ! 05
DATA .951056516295157, .755761314076175, 0 , 0 ! 04
DATA 1.40125853844408, 1.11351636441161, 0 , 0 ! 09
DATA 1.58113883008421, 1.41421356237312, 1.22474487139162, 0 ! 10
DATA 2.96944901586351, 2.91278116659653, 2.48989828488292, 0 ! 17
DATA 1.39896632596592, 1.27427369424832, 1.20710678118656, 0 ! 08
DATA 1.6180339887499 , 1.51152262815235, 1.37638192047118, 0 ! 11
DATA 2.3176109128928 , 2.20710678118658, 2.09077027517606, 1.91421356237313 ! 15
DATA 1.34371337374461, 1.2133558000219 , 1.14261350892597, 0 ! 07
DATA 2.47801865906766, 2.32743843676637, 2.26728394222856, 0 ! 16
DATA 3.80239449985143, 3.73606797749993, 3.66854248067273, 3.44095480117809 ! 18
DATA 2.23295050941571, 2.15701985252026, 2.11803398874992, 2.06457288070678 ! 14
DATA 2.15583737511568, 2.07708965974325, 1.98091594728188, 0 ! 13
END
計算結果の諸量は 以下です 有効桁数は 13 ぐらいです。
外接球半径 = R 表面積 = S 体積 = V V/(S*R)
01 .612372435695795 1.73205080756888 .117851130197758 .111111111111111
06 1.17260393995586 12.1243556529822 2.71057599454846 .190656480332432
02 .707106781186549 3.46410161513775 .471404520791033 .192450089729876
03 .866025403784443 6 1.00000000000001 .192450089729877
12 1.77882364566394 32.4346643636149 13.5996632910746 .235714258446495
05 1 9.46410161513775 2.35702260395516 .249048742268904
04 .951056516295157 8.66025403784438 2.18169499062492 .264884824097256
09 1.40125853844408 20.6457288070676 7.66311896062467 .264884824097255
10 1.58113883008421 26.7846096908266 11.313708498985 .26714660435952
17 2.96944901586351 100.990760153102 85.0396645593756 .283572442725136
08 1.39896632596592 21.4641016151378 8.71404520791042 .290201619765406
11 1.6180339887499 29.305982844912 13.8355259362495 .291777461485733
15 2.3176109128928 61.7551724393037 41.798989873224 .292046442752428
07 1.34371337374461 19.856406460551 7.88947739997544 .295692931258246
16 2.47801865906766 72.607253034134 55.2877307581239 .307286999289469
18 3.80239449985143 174.292030342324 206.803398874998 .31204912568704
14 2.23295050941571 59.305982844912 41.6153237824984 .314250279590291
13 2.15583737511568 55.2867449584451 37.6166499627341 .315604435116589
*英語版は 計算式、数値とも変更されています。(2015年1月8日現在)
2014年7月22日
Carbon nanotube
左の 一番高さのある立体が (7,2) の カイラル型左手螺旋の模型です。
これと鏡面対象の立体も考えられます。
上へ伸ばしてゆくのは もうこれぐらいにしておこうかなと思っています。
右端のラミン材で作った立体は 以前も掲載したことのある (6,3)左手螺旋ですが、
これを作るには 諸量計算がうまくゆかず 近似値計算がやっとでした。
しかも 接合部のねじれの計算に手間取ったりと手こずりました。
今回は ねじれとしては計算せず 面の傾きとして簡略しました。

まだまだ このタイプの模型製作には 初心者なので
それほど 得意げになって伝えることはありません。
おいおい お伝えしてゆきます。
カーボンナノチューブの 両端は本来
半円球の グラフェン状シートで閉じていますが
その形状の諸量計算は 私の能力をはるかに超えていますし
完成品の形状を想像しても 作ってみたいとは思いません。
あくまでも ある一部を模した模型でいいのです。私には。
こんなに溜まってしまいました。 これらの収納は日本家屋むきではないです。

2014年7月21日
BASIC Carbon nanotube 製作道具
カイラル指数 (7,2) の カイラル型の cradle と製作途中の作品です。

以下に その諸量計算の プログラムを載せておきます。
これで コンパクトにしたつもりです。
私の考えている ロジックでは このような形になりました。
多面体や球体以上に 円柱空間の理解に苦労しました。
計算した諸量での模型製作はうまくいっているようです。
製作方法等の説明は 後日しようと思っています。
! ■ カイラルタイプの carbon nanotube 模型の諸量計算 ■
! 正三角形充填平面を その辺に沿って 山折りや谷折りを加え
! 蛇腹状 ( bellows ) に加工された平面を筒状にし
! その三角形の全ての "かど" が接する円柱との結合体を考える
! 円柱の周方向にある 三角形の辺を "底辺" とし
! 底辺に向かい合う三角形の "かど" を "上かど" とする
! 底辺の両端二点を面巾とする長平面を考える
! 円柱軸と平行で 円柱に接する平面であり "底面" とする
! 同様に ある二点が面巾となり円柱と接する長平面を "補助面" とする
! 底面の 円柱軸と平行方向を y 直角方向を x 垂直方向を z とする
! 底辺の中点の (x,y,z) を (0,0,0) とする
OPTION ANGLE RADIANS ! ラジアンで計算する
01
LET a001=7 ! n ( n > m )
LET a002=2 ! m ( m < n )
IF a002/a001=0 OR a002/a001=1 THEN
PRINT "(";a001;",";a002;")";
PRINT "計算停止 !!"
PRINT "カイラル type のみの計算をします"
STOP
END IF
LET a003=SQR(3)/2 ! 三角高 xyz
LET a004=1 ! 三角高 差
LET a005=a003+.05 ! (円柱数値調整 L)
LET a006=a003-.05 ! (円柱数値調整 S)
LET a007=a003 ! (円柱数値調整 M)
LET a008=1 ! 円柱周角チェック
LET a009=0 ! ループカウント
05
LET a007=(a005+a006)/2 ! (円柱数値調整 M)
LET a010=a001+0.5*a002 ! (nm 底辺)
LET a011=a002*a007 ! (nm 対辺)
LET a012=ATN(a011/a010) ! (nm 斜角)
!■ 以下の数値は 半径=1 として計算 ■
! 寸法は 円柱面のx方向にのみ 角度と同値
LET a013=a010/COS(a012) ! (単位底数)
LET a014=(2*PI)/a013 ! (三角底巾 xy,角 xy)
LET a015=a014*COS(a012) ! (三角底巾 x)
LET a016=a014*SIN(a012) ! 三角底巾 y
LET a017=1*SIN(a015/2)*2 ! 三角底巾 x
LET a018=ATN(a016/a017) ! nm 斜角
LET a019=SQR(a017^2+a016^2)! 三角底巾 xy
LET a020=1*COS(a015/2) ! 底央・軸寸 z
LET a021=a003*a019 ! 三角高 xyz
LET a022=a021 ! 三角高 xy
LET a023=0
10
LET a023=a023+1 ! ループカウント
LET a024=a022*SIN(a018) ! 三角高 x
LET a025=a022*COS(a018) ! 三角高 y
LET a026=ASIN(a024/1) ! 上かど傾角 xz
LET a027=a024/TAN(a026) ! 上かど・軸寸 z
LET a028=a027-a020 ! 三角高 z
LET a029=ATN(a028/a022) ! 上かど仰角
LET a030=a022/COS(a029) ! 三角高 xyz大
LET a031=a030-a021 ! 三角高 xyz差
IF ABS(a031)=a004 THEN GOTO 20 ! 三角錐底面傾き修正
LET a004=ABS(a031) ! 三角錐底面傾き修正
LET a022=a021*COS(a029) ! 三角錐底面傾き修正
GOTO 10
20
LET a009=a009+a023 ! ループカウント
LET a023=0
LET a032=a015*a001 ! n円柱周角
LET a033=(a015/2+a026)*a002 ! m円柱周角
LET a034=a032+a033 ! 円柱周角 xz
IF a008=a034 THEN GOTO 30
LET a008=a034
IF a034 < 2*PI THEN LET a005=a007 ! 円柱数値調整
IF a034 > 2*PI THEN LET a006=a007 ! 円柱数値調整
GOTO 05
30
! 三角錐底面の中心は底辺中央点 (0,0,0) からの位置関係として
LET a035=a021/3 ! 角錐底心 xyz
LET a036=a022/3 ! 角錐底心 xy
LET a037=a024/3 ! 角錐底心 x
LET a038=a025/3 ! 角錐底心 y
LET a039=a028/3 ! 角錐底心 z
LET a040=a036/TAN(a029) ! 交点・心寸 z
LET a041=a039+a020 ! 心・軸寸 z
LET a042=ATN(a040/a037) ! 心垂線仰角 xz
LET a043=ASIN(a037) ! 頂傾角 xz
LET a044=1 ! 誤差最低値の繰り返し判定
40
LET a009=a009+1
LET a045=COS(a043) ! 頂・軸寸 z
LET a046=a045-a041 ! 頂・心寸 z
LET a047=a046/TAN(a042) ! 心・頂寸 x
LET a048=a037-a047 ! 頂・央寸 x
LET a049=ASIN(a048) ! 頂傾角 xz'
LET a050=COS(a049) ! 頂・軸寸 z'
LET a051=a050-a045 ! 頂・軸寸誤差
IF a044=a051 THEN GOTO 95 ! 誤差最低値の繰り返し判定
LET a044=a051 ! 頂・軸寸誤差
LET a043=a049 ! 近似頂傾角 xz
GOTO 40
95
LET a052=ATN(a040/a038) ! 心垂線仰角 yz
LET a053=a046/TAN(a052) ! 心・頂寸 y
LET a054=a038-a053 ! 頂・央寸 y
LET a055=a046+a039 ! 頂・央寸 z
LET a056=a017/2 ! 底辺寸/2 x
LET a057=a016/2 ! 底辺寸/2 y
LET a058=a055-a028 ! 上稜寸 z
LET a059=a024-a048 ! 上稜寸 x
LET a060=a025-a054 ! 上稜寸 y
LET a061=SQR(a059^2+a060^2) ! 上稜寸 xy
LET a062=SQR(a061^2+a058^2) ! 上稜寸 xyz
LET a063=a048+a056 ! 中稜寸 x
LET a064=a054-a057 ! 中稜寸 y
LET a065=SQR(a063^2+a064^2) ! 頂・央寸 xy
LET a066=SQR(a065^2+a055^2) ! 中稜寸 xyz
LET a067=a056-a048 ! 下稜寸 x
LET a068=a054+a057 ! 下稜寸 y
LET a069=SQR(a067^2+a068^2) ! 下稜寸 xy
LET a070=SQR(a069^2+a055^2) ! 下稜寸 xyz
LET a071=ATN(a058/a059) ! 上稜面仰角
LET a072=a059/COS(a071) ! 上稜面巾寸
LET a073=ATN(a055/a063) ! 中稜面仰角
LET a074=a063/COS(a073) ! 中稜面巾寸
LET a075=ATN(a055/a067) ! 下稜面仰角
LET a076=a067/COS(a075) ! 下稜面巾寸
LET a077=ATN(a072/a060) ! 上稜面 稜角
LET a078=ATN(a059/a060) ! 底面 上稜角
LET a079=ATN(a074/a064) ! 中稜面 稜角
LET a080=ATN(a063/a064) ! 底面 中稜角
LET a081=ATN(a076/a068) ! 下稜面 稜角
LET a082=ATN(a067/a068) ! 底面 下稜角
LET a083=(PI-a080)+a078 ! 底面 上 中角
LET a084=(PI-a082)-a078 ! 底面 上 下角
LET a085=a080+a082 ! 底面 中 下角
LET a086=a083+a084+a085 ! 底面 稜角 計
LET a087=a083/2-a078 ! 上 中 接合角
LET a088=a084/2+a078 ! 上 下 接合角
LET a089=a085/2-a082 ! 中 下 接合角
LET a090=(a083/2+a084/2)/2 ! 底面 上接合角/2
LET a091=(a083/2+a085/2)/2 ! 底面 中接合角/2
LET a092=(a084/2+a085/2)/2 ! 底面 下接合角/2
PRINT "カーボンナノチューブ模型カイラル型の諸量計算"
PRINT
PRINT "カイラル指数","(";a001;",";a002;")" ! ( 7 , 2 )
PRINT "稜寸 xyz", a062/a062 ! 1 1
PRINT "直径", 2/a062 ! 4.58626952818816 4.5862695281881583678
PRINT "底辺傾角 xy", a018/PI*180 ! 12.4871457895927 12.487145789592382811
PRINT
PRINT "上稜面 仰角", a071/PI*180 ! 5.33169641703842 021/225
PRINT "上稜面 稜角", a077/PI*180 ! 12.5396942073838 054/243
PRINT "底面 上稜接合角/2",DEG(a090) ! 59.6889771264966 195/114
PRINT
PRINT "中稜面 仰角", a073/PI*180 ! 9.43804224999629 041/247
PRINT "中稜面 稜角", a079/PI*180 ! 73.3250608427073 217/065 177/053
PRINT
PRINT "下稜面 仰角", a075/PI*180 ! 12.056318130851 044/206
PRINT "下稜面 稜角", a081/PI*180 ! 48.76921965494 178/156
PRINT
PRINT "以下 軸方向を 0 度として表示"
PRINT "下 中 接合角 は 上 中 接合角側"
PRINT
PRINT "上 中 接合角",a087/PI*180 ! 47.201831336904 189/175 162/150
PRINT "上 下 接合角",a088/PI*180 ! 72.1761229160893 227/073 168/054
PRINT "下 中 接合角",a089/PI*180 ! 12.4871457895928 033/149
END
2014年7月17日
Carbon nanotube 製作道具
カイラル指数 (4,4) の アームチェア型の cradle の製作説明をします。
下の諸量は 以前お伝えした BASIC での計算結果です。
カイラル指数 ( 4 , 4 )
稜寸 1
外接円柱直径 3.88538618247263
長斜面仰角 7.58565860342018
短斜面仰角 14.914341396582
短斜面稜開き角/2 59.1425987847417
底面稜接合角 60
アームチェア型は 稜部品全ての接合角が
60 度 + 60 度の 120 度になっています。
そのため 三つの cradle は三角定規を使って 切断加工の角度が得られます。
左の立体は 縦を周方向 横を軸方向にむけています。
それと同じ方向に部材ができる cradle を組み合わせて載せています。
上の二つの cradle は 14.91 度 の傾きを 軸に沿ってつけています。
二つの稜の開き角の 1/2 が 59.14 度です。
下の cradle は7.59 度で周方向に角度をつけています。

整数変換 リスト
60° = 194 / 112 59.14° = 159 / 095 14.91° = 057 / 214 7.59° = 033 / 248
2013年1月14日 諸量の計算プログラム 2 の basic で 変換できます。
IF a08>180 THEN GOTO 100 ! 短いほうが 180以下になるまで計算しない
の a08>180 を a08>a03 に 変えれば
250 × 180 の 大きさも変えられます。
2014年7月16日
Carbon nanotube 製作道具
ジグザグ型 (8,0) Zigzag の 模型の製作途中の画像です。
下画面上中ほどに 三つの逆 Y 字状の部品unit の組み合わせで立体が完成します。
逆Y字の 縦方向の部品が 上稜で 左右下に開いた二つの部品が下稜です。
その方向のまま上に 一つ 下に二つの unit を結合して
上右のサークル状に並べると 形状が解ってきます。
そして 向きを合わせながら 逆Y字部品unit を接合してゆきます。
画像下の三つの治具でこれらの 稜部品を作ります。
画像を左クリックすると 拡大されます。

下の図で 求める形に成形する治具を 結合方向に合わせて 組み合わせています。
このままの状態で部品結合すると凸面が逆になっています。
左下の治具が 右下稜を 右下が左下稜を作ります。
逆 Y 字状の部品unit を製作するときに 三つの部品それぞれに色分けなどをして
くれぐれも間違いのないように注意が必要です。
治具の傾斜のつけ方に 今まで説明してきた多面体のとは 違う特徴があります。
それは接合集中点方向ではなく 縦軸方向に傾斜していることです。
これは 球座標ではなく円柱座標を扱っているからです。
下の画像は 三つの cradle を作っているところです。
グラフ用紙に左右から59.59 度( 247/145 )の傾線を引き
中心点を通る縦線を描いています。
縦線に沿って 正四角形を59.59 度にカットした成型ボード
MDF(medium density fiberboard) を切断面を合わせて置き
斜線に 沿わせています。上稜用 cradle です。
角材を固定する溝の傾斜は0 度です。
下二つの cradle は左右対称に作ろうとしています。
60 度にカットした二つの ボードを 縦線と斜線にあわせています。
底稜の接合開き角/2 はすべてのタイプで 60 度以上なので 調整できます。
61.30 度にカットした縁に平行な溝をつけたボードを
縦線方向に沿って 11.25 度傾斜させて その上に接着しています。

下左画像は11.25 度の傾斜面をつくる アルミ板棒で
その右とその上は三角定規で 60 度の分割線をもとに加工します。
他の二つの 四角形の一つは 61.30 度 ( 179/098 )
他は 59.59 度の加工です。

一つの稜部品は 同一の cradle 上で
両端の接合面を 180 度回転対象に加工します。
2014年7月11日
<
1
2
3
4
5
6
7
8
9
10
11
12
13
>

















