ポーカーの確率
05[3,4,3,4] Compounds ポーカーの確率 多面体
下画像は [ 3,4,3,4 ] と その双対多面体を合体させた複合多面体です。
5×5mm の角材を用いて 以前お伝えしていた方法よりも 簡易な作業で作っています。
思いつくまま 制作方法を載せてゆこうと思っています。
いま この記事を入力しているＰＣは 二万円ほどで買った 新品のラップトップＰＣ で
バッタものと いわれそうですが ＯＳはＷｉｎｄｏｗｓ１０です。
ポーカーの確率計算をさせると 三分弱です。
以前のＰＣは 32秒で output なので 比較になりませんが 立ち上がりが 早く
Google関連アプリや 十進BASIC 多倍長電卓LM LibreOffice などのフリーソフトの使用で満足しています。
これから [ 3,4,3,4 ] 複合多面体 について少しずつ載せてゆくつもりです。
2019年11月23日
04[3,3,3,3,3] ポーカーの確率 多面体 製作道具
[3,3,3,3,3] 正二十面体 Icosahedron の 板棒での製作についてお伝えします。
前回までの [5,5,5] の説明を 理解されているものとして 説明します。
[5,5,5] と同じ大きさにしようとしています。
[5,5,5] の稜寸 は 30mm でしたので
面芯寸 1.11 × 30 × 2 で 高さは 約 67mm てした。
[3,3,3,3,3] の 面芯寸は 稜寸 1 に対して 約 0.756 なので
[3,3,3,3,3] の稜寸 は 67 / 2 / 0.756 で 約 44mm となります。
治具の加工角度は 90 – 31.72 で 約 58.28 度です。
直角を挟む二辺の 比としては 233/144 もしくは 288/178 が近似値です。
下画像 中ほどが その治具と 完成品です。
部材と部材の接合部分は 正五角形の筒状の空洞ができるようにします。
あとは正三角形に正三角形を次々と付けてゆくだけです。
三十枚の部材全部の両端に 合成ゴム系接着剤を塗布し
最初に塗った部材から 順次接着してゆけば あっけなく完成です。
画像右に電卓が二つ写っています。
上が Casio FX-915 で 三十年ほど前に買ったものです。
ソーラーバッテリーを電源とし 今も正常ですが
薄型のため 入力操作に 円滑さは不足しています。
ポーガーの確率計算で 組み合わせの数 52 C の 5 で
2598960 の 値が 簡単に 出てきたのに感激したのを覚えています。
下は 現在活用している Canon F-502G です。
今 最もリーズナブルに 購入できる 関数電卓の一つです。
2016年1月18日
BASIC Dürer’s solid ポーカーの確率 多面体
レオナルド・ダ・ヴィンチ Leonardo da Vinci (1452-1519) と
同時代に ドイツで活躍した
アルブレヒト・デューラー Albrecht Dürer (1471-1528)
の銅版画 メランコリア I (Melencolia I) の中にある
特殊な八面体の製作をしようと思っています。
http://de.wikipedia.org/wiki/Albrecht_D%C3%BCrer 参照
本来なら 作品を完成してから 製作方法を伝えるべきですが
やっと 諸量の計算ができたところです。
早く お伝えしようと思い 作ったばかりの BASIC のプログラムを
載せておきます。計算方法の思い違いがあるかもしれませんが
実際に作品を作ってゆけば 発見できるでしょう。
この多面体の諸量については諸説あるようですが
石津秀子さんの 論文を参考にさせていただきました。
http://www.seijo.ac.jp/pdf/falit/188/188-4.pdf
!! コピー開始
! メランコリア I (Melencolia I) の八面体の製作に
! 必要な諸量の計算 <試案>
! 菱形の鋭角を 72度とする
! 菱形の短いほうの対角線を 1とする
! 短いほうの対角線を底とする二等辺三角形を考える
! この二等辺三角形で
! 底を周方向とする二つの三角錐と一つの反角柱を作る
! 二つの三角錐に反角柱を挟んで 平行六面体を作り
! 長方向の両端をカットした形状を作る
! 八面体は球に外接するとして計算
OPTION ANGLE DEGREES
LET m001=sqr(3)/6
LET m002=sqr(3)/3
LET m003=72 ! 72 菱形鋭角
LET m004=0.5/tan(m003/2) ! .688190960235587 対角線長寸/2
LET m005=sqr(m004^2-m001^2) ! .62471870823327 三角錐の高さ 反角柱の高さ
LET m006=sqr((m002)^2+m005^2) ! .85065080835204 稜寸
LET m007=acos((m002)/m006) ! 47.2566160617882 三角錐の稜の仰角
LET m008=sqr(m002^2+(m005/2)^2) ! .656431031744764 反角柱の外接球半径
LET m009=atn((m005/2)/m002) ! 28.4143751956601 反角柱の高さ巾角/2
LET m010=m007+m009 ! 75.6709912574483 稜の球内侵入角度
LET m011=m008*sin(90-m010)*2 ! .324919696232906 三角錐のカット残の稜寸
LET m012=m006-m011 ! .525731112119134 切り離しする三角錐の稜寸
LET m013=m012/m011 ! 1.6180339887499 切り分け稜寸比 (黄金比)
LET m014=m012*sin(m003/2)*2 ! .618033988749895 カット面三角の辺寸
LET m015=asin((m006/2)/m008) ! 40.3861775591967 長稜巾角/2
LET m016=asin((m011/2)/m008) ! 14.3290087425517 短稜巾角/2
LET m017=asin((m014/2)/m008) ! 28.0831980645294 底稜巾角/2
LET m018=90-m015 ! 49.6138224408033 長稜端角
LET m019=90-m016 ! 75.6709912574483 短稜端角
LET m020=90-m017 ! 61.9168019354706 底稜端角
LET m021=90+m003/2 ! 126 五角底角
LET m022=(90-m003/2)*2 ! 108 菱形鈍角
LET m023=90-m018 ! 40.3861775591967 長稜仰角
LET m024=m006*cos(m023) ! .647936163294299 長稜投影寸
LET m025=asin(0.5/m024)*2 ! 101.010156834313 長・長稜開き角
LET m026=(360-m025)/2 ! 129.494921582844 長・短稜開き角
LET m027=90-m019 ! 14.3290087425517 短稜仰角
LET m028=90-m020 ! 28.0831980645294 底稜仰角
LET m029=cos(m028) ! .882264951894171 底稜投影縮小比
LET m030=asin(0.5/m029)*2 ! 69.0440756710915 底・底稜開き角
LET m031=(360-m030)/2 ! 145.477962164454 底・短稜開き角
LET m032=m005+m011*cos(m003/2)*2! 1.1504498203524 八面体長寸
LET m033=(1+sqr(5))/2 ! 1.61803398874989 黄金比
LET m034=atn(1/m033)*2 ! 63.4349488229222 黄金比の鋭角
LET m035=sqr(2) ! 1.4142135623731 白銀比
LET m036=atn(1/m035)*2 ! 70.5287793655091 白銀比の鋭角
PRINT "《メランコリア》の八面体"
PRINT "菱形対角線短寸",1 ! 1
PRINT "菱形対角線長寸",m004*2 ! 1.37638192047117
PRINT "菱形鋭角" ,m003 ! 72
PRINT "長稜寸" ,m006 ! .85065080835204
PRINT "短稜寸" ,m011 ! .324919696232906
PRINT "底稜寸" ,m014 ! .618033988749895
PRINT "長稜仰角" ,m023 ! 40.3861775591967
PRINT "短稜仰角" ,m027 ! 14.3290087425517
PRINT "底稜仰角" ,m028 ! 28.0831980645294
PRINT "長・長稜開き角/2",m025/2 ! 50.5050784171565
PRINT "長・短稜開き角/2",m026/2 ! 64.747460791422
PRINT "底・底稜開き角/2",m030/2 ! 34.5220378355458
PRINT "底・短稜開き角/2",m031/2 ! 72.738981082227
PRINT "八面体長寸" ,m032 ! 1.1504498203524
PRINT "外接球直径",m008*2 ! 1.31286206348953
PRINT
PRINT "参考数値"
PRINT "黄金比" , "1 :" ;m033 ! 1 : 1.61803398874989
PRINT "黄金比菱形の鋭角" ,m034 ! 63.4349488229222
PRINT "白銀比" , "1 :" ;m035 ! 1 : 1.4142135623731
PRINT "白銀比菱形の鋭角" ,m036 ! 70.5287793655091
END ! コピー終わり
以下は 整数比に変換した値です
.85065080835204 131 / 154
.324919696232906 77 / 237
.618033988749895 144 / 233
40.3861775591967 131 / 154
14.3290087425517 47 / 184
28.0831980645294 127 / 238
50.5050784171565 182 / 150
64.747460791422 212 / 100
34.5220378355458 119 / 173
72.738981082227 177 / 55
追伸
新しいパソコンに買い替えてこのブログを作っています。
以前お伝えした ポーカーの確率計算のプログラムを
このパソコンで run してみました。すると 32秒で output です。
以前は 半日もかかったのに
隔世の感を 新たにしているところです。
2014年1月25日
久しぶりの投稿です。
ブログの作成を 休止してはいません。
お伝えする内容が まだ整っていません。
今まで私が作った BASIC のプログラムで 気に入っているものを 載せておきます。
バソコンの黎明期頃に作ったプログラムの リメイク版です。
当時は 計算結果がでるまで 12時間ほどかかりました。
今は 数分ほどです。
ポーカー役手を全数チェックするものです。
! 以下をコピーして実行してください。
! フリーウエアー 十進BASIC でプログラム ! http://hp.vector.co.jp/authors/VA008683/ を参照 ! http://hp.vector.co.jp/authors/VA008683/english/index.htm 英語版 ! ポーカーの確率計算 OPTION BASE 0 DIM A(52,1) LET TT$=TIME$ LET C4C=0 LET CfH=0 LET C3C=0 LET C2P=0 LET C1P=0 LET RSF=0 LET SFL=0 LET FLS=0 LET STR=0 LET NP=0 LET B=0 LET CNT1=0 LET CNT2=0 ! ５２枚の札を１～５２の番号付けをする ! 種類の区別は 0001, 0010, 0100, 1000 の4通り ! 数字の区別は 0000000000001, 0000000000010 ～ 1000000000000 の 13通り ! 種類と数字のペア52通り として 登録 FOR I=0 TO 3 FOR J=0 TO 12 LET B=B+1 LET A(B,0)=10^I LET A(B,1)=10^J NEXT J NEXT I ! ５２枚の札を１～５２の番号付けして、ゼロと重複を認めない５桁の５３進数 ! として表現し、それぞれの５桁の数列の中で、上位にある数は下位にある数 ! より小さいという条件で数列をつくり ２５９８９６０通り作成 ! ５枚の札の組み合わせの特徴の表現は ＜例えばＲＳＦ＞ ! 種類 0005, 0050, 0500, 5000 と 数字 1000000001111 の ４種の組合せ PRINT CNT1,TT$ FOR K= 1 TO 52-4 FOR L=K+1 TO 52-3 FOR M=L+1 TO 52-2 FOR N=M+1 TO 52-1 FOR O=N+1 TO 52 LET AA =A(K,0)+A(L,0)+A(M,0)+A(N,0)+A(O,0)+9*10^4 LET BB =A(K,1)+A(L,1)+A(M,1)+A(N,1)+A(O,1)+9*10^13 LET AA$=STR$(AA) LET BB$=STR$(BB) LET A$=AA$(2:5) LET B$=BB$(2:14) LET X=POS(B$,"4",1) ! 同じ数字が４枚あるか IF X > 0 THEN LET C4C=C4C+1 !4カード GOTO 1000 END IF LET Y=POS(B$,"3",1) IF Y > 0 THEN GOTO 900 ELSE GOTO 901 900 REM IF POS(B$,"2",1) >0 THEN LET CFH=CFH+1 !フルハウス GOTO 1000 END IF LET C3C=C3C+1 !3カード GOTO 1000 901 REM LET Z=POS(B$,"2",1) IF Z > 0 THEN GOTO 902 ELSE GOTO 903 902 REM IF POS(B$,"2",Z+1) >0 THEN LET C2P=C2P+1 !2ペアー GOTO 1000 END IF LET C1P=C1P+1 !1ペアー GOTO 1000 903 REM 1枚も同じ数が無い数列 LET ZZ=POS(A$,"5",1) LET ZX=POS(B$,"1",1) LET ZX$=B$(ZX+1:ZX+4) LET ZY$=B$(10:13) IF ZZ=0 THEN GOTO 904 ELSE GOTO 905 904 REM IF ZX$="1111" THEN LET STR=STR+1 GOTO 1000 END IF IF ZX=1 AND ZY$="1111" THEN LET STR=STR+1 GOTO 1000 END IF LET NP =NP+1 GOTO 1000 905 REM IF ZX$="1111" THEN LET SFL=SFL+1 GOTO 1000 END IF IF ZX=1 AND ZY$="1111" THEN LET RSF=RSF+1 GOTO 1000 END IF LET FLS=FLS+1 1000 REM LET CNT1=CNT1+1 LET CNT2=CNT2+1 IF CNT2=100000 THEN LET CNT2 = 0 PRINT CNT1,TIME$ END IF NEXT O NEXT N NEXT M NEXT L NEXT K PRINT CNT1,TIME$ PRINT "Royal flush =",RSF PRINT "Straight flush =",SFL PRINT "Four of a kind =",C4C PRINT "Full house =",CFH PRINT "Flush =",FLS PRINT "Straight =",STR PRINT "Three of a kind =",C3C PRINT "Two pair =",C2P PRINT "One pair =",C1P PRINT "No pair =",NP PRINT "Total =",CNT1 END ! コピー終わり 私のパソコンでは RUN して 1分 34秒後に 以下の OUT PUT がありました。 Royal flush = 4 Straight flush = 36 Four of a kind = 624 Full house = 3744 Flush = 5108 Straight = 10200 Three of a kind = 54912 Two pair = 123552 One pair = 1098240 No pair = 1302540 Total = 2598960
2013年6月25日
14[3,4,5,4] Excel ポーカーの確率 多面体 諸量
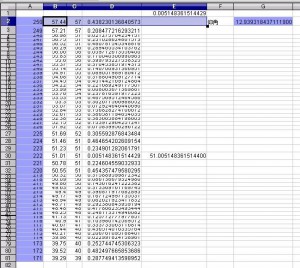
今度は 角度をグラフ用紙に表示するための整数比換算のエクセル画面です。
計算式は以下です。 後日投稿のリメイク版もあります。
[ 3,4,5,4 ] に限らず
プラトン多面体や アルキメデス多面体 など
18種類ある値の計算ができます。
1行目 E 列 =SMALL(D2:D81,1) 2行目 B 列 =TAN(RADIANS($G$2))*A2 2行目 C 列 =ROUND( TAN(RADIANS($G$2))*A2,0) 2行目 D 列 =ABS(B2-C2) 2行目 E 列 =IF(D2=$E$1,B2," ") 2行目 B 列から E列までを選択し セルの右下にポインタを合わせ 「＋」を下方(81行まで)にドラッグする[オートフィル]を行います。 A列の 2行目に 250 A列の 3行目に 249 を入れ 250と249を選択し 81行目までオートフィルします。 *2015年3月20日変更2行目 G列に 12.9393184371119 を入れると
2012年7月12日
