14[3,4,5,4] Excel ポーカーの確率 多面体 諸量
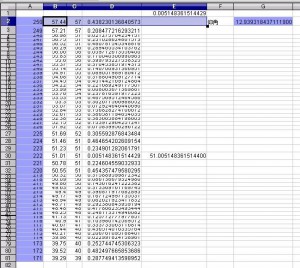
今度は 角度をグラフ用紙に表示するための整数比換算のエクセル画面です。
計算式は以下です。 後日投稿のリメイク版もあります。
[ 3,4,5,4 ] に限らず
プラトン多面体や アルキメデス多面体 など
18種類ある値の計算ができます。
1行目 E 列 =SMALL(D2:D81,1)
2行目 B 列 =TAN(RADIANS($G$2))*A2
2行目 C 列 =ROUND( TAN(RADIANS($G$2))*A2,0)
2行目 D 列 =ABS(B2-C2)
2行目 E 列 =IF(D2=$E$1,B2," ")
2行目 B 列から E列までを選択し セルの右下にポインタを合わせ
「+」を下方(81行まで)にドラッグする[オートフィル]を行います。
A列の 2行目に 250
A列の 3行目に 249 を入れ
250と249を選択し
81行目までオートフィルします。 *2015年3月20日変更
2行目 G列に 12.9393184371119 を入れると
上に掲載の画面と同じ表示結果になります。
この数字は 斜方20・12面体 [ 3,4,5,4 ]の製作部品の仰角で
A列の250 から 171の範囲での計算で
1行目 E列の数値が 最も近似の角度表示をする整数比の 誤差です。
30行目 E列の数値の 222 と 51 がその答えだということです。
A列の数字を251行まで入れて 1までで計算すると
74 対 17.001 が一番誤差が少なく 次は 148 対 34.003 で
三番目に 222 対 51.005 なのですが
エクセルで 関数計算的な数値処理をする場合 煩雑なこともありますが
関数電卓で 数値処理をするより遥かに便利でした (多面体関連についてですが)。
今は フリーウェアーソフトの 十進BASIC を使っています。
http://hp.vector.co.jp/authors/VA008683/ を参照
このソフトがなかったら 多面体製作が趣味になっていなかったかも知れません。
そのほか
ポーカーの役の確率計算を 順列や組み合わせを用いた論理計算ではなく
全数チェックで しかも短時間で調べることもできました。
2012年7月12日
14[3,4,5,4] Excel 多面体 諸量

斜方20・12面体 [ 3,4,5,4 ] の諸量を エクセルで計算しています。
画像をクリックすると 大きな画面になります。
画像形式が JPGなので 表計算ソフトに文字を移せませんが
最後のほうに記しています文字や計算式を エクセルやそれ相当のソフトに
コピー&ドロップすれば少しは作業性がよくなり走らすことができます。
*注 後日投稿(2015年 05月24日)のリメイク版もあります。そちらをお勧めします。
カラーの背景のセルのみ 数字の手入力部分です。
これで一般的に 正多面体と準正多面体 のデータが計算できます。
左上の 個数 角数の入力欄は 一つの頂に集まる正多角形の 数と角数を入力します。
必ず三行の入力が必要です。
立方八面体[ 3,4,3,4 ]では 三角形が一個と四角形が二個 それにまた三角形が一個と
入力できますが 三角形が二個 四角形が一個 そして四角形が一個でもOKです。
もっとシンプルな体裁にできるのですが IF文を使ったり 式が複雑になります。
もう一つのカラーの背景の 974607762378170 となっている入力欄に
866025403784438の 数字を入れると ←*注
10行目のF列に 360.000000000000000となり
立方八面体[ 3,4,3,4 ] の計算完了で 仰角や接合角がわかります。
計算手順は
個数 角数 個数 角数
1 3 2 3
2 4 1 4
1 3 とか 1 4 などと入力し
最初は 12行目 B列 に 8 を入れ 後のB列はすべてゼロにして
10行目のF列の表示が 360以上の数値になり
7を入れると 今回は計算異常の表示が出ますが 気にせず
その数より 大であるということであり
もとの数字8にもどし つぎの下の 0 を変更します。
ある数字を入れると 360以上になり
その数より1つ上の数を入れると 360以下になる場合
もとの数字にもどし 下の欄の数字の入力をします その繰り返しです。(2015年5月22日 変更)
今までは 天下り的な数値報告をしていましたので
その根拠を伝えたかったのですが
文章が長くなったり 理解しにくい点があるかも知れません お許しください。
コピー&ドロップする内容です
C列からG列までは 書式設定で 小数点以下の桁数を 15にしています。
1 行目 A 列 → 個数
1 行目 B 列 → 角数
1 行目 C 列 → 頂角度(R)
1 行目 D 列 → 頂角度(D)
1 行目 E 列 → 側角度(R)
1 行目 F 列 → 側角度(D)
1 行目 G 列 → 角底寸/2
2 行目 C 列 → =(PI()/2-PI()/B2)*2
2 行目 D 列 → =DEGREES(C2)
2 行目 E 列 → =PI()/B2
2 行目 F 列 → =DEGREES(E2)
2 行目 G 列 → =COS(E2)
2 行目の C 列から G 列まで
セルの右下にポインタを合わせ「+」を
4 行目までドラッグする [オートフィル]機能 を使います。
6 行目 C 列 → 底面 側角度(R)
6 行目 D 列 → 底面 頂角度(R)
6 行目 E 列 → 底面 頂角度(D)
6 行目 F 列 → 底面 総頂角度(D)
6 行目 G 列 → 接合角
7 行目 B 列 → =B2
7 行目 C 列 → =ACOS(G2/$C$27)
7 行目 D 列 → =(PI()/2-C7)*2
7 行目 E 列 → =DEGREES(D7)
7 行目 F 列 → =E7*A2
7 行目 G 列 → =E7/2
7 行目の B 列から G 列まで
セルの右下にポインタを合わせ「+」を
9 行目までドラッグする [オートフィル]機能 を使います。
10 行目 F 列 → =SUM(F7:F9)
12 行目 C 列 → =B12*1/10^A12
12 行目の C 列 の
セルの右下にポインタを合わせ「+」を
26 行目までドラッグする [オートフィル]機能 を使います。
27 行目 C 列 → =SUM(C12:C26)
13 行目 E 列 → 仰角
14 行目 E 列 → =DEGREES(ACOS(C27))
17 行目 E 列 → 稜芯寸
18 行目 E 列 → =0.5*C27/SQRT(1-C27^2)
21 行目 E 列 → 頂芯寸
22 行目 E 列 → =0.5/SQRT(1-C27^2) *2015年3月20日変更
*注
"951056516295153の 数字を入れると" の表現でした (2015年5月22日 まで)
これは 立方八面体[ 3,4,3,4 ] の値ではなく 20・12面体[3,5,3,5] の値でした
混乱をおかけしたことを お詫びし 訂正いたします。
2012年7月9日




