Carbon nanotube
Carbon nanotube
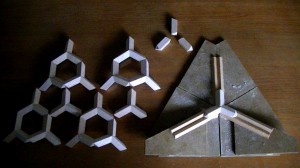
左の 一番高さのある立体が (7,2) の カイラル型左手螺旋の模型です。
これと鏡面対象の立体も考えられます。
上へ伸ばしてゆくのは もうこれぐらいにしておこうかなと思っています。
右端のラミン材で作った立体は 以前も掲載したことのある (6,3)左手螺旋ですが、
これを作るには 諸量計算がうまくゆかず 近似値計算がやっとでした。
しかも 接合部のねじれの計算に手間取ったりと手こずりました。
今回は ねじれとしては計算せず 面の傾きとして簡略しました。

まだまだ このタイプの模型製作には 初心者なので
それほど 得意げになって伝えることはありません。
おいおい お伝えしてゆきます。
カーボンナノチューブの 両端は本来
半円球の グラフェン状シートで閉じていますが
その形状の諸量計算は 私の能力をはるかに超えていますし
完成品の形状を想像しても 作ってみたいとは思いません。
あくまでも ある一部を模した模型でいいのです。私には。
こんなに溜まってしまいました。 これらの収納は日本家屋むきではないです。

2014年7月21日
BASIC Carbon nanotube 製作道具
カイラル指数 (7,2) の カイラル型の cradle と製作途中の作品です。

以下に その諸量計算の プログラムを載せておきます。
これで コンパクトにしたつもりです。
私の考えている ロジックでは このような形になりました。
多面体や球体以上に 円柱空間の理解に苦労しました。
計算した諸量での模型製作はうまくいっているようです。
製作方法等の説明は 後日しようと思っています。
! ■ カイラルタイプの carbon nanotube 模型の諸量計算 ■
! 正三角形充填平面を その辺に沿って 山折りや谷折りを加え
! 蛇腹状 ( bellows ) に加工された平面を筒状にし
! その三角形の全ての "かど" が接する円柱との結合体を考える
! 円柱の周方向にある 三角形の辺を "底辺" とし
! 底辺に向かい合う三角形の "かど" を "上かど" とする
! 底辺の両端二点を面巾とする長平面を考える
! 円柱軸と平行で 円柱に接する平面であり "底面" とする
! 同様に ある二点が面巾となり円柱と接する長平面を "補助面" とする
! 底面の 円柱軸と平行方向を y 直角方向を x 垂直方向を z とする
! 底辺の中点の (x,y,z) を (0,0,0) とする
OPTION ANGLE RADIANS ! ラジアンで計算する
01
LET a001=7 ! n ( n > m )
LET a002=2 ! m ( m < n )
IF a002/a001=0 OR a002/a001=1 THEN
PRINT "(";a001;",";a002;")";
PRINT "計算停止 !!"
PRINT "カイラル type のみの計算をします"
STOP
END IF
LET a003=SQR(3)/2 ! 三角高 xyz
LET a004=1 ! 三角高 差
LET a005=a003+.05 ! (円柱数値調整 L)
LET a006=a003-.05 ! (円柱数値調整 S)
LET a007=a003 ! (円柱数値調整 M)
LET a008=1 ! 円柱周角チェック
LET a009=0 ! ループカウント
05
LET a007=(a005+a006)/2 ! (円柱数値調整 M)
LET a010=a001+0.5*a002 ! (nm 底辺)
LET a011=a002*a007 ! (nm 対辺)
LET a012=ATN(a011/a010) ! (nm 斜角)
!■ 以下の数値は 半径=1 として計算 ■
! 寸法は 円柱面のx方向にのみ 角度と同値
LET a013=a010/COS(a012) ! (単位底数)
LET a014=(2*PI)/a013 ! (三角底巾 xy,角 xy)
LET a015=a014*COS(a012) ! (三角底巾 x)
LET a016=a014*SIN(a012) ! 三角底巾 y
LET a017=1*SIN(a015/2)*2 ! 三角底巾 x
LET a018=ATN(a016/a017) ! nm 斜角
LET a019=SQR(a017^2+a016^2)! 三角底巾 xy
LET a020=1*COS(a015/2) ! 底央・軸寸 z
LET a021=a003*a019 ! 三角高 xyz
LET a022=a021 ! 三角高 xy
LET a023=0
10
LET a023=a023+1 ! ループカウント
LET a024=a022*SIN(a018) ! 三角高 x
LET a025=a022*COS(a018) ! 三角高 y
LET a026=ASIN(a024/1) ! 上かど傾角 xz
LET a027=a024/TAN(a026) ! 上かど・軸寸 z
LET a028=a027-a020 ! 三角高 z
LET a029=ATN(a028/a022) ! 上かど仰角
LET a030=a022/COS(a029) ! 三角高 xyz大
LET a031=a030-a021 ! 三角高 xyz差
IF ABS(a031)=a004 THEN GOTO 20 ! 三角錐底面傾き修正
LET a004=ABS(a031) ! 三角錐底面傾き修正
LET a022=a021*COS(a029) ! 三角錐底面傾き修正
GOTO 10
20
LET a009=a009+a023 ! ループカウント
LET a023=0
LET a032=a015*a001 ! n円柱周角
LET a033=(a015/2+a026)*a002 ! m円柱周角
LET a034=a032+a033 ! 円柱周角 xz
IF a008=a034 THEN GOTO 30
LET a008=a034
IF a034 < 2*PI THEN LET a005=a007 ! 円柱数値調整
IF a034 > 2*PI THEN LET a006=a007 ! 円柱数値調整
GOTO 05
30
! 三角錐底面の中心は底辺中央点 (0,0,0) からの位置関係として
LET a035=a021/3 ! 角錐底心 xyz
LET a036=a022/3 ! 角錐底心 xy
LET a037=a024/3 ! 角錐底心 x
LET a038=a025/3 ! 角錐底心 y
LET a039=a028/3 ! 角錐底心 z
LET a040=a036/TAN(a029) ! 交点・心寸 z
LET a041=a039+a020 ! 心・軸寸 z
LET a042=ATN(a040/a037) ! 心垂線仰角 xz
LET a043=ASIN(a037) ! 頂傾角 xz
LET a044=1 ! 誤差最低値の繰り返し判定
40
LET a009=a009+1
LET a045=COS(a043) ! 頂・軸寸 z
LET a046=a045-a041 ! 頂・心寸 z
LET a047=a046/TAN(a042) ! 心・頂寸 x
LET a048=a037-a047 ! 頂・央寸 x
LET a049=ASIN(a048) ! 頂傾角 xz'
LET a050=COS(a049) ! 頂・軸寸 z'
LET a051=a050-a045 ! 頂・軸寸誤差
IF a044=a051 THEN GOTO 95 ! 誤差最低値の繰り返し判定
LET a044=a051 ! 頂・軸寸誤差
LET a043=a049 ! 近似頂傾角 xz
GOTO 40
95
LET a052=ATN(a040/a038) ! 心垂線仰角 yz
LET a053=a046/TAN(a052) ! 心・頂寸 y
LET a054=a038-a053 ! 頂・央寸 y
LET a055=a046+a039 ! 頂・央寸 z
LET a056=a017/2 ! 底辺寸/2 x
LET a057=a016/2 ! 底辺寸/2 y
LET a058=a055-a028 ! 上稜寸 z
LET a059=a024-a048 ! 上稜寸 x
LET a060=a025-a054 ! 上稜寸 y
LET a061=SQR(a059^2+a060^2) ! 上稜寸 xy
LET a062=SQR(a061^2+a058^2) ! 上稜寸 xyz
LET a063=a048+a056 ! 中稜寸 x
LET a064=a054-a057 ! 中稜寸 y
LET a065=SQR(a063^2+a064^2) ! 頂・央寸 xy
LET a066=SQR(a065^2+a055^2) ! 中稜寸 xyz
LET a067=a056-a048 ! 下稜寸 x
LET a068=a054+a057 ! 下稜寸 y
LET a069=SQR(a067^2+a068^2) ! 下稜寸 xy
LET a070=SQR(a069^2+a055^2) ! 下稜寸 xyz
LET a071=ATN(a058/a059) ! 上稜面仰角
LET a072=a059/COS(a071) ! 上稜面巾寸
LET a073=ATN(a055/a063) ! 中稜面仰角
LET a074=a063/COS(a073) ! 中稜面巾寸
LET a075=ATN(a055/a067) ! 下稜面仰角
LET a076=a067/COS(a075) ! 下稜面巾寸
LET a077=ATN(a072/a060) ! 上稜面 稜角
LET a078=ATN(a059/a060) ! 底面 上稜角
LET a079=ATN(a074/a064) ! 中稜面 稜角
LET a080=ATN(a063/a064) ! 底面 中稜角
LET a081=ATN(a076/a068) ! 下稜面 稜角
LET a082=ATN(a067/a068) ! 底面 下稜角
LET a083=(PI-a080)+a078 ! 底面 上 中角
LET a084=(PI-a082)-a078 ! 底面 上 下角
LET a085=a080+a082 ! 底面 中 下角
LET a086=a083+a084+a085 ! 底面 稜角 計
LET a087=a083/2-a078 ! 上 中 接合角
LET a088=a084/2+a078 ! 上 下 接合角
LET a089=a085/2-a082 ! 中 下 接合角
LET a090=(a083/2+a084/2)/2 ! 底面 上接合角/2
LET a091=(a083/2+a085/2)/2 ! 底面 中接合角/2
LET a092=(a084/2+a085/2)/2 ! 底面 下接合角/2
PRINT "カーボンナノチューブ模型カイラル型の諸量計算"
PRINT
PRINT "カイラル指数","(";a001;",";a002;")" ! ( 7 , 2 )
PRINT "稜寸 xyz", a062/a062 ! 1 1
PRINT "直径", 2/a062 ! 4.58626952818816 4.5862695281881583678
PRINT "底辺傾角 xy", a018/PI*180 ! 12.4871457895927 12.487145789592382811
PRINT
PRINT "上稜面 仰角", a071/PI*180 ! 5.33169641703842 021/225
PRINT "上稜面 稜角", a077/PI*180 ! 12.5396942073838 054/243
PRINT "底面 上稜接合角/2",DEG(a090) ! 59.6889771264966 195/114
PRINT
PRINT "中稜面 仰角", a073/PI*180 ! 9.43804224999629 041/247
PRINT "中稜面 稜角", a079/PI*180 ! 73.3250608427073 217/065 177/053
PRINT
PRINT "下稜面 仰角", a075/PI*180 ! 12.056318130851 044/206
PRINT "下稜面 稜角", a081/PI*180 ! 48.76921965494 178/156
PRINT
PRINT "以下 軸方向を 0 度として表示"
PRINT "下 中 接合角 は 上 中 接合角側"
PRINT
PRINT "上 中 接合角",a087/PI*180 ! 47.201831336904 189/175 162/150
PRINT "上 下 接合角",a088/PI*180 ! 72.1761229160893 227/073 168/054
PRINT "下 中 接合角",a089/PI*180 ! 12.4871457895928 033/149
END
2014年7月17日
Carbon nanotube 製作道具
カイラル指数 (4,4) の アームチェア型の cradle の製作説明をします。
下の諸量は 以前お伝えした BASIC での計算結果です。
カイラル指数 ( 4 , 4 )
稜寸 1
外接円柱直径 3.88538618247263
長斜面仰角 7.58565860342018
短斜面仰角 14.914341396582
短斜面稜開き角/2 59.1425987847417
底面稜接合角 60
アームチェア型は 稜部品全ての接合角が
60 度 + 60 度の 120 度になっています。
そのため 三つの cradle は三角定規を使って 切断加工の角度が得られます。
左の立体は 縦を周方向 横を軸方向にむけています。
それと同じ方向に部材ができる cradle を組み合わせて載せています。
上の二つの cradle は 14.91 度 の傾きを 軸に沿ってつけています。
二つの稜の開き角の 1/2 が 59.14 度です。
下の cradle は7.59 度で周方向に角度をつけています。

整数変換 リスト
60° = 194 / 112 59.14° = 159 / 095 14.91° = 057 / 214 7.59° = 033 / 248
2013年1月14日 諸量の計算プログラム 2 の basic で 変換できます。
IF a08>180 THEN GOTO 100 ! 短いほうが 180以下になるまで計算しない
の a08>180 を a08>a03 に 変えれば
250 × 180 の 大きさも変えられます。
2014年7月16日
Carbon nanotube 製作道具
ジグザグ型 (8,0) Zigzag の 模型の製作途中の画像です。
下画面上中ほどに 三つの逆 Y 字状の部品unit の組み合わせで立体が完成します。
逆Y字の 縦方向の部品が 上稜で 左右下に開いた二つの部品が下稜です。
その方向のまま上に 一つ 下に二つの unit を結合して
上右のサークル状に並べると 形状が解ってきます。
そして 向きを合わせながら 逆Y字部品unit を接合してゆきます。
画像下の三つの治具でこれらの 稜部品を作ります。
画像を左クリックすると 拡大されます。

下の図で 求める形に成形する治具を 結合方向に合わせて 組み合わせています。
このままの状態で部品結合すると凸面が逆になっています。
左下の治具が 右下稜を 右下が左下稜を作ります。
逆 Y 字状の部品unit を製作するときに 三つの部品それぞれに色分けなどをして
くれぐれも間違いのないように注意が必要です。
治具の傾斜のつけ方に 今まで説明してきた多面体のとは 違う特徴があります。
それは接合集中点方向ではなく 縦軸方向に傾斜していることです。
これは 球座標ではなく円柱座標を扱っているからです。
下の画像は 三つの cradle を作っているところです。
グラフ用紙に左右から59.59 度( 247/145 )の傾線を引き
中心点を通る縦線を描いています。
縦線に沿って 正四角形を59.59 度にカットした成型ボード
MDF(medium density fiberboard) を切断面を合わせて置き
斜線に 沿わせています。上稜用 cradle です。
角材を固定する溝の傾斜は0 度です。
下二つの cradle は左右対称に作ろうとしています。
60 度にカットした二つの ボードを 縦線と斜線にあわせています。
底稜の接合開き角/2 はすべてのタイプで 60 度以上なので 調整できます。
61.30 度にカットした縁に平行な溝をつけたボードを
縦線方向に沿って 11.25 度傾斜させて その上に接着しています。

下左画像は11.25 度の傾斜面をつくる アルミ板棒で
その右とその上は三角定規で 60 度の分割線をもとに加工します。
他の二つの 四角形の一つは 61.30 度 ( 179/098 )
他は 59.59 度の加工です。

一つの稜部品は 同一の cradle 上で
両端の接合面を 180 度回転対象に加工します。
2014年7月11日
BASIC Carbon nanotube
カーボンナノチューブ carbon nanotube の
ジグザグ型 (8,0) Zigzag の 模型 について お伝えします。
下の諸量は 前回のBASIC の output です。
カイラル指数 ( 8 , 0 )
稜寸 1
かどが接する円柱直径 4.49612132172072
斜面仰角 11.25
斜面 底稜開き角 61.3004286589633
角柱面 底・縦稜開き角/2 59.5851260907253
正三角形辺寸 1.72059113972594
2013年3月9日に掲載した蜂の巣状六角形に三角形が詰まった図を
print out して手元にあるとして説明します。
山折 谷折の処理もお願いしておきます。
(8,0) Zigzag とは 三角形の底を横一直線に八つ並べた両端を接触させている
蛇腹状の柱状立体で
三角形の各かど点が 円柱に接していると考えられます。
立体の軸を上下方向に向け 三角形内の三つの辺を 逆 Y 字状にします。
三角形の底に六角形の二辺が 120度開いて付いた状態で 一周していますが
この形状が ノコギリの歯のような Zigzag な形に見えます。
稜寸とは 六角形の一辺の長さですが
逆Y字交点が 本来の位置(円柱面に接触)にあるとしての寸法です。
三つの型の形状の範囲は対称性を考慮すると
逆Y字が 0度から 30度に傾くまでで全てを表せます。
( 円柱面に投影したとしての角度)
逆Y字の三本の線を稜として 名前づけしておきます。
上の縦線を 上稜 下の斜めの線を 底稜とし
傾きがある場合上から下に向かって 上稜 中稜 下稜とします。
補助線の正三角形の辺も 傾辺 底辺とし
傾きがある場合上から下に向かって 上辺 中辺 底辺とします。
カイラル指数 (4,4) とは下辺を 4つ 上辺を 4つ 下がった点までを
一周とする立体形状を言い 傾き角度は 30度です。
その形状が アームチェアに見えるそうです。
(8,0)型の治具製作を説明する写真も用意していたのですが
字数が多くなってしまい 掲載は次回にします。
! アームチェア型諸量計算
LET b001=SQR(3)/2 ! .866025403784439 かど・底辺寸
LET b002=4 ! 4 カイラル指数 n ( n , n )
LET b003=2*pi/(b002*2) ! .785398163397448 45 底・かど巾角 xz
LET b004=(b001/2)/SIN(b003/2) ! 1.13151671922686 円柱半径 z
LET b005=(b001/2)/TAN(b003/2) ! 1.04538513758801 角柱面・軸寸 z
LET b006=b001/6 ! .144337567297407 角錐頂寸 x
LET b007=ASIN(b006/b004) ! .127909644574917 7.32868279316117 角錐頂角 xz
LET b008=b004*COS(b007) ! 1.1222730294169 頂・軸寸 z
LET b009=b008-b005 ! .07688789182889 頂・底辺寸 z
LET b010=ATN(b009/(b001/1.5)) ! .132394718561917 7.58565860342018 三角錐稜仰角
LET b011=(b001/1.5)/COS(b010) ! .5824474922628 三角錐稜寸
LET b012=ATN(b009/(b001/3)) ! .260304363136846 14.914341396582 短斜面仰角
LET b013=(b001/3)/COS(b012) ! .298739152511392 短斜面巾寸 xz
LET b014=ATN(0.5/b013) ! 1.03223307697974 59.1425987847417 短斜面稜開き角/2
LET b015=360/6 ! 60 底面稜接合角
PRINT "カイラル指数","(";b002;","; b002 ;")" ! ( 4 , 4 )
PRINT "稜寸",b011/b011 ! 1
PRINT "外接円柱直径",(b004*2)/b011 ! 3.88538618247263 237 / 61
PRINT "長斜面仰角",b010/pi*180 ! 7.58565860342016 33 / 248
PRINT "短斜面仰角",b012/pi*180 ! 14.914341396582 57 / 214
PRINT "短斜面稜開き角/2",b014/pi*180 ! 59.1425987847416 159 / 95
PRINT "底面稜接合角",b015 ! 60 194 / 112
END
2014年7月9日
BASIC Carbon nanotube
カーボンナノチューブ carbon nanotube の 模型 について お伝えします。
今回は 三つあるタイプの一つのタイプ ジグザグ型 Zigzag です。
カイラル型 Chiral と比べて
このタイプの 模型 としての諸量計算は簡単ですが
円柱座標を扱うため 球形座標以上に 説明するのが苦手です。
ひとまず 諸量計算プログラムを載せておきます。
カイラル指数 ( 8 , 0 ) とし
円柱に正八角柱の稜が接する空間として計算しています。
正八角柱の一つの面に正三角形の一辺を 周方向に置きます。
そして 上かど が円柱面に接する三角形充填面柱の 諸量計算をします。
その三角形を 底とする 三角錐の頂が 円柱に接する立体の諸量計算をする。
この三角錐の稜が ( 8 , 0 ) の稜と 合同である。
と考えて計算しています。

OPTION ANGLE DEGREES
! ジグザグ型諸量計算
! 正三角形の一辺を 1 として
LET a001=SQR(3)/2 ! .866025403784439 かど・底辺寸
LET a002=8 ! 8 カイラル指数 n ( n , 0 )
LET a003=360/a002 ! 45 底辺巾角 xz
LET a004=0.5/SIN(a003/2) ! 1.30656296487638 円柱半径 z
LET a005=0.5/TAN(a003/2) ! 1.20710678118655 角柱面・軸寸 z
LET a006=0.5*TAN(a003/4) ! .099456183689829 かど・底辺寸 z
LET a007=ASIN(a006/a001) ! 6.59451821615418 かど・底辺仰角
LET a008=a001*COS(a007) ! .860295569862972 かど・底辺寸 y
LET a009=(a001/1.5)/COS(a007) ! .581195600111762 稜寸
LET a010=a008-a009 ! .27909996975121 頂・底辺寸 y
LET a011=0.5/COS(a003/4) ! .509795579104159 頂・角柱面端寸 xz
LET a012=ATN(a011/a010) ! 61.3004286589633 斜面 底稜開き角
LET a013=ATN(0.5 /a010) ! 60.8297478185495 角柱面 底・底稜開き角/2
LET a014=(180-a013)/2 ! 59.5851260907253 角柱面 底・縦稜開き角/2
PRINT "カイラル指数","(";a002;" , 0 )" ! ( 8 , 0 )
PRINT "稜寸",a009/a009 ! 1
PRINT "かどが接する円柱直径",(a004*2)/a009 ! 4.49612132172072 243 / 54
PRINT "斜面仰角",a003/4 ! 11.25 37 / 186
PRINT "斜面 底稜開き角",a012 ! 61.3004286589633 179 / 98
PRINT "角柱面 底・縦稜開き角/2",a014 ! 59.5851260907253 247 / 145
PRINT "正三角形辺寸",1/a009 ! 1.72059113972594 234 / 136
END
2014年3月12日
Carbon nanotube

カーボンナノチューブの中の一つのタイプ、カイラルチューブの模型です。
カイラル指数 (6,3) で 左手回り螺旋です。
5×5 の角材で 20mm の三種の部品でできています。
14mm ぐらいにしたかったのですが 加工が困難でした。
ナノチューブの形状の種類は
アームチェアチューブ、ジグザグチューブ、カイラルチューブの
3種類に分けられます。
興味があっても なかなか理解しにくい といった印象が私にはありました。
そこで 以下のような図を作って 形状確認をしました。
jpgで作っています。A4でブリントアウトできます。

プリントアウトして この平らなままで円柱状にして 形状確認をしますと
正六角形 蜂の巣状の図を 円柱への投影という状態です。
それは ほとんどの稜線が 螺旋曲線になっています。
それを避けるために 以下の方法をとり用紙を加工しました。
六角形は黒の線で描写し 他の線は青で描いています。
青の線全てを 山折りにして しっかり折ります。
全て の折りが完了したら 用紙の長寸方向と平行な線を
全て しっかり谷折り状態に 折りなおします。
このように 加工した用紙で 形状確認をすると
私のように 関心はあるが もいち 理解が困難と思っていられる方も
少しは 理解が進むかもしれません。
でも これだけの作業では
六角形の六点あるかどの三つのかどが円柱に接していないこと
つまり 正六角の図面を加工し 丸めるだけでは 立体形成には無理だとも解ります。
一般に得られる概説では
平面を円柱に変形しただけの説明で終わっているように思えます。
三次元の空間の中の 円柱座標のこと また螺旋や楕円 そして
直線や捻れという概念に 理解を深める必要があると感じるようになりました。
Carbon nanotube の諸量や その計算ロジックについては
まだ お伝えする状態にはなっていません。
以前 計算し確認した諸量やロジックをもう一度 調べなおしています。
私が 参考にし 理解できる 資料に乏しく まだ自信がもてません。
そして 複雑になってしまった計算式を改良修正し 簡略化しようと思っています。
しばらく 時間がかかります。
2013年3月9日
13[3,3,3,3,5] Carbon nanotube 多面体

S形の結合部品の組合せ作業のみで迷うことなく簡単に
Pentagonal Hexecontahedron が完成しました。
簡単にとは言っても 稜部品のカットと整形には 飽きるほど単純な反復作業に耐えてきましたが。
次に何をしようかと迷っています。
今までの製作方法の説明と 諸量のデータで 正多面体 準正多面体 双対多面体 そしてそれらの複合多面体 compounds はつくれるはずです。
しかし 私の説明がうまく伝えられていればのことですが。
私自身まだ 作っていない多面体や 複合多面体がありますので
思いつくまま製作して それをお伝えしようかなと 今思っています。
一番最初のブログで お伝えするとしてまだ実行していないものがあります。
それはカーボンナノチューブ (Carbon nanotube) 模型です。
平面充填六角形の円柱座標での取り扱いという単純な作業ではなく。
平面充填三角形のかど点を 三次元の中の円柱面に投影するという説明が必要です。
またその中のタイプの spiral な形状の説明も必要となってきます。
私には大変 困難なことです。少しずつ 準備をしてゆこうと思っています。
球ではなく円柱を取り扱うため symmetry なことではかなり劣りますし。
sashimono としては歪みが生じます。
どれだけ関心のある方たちが居られるかも不安ではあります。
2012年10月21日














