立方八面体 [ 3,4,3,4 ] Cuboctahedron
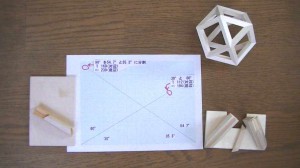
“三角の組み物” と兄弟関係にある立方八面体の 製作関連写真です。
この多面体は 製作2 製作3 でお伝えした 二十・十二面体と同じく
一つの形状の部品で組み立てられ 三角形に組んだ部品の結合でできます。
クレィドルも 傾斜は一つの角度 ( 30°)で
余角の 60°でカットした面を垂直にした部品を
二種類の接合角 (54.7°と35.3°計 90°) になるよう整形し
部品の両端の形状を 二十・十二面体と同じく面対称にして 24個が必要です。
“三角の組み物”と立方八面体が 兄弟関係にあると説明しましたが
組み物や多面体の頂点の位置が 合同になることができ
組み物の部品の太さと長さの比の値を この立方八面体から計算できるからです。
計算方法は説明困難ですが
多面体の三角形の面と中芯点とでできる立体は “正四面体” で
組み物の外周線は正四面体の面に斜めに “接して” います。
これらを条件として計算をしています。
私は 立方八面体を [ 3,4,3,4 ] (さんよん さんよん)と 呼んでいます。
多面体の一つの頂 (ちょう) に集まる多角形の状態を表しています。
形状が判り すっきりしている気がします。
複数の正多角形でできている準正多面体 の名称は
形状を確定するプロセスや いきさつが解かっていないと
意味不明な部分が多く 馴染みにくい気がします。
正四面体は [ 3,3,3 ](さんみっつ) 正六面体は [ 4,4,4 ] (よんみっつ)。
正八面体は [ 3,3,3,3 ] (さんよっつ)正十二面体は [ 5,5,5 ] (ご みっつ)。
正二十面体は [ 3,3,3,3,3 ] (さんいつつ)とも表現できます。
これらはどれも 正多角形が一種類でできていて 正多面体と呼ばれています。
今までにお伝えした 複数の正多角形でてきた準正多面体 は以下です。
二十・十二面体は [ 3,5,3,5 ]
サッカーボールは [ 5,6,6 ]で 切頂二十面体や
フラーレン fullerene とも呼ばれています。
2012年7月2日

