13[3,3,3,3,5]

外接球半径 2

04[3,3,3,3,3] 07[3,3,3,3,4] 13[3,3,3,3,5] Excel 多面体 諸量

かなり オタクな 計算遊びのつづきです。

前回 [ 3,3,3,3,5 ] の 外接球半径の計算式を Wolfram Alpha 計算知能で 求めました。
今回 その入力の値を (PI/2-PI/5) から (PI/2-PI/4) に変え
[ 3,3,3,3,4 ] の 値として

(ASIN(1/2/(1-0.5^2/X^2)^(1/2)))*8+(ASIN(SIN((PI/2-PI/4))*2/2/(1-0.5^2/X^2)^(1/2)))*2=2*PI
と 入力し Wolfram Alpha →　
計算式が表示されました。

Excel や Wolfram の入力用に 変換した式は以下です。

1/(4*SQRT(6/(80+(101888-1536*SQRT(33))^(1/3)+8*(199+3*SQRT(33))^(1/3))))
Wolfram Alpha →

私が 以前ご報告した 計算式は
SQRT(-(21/(2*(-22+(566-42*SQRT(33))^(1/3)+(566+42*SQRT(33))^(1/3))))) でした。

同様に [ 3,3,3,3,3 ] の 値として
その入力の値を (PI/2-PI/4) から (PI/2-PI/3) に変えるとか

すべて 三角形なので
ASIN(1/2/(1-0.5^2/X^2)^(1/2)))*2*5=2*PI にすると

1/2*SQRT(5/2+SQRT(5)/2) が返えってきました。
以前報告の 計算式は
1/2*SQRT(1/2*(5+SQRT(5)))　でした。

三種類それぞれ 計算式は異なっていても 計算数値は全てどれもイコールでした。

もう オタクな計算遊びは やめにして
次回のブログは ダイヤモンド結晶模型について載せようかと思っています。

2021年6月6日

外接球半径

13[3,3,3,3,5] Excel 多面体 諸量

かなり オタクな 計算遊びをひとつ。

以前 ラズパイ上で動作する Wolfram 製品の簡易なマセマティカ を用いて
[ 3,3,3,3,5 ] の 外接球半径の計算式を求めたのですが → Raspberry Pi で Mathematica
見つけられず あっさり断念した経緯がありました。

その後 インターネット上で 外接球半径が計算できる式を発見し　
その数式を利用させてもらい 現在に至っています。

しかし 前回のブログをきっかけに 考えなおしていると

X の解を求める 二分法の計算式を用いて Wolfram Alpha 計算知能　という
検索できる (https://www.wolframalpha.com/)
フリーの数理処理システムで X の解を得ることができました。

Wolfram の マセマティカ と同じ ロジックで 処理がなされています。

(ASIN(1/2/(1-0.5^2/X^2)^(1/2)))*8+(ASIN(SIN((PI/2-PI/5))*2/2/(1-0.5^2/X^2)^(1/2)))*2=2*PI
と 入力し Wolfram Alpha →
計算式が表示されました。
Excel や Wolfram の入力用に 変換した式は以下です。

SQRT(9/8+7*SQRT(5)/24+1/384*(83755008+37437440*SQRT(5)-16384*SQRT(64233+28728*SQRT(5)))^(1/3)+1/12*(1/2*(5112+2285*SQRT(5)+SQRT(64233+28728*SQRT(5))))^(1/3))
Wolfram Alpha →

2021年6月4日

パズル気分 で 外接球半径 再掲

13[3,3,3,3,5] Excel 多面体 諸量

諸量計算について 幾度かお伝えしていますが
その中で Excel で作った 外接球半径計算の リメイク版を載せておきます。

このワークシートでは 二分法 という計算手法を用いて
プラトン多面体やアルキメデス多面体の 外接球半径すべてが計算できます。

この 二分法という計算方法を使えたことにより
[ 3,3,3,3,4 ] や [ 3,3,3,3,5 ] の外接球半径の計算値が 他資料の参照ではなく
自前で求めることができました。
計算結果が参考資料と合致しており とても嬉しく思ったことを記憶しています。

 面が五つある [3,3,3,3,3] [3,3,3,3,4] [3,3,3,3,5] 以外は 以前お伝えしている
 ブラーマグプタの公式 ( Brahmagupta’s formula ) で すべて求められます。
以下がその二分法で解く Excel データです。
転記方法は text として A列 1行目‎に 全範囲を copy and paste してください。
C列の 12行目から C列の 26行目までが入力欄です。
H列の 12行目から H列の 26行目までが その解答数値です。

30行目以下のデータは 計算初期データで
02行目のデータは
42行目データを copy and paste したものです。


     a b c d e基本数別解 


 13 [3,3,3,3,5]  3 3 3 3 5 =SQRT(I2^2-0.5^2)/I2  =1/12*SQRT(6*(27+7*SQRT(5)+(20448+9140*SQRT(5)-12*SQRT(7137+3192*SQRT(5)))^(1/3)+(20448+9140*SQRT(5)+12*SQRT(7137+3192*SQRT(5)))^(1/3))) 


           


  多角形 角数 開き寸 かど心寸 開き角 頂芯寸    


  a =C2 =SIN((PI()/2-PI()/C5))*2 =$D$27 =DEGREES(ASIN(D5/2/E5))*2 = IF(F10=360, 1/2/SQRT(1-D27^2),"")    


  b =D2 =SIN((PI()/2-PI()/C6))*2 =$D$27 =DEGREES(ASIN(D6/2/E6))*2    


  c =E2 =SIN((PI()/2-PI()/C7))*2 =$D$27 =DEGREES(ASIN(D7/2/E7))*2    


  d =F2 =IF(C8=0,0,SIN((PI()/2-PI()/C8))*2) =$D$27 =DEGREES(ASIN(D8/2/E8))*2    


  e =G2 =IF(C9=0,0,SIN((PI()/2-PI()/C9))*2) =$D$27 =DEGREES(ASIN(D9/2/E9))*2     


      =SUM(F5:F9)     


  桁 入力     =ASC(H2)&"0"    


  1 9 =(1/10)^B12*C12    =VALUE(MID($H$11,B12+2,1))   


  2 7 =(1/10)^B13*C13    =VALUE(MID($H$11,B13+2,1))   


  3 2 =(1/10)^B14*C14    =VALUE(MID($H$11,B14+2,1))   


  4 7 =(1/10)^B15*C15    =VALUE(MID($H$11,B15+2,1))   


  5 3 =(1/10)^B16*C16    =VALUE(MID($H$11,B16+2,1))    


  6 2 =(1/10)^B17*C17    =VALUE(MID($H$11,B17+2,1))   


  7 8 =(1/10)^B18*C18    =VALUE(MID($H$11,B18+2,1))    


  8 5 =(1/10)^B19*C19    =VALUE(MID($H$11,B19+2,1))   


  9 0 =(1/10)^B20*C20    =VALUE(MID($H$11,B20+2,1))   


  10 5 =(1/10)^B21*C21    =VALUE(MID($H$11,B21+2,1))    


  11 6 =(1/10)^B22*C22    =VALUE(MID($H$11,B22+2,1))   


  12 5 =(1/10)^B23*C23    =VALUE(MID($H$11,B23+2,1))    


  13 5 =(1/10)^B24*C24    =VALUE(MID($H$11,B24+2,1))    


  14 9 =(1/10)^B25*C25    =VALUE(MID($H$11,B25+2,1))   


  15 6 =(1/10)^B26*C26    =VALUE(MID($H$11,B26+2,1))    


    =SUM(D12:D26)        


          


   a b c d e    


 01 [3,3,3]  3 3 3   =SQRT(I30^2-0.5^2)/I30  =SQRT(3/2)/2 


 02 [3,3,3,3]  3 3 3 3  =SQRT(I31^2-0.5^2)/I31  =1/SQRT(2) 


 03 [4,4,4]  4 4 4   =SQRT(I32^2-0.5^2)/I32  =SQRT(3)/2 


 04 [3,3,3,3,3]  3 3 3 3 3 =SQRT(I33^2-0.5^2)/I33  =1/2*SQRT(1/2*(5+SQRT(5))) 


 05 [3,4,3,4]  3 4 3 4   =SQRT(I34^2-0.5^2)/I34  =1 


 06 [3,6,6]  3 6 6   =SQRT(I35^2-0.5^2)/I35  =SQRT(11/2)/2 


 07 [3,3,3,3,4]  3 3 3 3 4 =SQRT(I36^2-0.5^2)/I36  =SQRT(-(21/(2*(-22+(566-42*SQRT(33))^(1/3)+(566+42*SQRT(33))^(1/3))))) 


 08 [3,4,4,4]  3 4 4 4  =SQRT(I37^2-0.5^2)/I37  =1/SQRT(4-2/COS(1/2*ACOS(1/4*(2-SQRT(2))))^2) 


 09 [5,5,5]  5 5 5   =SQRT(I38^2-0.5^2)/I38  =1/2*SQRT(3/2*(3+SQRT(5))) 


 10 [4,6,6]  4 6 6   =SQRT(I39^2-0.5^2)/I39  =SQRT(5/2) 


 11 [3,5,3,5]  3 5 3 5  =SQRT(I40^2-0.5^2)/I40  =SQRT(1/2*(3+SQRT(5))) 


 12 [3,8,8]  3 8 8   =SQRT(I41^2-0.5^2)/I41  =1/2*SQRT(7+4*SQRT(2)) 


 13 [3,3,3,3,5]  3 3 3 3 5 =SQRT(I42^2-0.5^2)/I42  =1/12*SQRT(6*(27+7*SQRT(5)+(20448+9140*SQRT(5)-12*SQRT(7137+3192*SQRT(5)))^(1/3)+(20448+9140*SQRT(5)+12*SQRT(7137+3192*SQRT(5)))^(1/3))) 


 14 [3,4,5,4]  3 4 5 4  =SQRT(I43^2-0.5^2)/I43  =1/4*(-1+SQRT(5))*SQRT(1/2*(53+23*SQRT(5))) 


 15 [4,6,8]  4 6 8   =SQRT(I44^2-0.5^2)/I44  =1/2*SQRT(13+6*SQRT(2)) 


 16 [5,6,6]  5 6 6   =SQRT(I45^2-0.5^2)/I45  =1/2*SQRT(1/2*(29+9*SQRT(5))) 


 17 [3,10,10]  3 10 10   =SQRT(I46^2-0.5^2)/I46  =1/2*SQRT(1/2*(37+15*SQRT(5))) 


 18 [4,6,10]  4 6 10   =SQRT(I47^2-0.5^2)/I47  =1/2*SQRT(31+12*SQRT(5))
　

2021年5月30日

ディスプレイのことも少しは

11[3,5,3,5] 13[3,3,3,3,5] 多面体


コロナヴァイラスに 翻弄される毎日です。

多面体を作っても ディスプレイに関してほとんど お伝えしていませんでした。

映像左は 100円で買った できあいですが モイチ納得できません。


その右は 七角形のフレィムで作った吊るし台です。
竹の四角棒 5×5×100 を左右 64.29°(297/143) でカットし
木工用ボンドで接着しています。

上から吊らさず
横の辺の部分から てぐすで保持しています。
精度よく加工すれば 強度は保てています。
そのフレィムを 90° と 128.6°の かぎ状にそれぞれ接着した
5×10×70 の板棒四本で挟んでいます。

64.29°(297/143) の計算手順は。
360 / 7 = 51.429
180 – 51.429 = 128.57
128.57 / 2 = 64.286
64.286 のタンジェントは 2.0765 / 1
297 / 2.0765 = 約 143
2.0765 / 1 = 約 297 / 143 になります。

2021年5月16日

パズル気分 で 外接球半径

13[3,3,3,3,5] Excel 多面体 諸量

ブラーマグプタの公式 ( Brahmagupta’s formula ) で 外接球半径 ( 頂芯寸 )
を Excel で解く計算式を前回 お伝えしました。

このブログで扱っている多面体は
プラトン多面体と アルキメデス多面体 を主な対象にしていますが
面が五つある [3,3,3,3,3] [3,3,3,3,4] [3,3,3,3,5] は無理でした。

今回は 未知数を 二分法を使って Excel で解く計算式を載せておきます。
パズル気分で 求められるとして 既に掲載している計算方法の 改良版です。

色付けした全範囲を指定し 1 行目 A 列に copy and paste してください。
貼り付けのオプションは
貼り付け先の書式に合わせる(M)です。
でないと バックの ブルーの色まで 表示してしまいます。

30 行目から 47 行目まで はデータです。
データを 2 行目 に copy and paste してください。

C 列 の 12 行から 26 行 に数字を入力してください。
13[3,3,3,3,5] の回答がサンプルとして入っています。

H 列 の 12 行から 26 行 に 答えが表示されています。
H 列 の 巾を 0 にするか
セルの書式設定で H 列 のフォントの色(C)を 白 にしてください。

そして F 列 の 5 行 から G 列 の 10 行 までの範囲を指定し
セルの書式設定で 分類を 数値にし
小数点以下の桁数を 15 にしてください。

遊び方は
最初 C 列の入力欄 2桁目から 15桁めまでを 0 にします。
0 から 9 までの数字を 1 桁目に入れて　　　　　　　＊注
開き角の計が 360 より大で
その差が 最少になったら
次の桁に進み 同じようにして続けます。
サンプルの画面で 練習するとコツがわかります。



     a b c d e   


 13 [3,3,3,3,5]  3 3 3 3 5 0.972732850565596  


          


  多角形 角数 開き寸 かど心寸 開き角 頂芯寸   


  a =C2 =SIN((PI()/2-PI()/C5))*2 =$D$27 =DEGREES(ASIN(D5/2/E5))*2 = IF(F10=360, 1/2/SQRT(1-D27^2),"")   


  b =D2 =SIN((PI()/2-PI()/C6))*2 =$D$27 =DEGREES(ASIN(D6/2/E6))*2    


  c =E2 =SIN((PI()/2-PI()/C7))*2 =$D$27 =DEGREES(ASIN(D7/2/E7))*2    


  d =F2 =IF(C8=0,0,   SIN((PI()/2-PI()/C8))*2) =$D$27 =DEGREES(ASIN(D8/2/E8))*2    


  e =G2 =IF(C9=0,0,   SIN((PI()/2-PI()/C9))*2) =$D$27 =DEGREES(ASIN(D9/2/E9))*2    


      =SUM(F5:F9)    


  桁 入力     =ASC(H2)&"0"  


  1 9 =(1/10)^B12*C12    =VALUE(MID($H$11,B12+2,1))  


  2 7 =(1/10)^B13*C13    =VALUE(MID($H$11,B13+2,1))  


  3 2 =(1/10)^B14*C14    =VALUE(MID($H$11,B14+2,1))  


  4 7 =(1/10)^B15*C15    =VALUE(MID($H$11,B15+2,1))  


  5 3 =(1/10)^B16*C16    =VALUE(MID($H$11,B16+2,1))  


  6 2 =(1/10)^B17*C17    =VALUE(MID($H$11,B17+2,1))  


  7 8 =(1/10)^B18*C18    =VALUE(MID($H$11,B18+2,1))  


  8 5 =(1/10)^B19*C19    =VALUE(MID($H$11,B19+2,1))  


  9 0 =(1/10)^B20*C20    =VALUE(MID($H$11,B20+2,1))  


  10 5 =(1/10)^B21*C21    =VALUE(MID($H$11,B21+2,1))  


  11 6 =(1/10)^B22*C22    =VALUE(MID($H$11,B22+2,1))  


  12 5 =(1/10)^B23*C23    =VALUE(MID($H$11,B23+2,1))  


  13 5 =(1/10)^B24*C24    =VALUE(MID($H$11,B24+2,1))  


  14 9 =(1/10)^B25*C25    =VALUE(MID($H$11,B25+2,1))  


  15 6 =(1/10)^B26*C26    =VALUE(MID($H$11,B26+2,1))  


    =SUM(D12:D26)      


          


   a b c d e   


 01 [3,3,3]  3 3 3   0.577350269189626  


 02 [3,3,3,3]  3 3 3 3  0.707106781186548  


 03 [4,4,4]  4 4 4   0.816496580927726  


 04 [3,3,3,3,3]  3 3 3 3 3 0.85065080835204  


 05 [3,4,3,4]  3 4 3 4  0.866025403784439  


 06 [3,6,6]  3 6 6   0.904534033733291  


 07 [3,3,3,3,4]  3 3 3 3 4 0.928191377985572  


 08 [3,4,4,4]  3 4 4 4  0.933948831094465  


 09 [5,5,5]  5 5 5   0.934172358962716  


 10 [4,6,6]  4 6 6   0.948683298050514  


 11 [3,5,3,5]  3 5 3 5  0.951056516295154  


 12 [3,8,8]  3 8 8   0.959682982260667  


 13 [3,3,3,3,5]  3 3 3 3 5 0.972732850565596  


 14 [3,4,5,4]  3 4 5 4  0.97460776237817  


 15 [4,6,8]  4 6 8   0.976450976246513  


 16 [5,6,6]  5 6 6   0.979432085486414  


 17 [3,10,10]  3 10 10   0.985721919281302  


 18 [4,6,10]  4 6 10   0.991316689541059
＊注
1 から 9 までの数字を と 表示していました
0 から 9 までの数字を が 正しいです。
すみませんでした、二桁目からは 0 もあり得ます。
お詫びし 訂正いたします。
　　　　　　　　　　　　　　　　　　　　　　　　　　2016 12月06日

2016年11月9日

[3,3,3,3,5] の計算式

13[3,3,3,3,5] Excel 多面体 未分類 諸量

前々回と前回の続きです。

また [3,3,3,3,5] の 外接球半径についてです。

計算式が判明していないのが残念です。と書いていました。

しかし
日本語版の Wikipedia の変形十二面体に 計算式が載っていました。
(2015年3月16日 (月) 07:24時点における版 より)

他の言語での Wikipedia では 載っていないようです。

灯台もと暗しです。

自力解決のため
他の人の成果をあまり 参考にしなかったと 言い訳けを言っておきます。

エクセルで 計算できる表現で記述すると 以下です。

=1/12*SQRT(6*(27+7*SQRT(5)+
(20448+9140*SQRT(5)-12*SQRT(7137+3192*SQRT(5)))^(1/3)+
(20448+9140*SQRT(5)+12*SQRT(7137+3192*SQRT(5)))^(1/3)))

実行すると 2.15583737511564　の値になりました。

Mathematica や 多倍長電卓LM でその計算式を実行すると
以下の値になりました。　　1000桁指定で。
 2.15583 73751 15639 70183 66290 76693 05827 70168 51218 77481
   18224 12215 43012 00670 80949 48400 05342 99263 65092 81214
   42837 81342 43246 21737 40459 54065 85302 63076 41156 48362
   61553 40520 55788 21730 48597 74900 41955 04806 67994 23712
   71525 28776 34895 69926 86212 88569 85191 74933 10255 37663
   89383 63399 79283 76418 99149 18774 71118 22568 83717 98931
   40550 29409 01766 94946 34398 87848 02244 57311 06529 13448
   70006 06489 44983 26040 49885 95916 78242 35322 86706 43588
   24725 85106 61761 48622 26035 08409 42037 97200 85433 87619
   26185 48385 92161 45979 67530 77814 04162 76223 45964 17424
   61662 74884 37069 41777 65349 61375 79611 76459 55281 47239
   10055 92400 99532 46993 91697 07642 18254 78816 20917 41323
   30782 90598 28269 61852 86046 33222 90369 70537 94291 22137
   57735 96999 29115 55796 89248 85516 55653 42479 66607 96000
   32588 71439 21773 89617 00919 44329 45587 06989 26937 50828
   21538 82298 47919 43690 77468 78574 65464 48587 09674 43132
   37827 12811 11579 23998 93711 92216 62371 10941 63488 80174
   32408 80103 95417 13989 24604 02990 42663 64012 26025 37471
   22022 18750 24148 80322 37766 49193 81488 04859 20840 56198
   29812 04572 02410 92578 25763 62541 58115 04268 63472 9041
Mathematica　での計算内容を確認できます。⇒ Wolfram Alpha

2016年9月3日

[3,3,3,3,4] と [ 3,3,3,3,5] の外接球半径 1000桁

07[3,3,3,3,4] 13[3,3,3,3,5] Excel 多面体 未分類 諸量

前回の続きです。

Raspberry Pi で Mathematica　を走らせて
多面体の 外接球半径 ( 頂芯寸 ) のシンプルな計算式を求めたとして
Excel で使用できる 表を載せました。

計算式という 式にこだわっているのは
その式の表現する値は 近似値ではないからです。

Excel で [3,3,3,3,4] の 頂芯寸の 計算式は
=SQRT(-(21/(2*(-22+(566-42*SQRT(33))^(1/3)+(566+42*SQRT(33))^(1/3))))) で
表示は 15桁の表示指定で 1.343713373744600 となっています。

この数式を 多倍長電卓LM で１０００桁指定で 実行すると以下です。

[3,3,3,3,4] 外接球半径

 1.34371 33737 44601 70127 15287 53975 05824 76376 02609 35358
   64988 77762 09658 55706 90893 48794 56973 31688 73082 16628
   10517 86312 34231 18912 48934 22698 98513 13152 52388 83099
   99695 51465 34656 54666 91199 73057 12404 87181 58689 83101
   52706 73588 95439 45759 66808 98001 82458 74562 03715 47798
   73758 91138 64065 13093 44833 73642 76320 04740 38209 97931
   21283 63087 45536 25488 82847 16710 31601 12312 74946 88760
   75947 23068 26438 72263 54595 16709 53642 47794 39632 74759
   99864 48261 56826 97693 61084 82504 65047 47725 73973 75581
   77519 56125 26881 51031 78761 94824 75418 84415 24688 37953
   07401 46214 60745 49416 60020 61203 67766 70368 45208 15639
   13255 40719 84840 73695 37115 68354 45051 94655 39154 15438
   52061 97480 37458 38311 41863 43914 37952 62153 58312 90302
   21901 83004 41970 32795 85375 45937 91929 07117 32102 04879
   62563 41502 88258 97563 31599 80542 81380 61709 57750 80055
   92392 17968 33724 70868 62099 96630 67075 59371 76770 36409
   06359 45200 09505 63444 91600 53436 55518 90992 23660 99813
   72421 11438 19374 00218 74596 54930 76261 02604 25038 80259
   06749 56526 92077 83952 39016 51486 43263 70810 40971 32169
   84435 10226 61936 74850 55855 77017 66200 17485 66370 5204
以前掲載した 諸量の計算プログラム では 1.34371337374461 でした。

このプログラムと同じ ロジックで 多倍長電卓に 計算させた値と
上の 1000桁の値とは イコールでした。

同じように [3,3,3,3,5] を計算させると 以下になりました。
1000桁の精度は 維持できていると思います。
計算式が判明していないのが残念です。
[3,3,3,3,5] 外接球半径

 2.15583 73751 15639 70183 66290 76693 05827 70168 51218 77481
   18224 12215 43012 00670 80949 48400 05342 99263 65092 81214
   42837 81342 43246 21737 40459 54065 85302 63076 41156 48362
   61553 40520 55788 21730 48597 74900 41955 04806 67994 23712
   71525 28776 34895 69926 86212 88569 85191 74933 10255 37663
   89383 63399 79283 76418 99149 18774 71118 22568 83717 98931
   40550 29409 01766 94946 34398 87848 02244 57311 06529 13448
   70006 06489 44983 26040 49885 95916 78242 35322 86706 43588
   24725 85106 61761 48622 26035 08409 42037 97200 85433 87619
   26185 48385 92161 45979 67530 77814 04162 76223 45964 17424
   61662 74884 37069 41777 65349 61375 79611 76459 55281 47239
   10055 92400 99532 46993 91697 07642 18254 78816 20917 41323
   30782 90598 28269 61852 86046 33222 90369 70537 94291 22137
   57735 96999 29115 55796 89248 85516 55653 42479 66607 96000
   32588 71439 21773 89617 00919 44329 45587 06989 26937 50828
   21538 82298 47919 43690 77468 78574 65464 48587 09674 43132
   37827 12811 11579 23998 93711 92216 62371 10941 63488 80174
   32408 80103 95417 13989 24604 02990 42663 64012 26025 37471
   22022 18750 24148 80322 37766 49193 81488 04859 20840 56198
   29812 04572 02410 92578 25763 62541 58115 04268 63472 9041

2016年9月1日

sashimono[3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 5

13[3,3,3,3,5] Carbon nanotube 多面体



Ｓ形の結合部品の組合せ作業のみで迷うことなく簡単に
Pentagonal Hexecontahedron が完成しました。

簡単にとは言っても 稜部品のカットと整形には 飽きるほど単純な反復作業に耐えてきましたが。

次に何をしようかと迷っています。
今までの製作方法の説明と 諸量のデータで 正多面体 準正多面体 双対多面体 そしてそれらの複合多面体 compounds はつくれるはずです。
しかし 私の説明がうまく伝えられていればのことですが。

私自身まだ 作っていない多面体や 複合多面体がありますので
思いつくまま製作して それをお伝えしようかなと 今思っています。

一番最初のブログで お伝えするとしてまだ実行していないものがあります。
それはカーボンナノチューブ (Carbon nanotube) 模型です。
平面充填六角形の円柱座標での取り扱いという単純な作業ではなく。
平面充填三角形のかど点を 三次元の中の円柱面に投影するという説明が必要です。
またその中のタイプの spiral な形状の説明も必要となってきます。
私には大変 困難なことです。少しずつ 準備をしてゆこうと思っています。
球ではなく円柱を取り扱うため symmetry なことではかなり劣りますし。
sashimono としては歪みが生じます。
どれだけ関心のある方たちが居られるかも不安ではあります。

2012年10月21日

sashimono[3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 4

13[3,3,3,3,5] 多面体 製作道具



[3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 製作途中です。

左上の四角形の板で作った部品で 三角形の面の上にくる稜の部品をカットします。
その右下の四角形の板で 五角形の面の上にくる稜の部品をカットします。
左端中ほどの 角度の鋭い加工部分のある cradle で五角形の面の上にくる稜部品を整形します。 19.158度の仰角があります。
そしてもう片方の鈍角な加工部分のある cradle で三角形の面の上にくる稜部品を整形します。 7.912度の仰角があります。
寸法の長い 三角形面と五角形面とをまたぐ稜部品はこの二つの cradle をつかいます。
寸法の短い 三角形面と三角形面とをまたぐ稜部品は鈍角な加工部分のある cradle のみをつかいます。

部品は二種類　(3,3形　3,5形)　です。
部品を縦方向に置いた場合 以下の形状と個数でず。
三角形をつくる接合面が左右 上下ともにあるもの (3,3形) が 90個必要です。
上下どちらか一端の 左右が 三角形を そしてその反対側の 左右が五角形をつくるもの (3,5形) が 60個必要です。

この[3,3,3,3,5] 双対多面体も鏡像体が存在し 接合作業で混乱が生じる場合があります。
それを回避するための一つの方法が以下です。

元の[3,3,3,3,5] 多面体と同じように 基本的な結合部品があります。
形状が鏡像関係にある結合部品 (Ｎ形 Ｓ形) があり どちらか一方の部品の集合で多面体が完成します。
画面中ほど上に 小さい部品 (3,3形) 三つでＮのような形に接合しそれに長い部品 (3,5形) を二つ結合させた結合部品が Ｎ形 です。
画面中央に 小さい部品 (3,3形) 三つでＳのような形に接合しそれに長い部品 (3,5形) を二つ結合させた結合部品 (Ｓ形) があります。
今回は Ｓ形の結合部品の組合せで作業を進めてゆこうとしています。

2012年10月19日

sashimono[3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 3

13[3,3,3,3,5] 多面体 製作道具



[3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 製作に必要なもの についてお伝えします。
左のグラフ用紙の上方向にある 三角形の部品は 元の多面体 (変形12面体 Snub Dodecahedron) の 5角形の上にくる稜の仰角をつくる傾斜部品です。その角度は 底辺 213 対辺 074 で表される 斜線をプロットして得られます。
その線に沿って置いてある四角形の板が 90度から仰角を引いた角度 (余角)で稜部品をカットするものです。
10×10 の角材の断面の対角線方向にカットした形状のものを二本貼っています。

左下方向にある 三角形の部品は 元の多面体 (変形12面体 Snub Dodecahedron) の 3角形の上にくる稜の仰角をつくる傾斜部品です。
底辺 223 対辺 031 で表される 斜線をプロットして得られます。
四角形の板はその余角で稜部品をカットするものです。

右のグラフ用紙は [3,3,3,3,5] 双対多面体の稜寸を求めるものです。
二本の勾配を比較して 90度に近い方が 3角形と3角形とをまたぐ稜寸を決めるものです。
双対多面体の面から双対多面体の中芯点までの距離 (面芯寸)を 1としたとき
稜の寸法は 0.2858 になり 対辺 070 底辺 245 でグラフ用紙にその比が得られます。
二つ目の勾配の線が5角形と3角形とをまたぐ稜寸 / 面芯寸 ( 125/250 ) です。
グラフ用紙に載っている二つの部品は 面芯寸が 100mmのときの　稜の部品の寸法になっています。

2012年10月18日

sashimono[3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 2

13[3,3,3,3,5] 多面体 製作道具



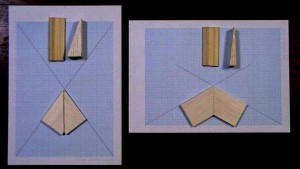
[3,3,3,3,5] 双対多面体の クレィドル cradle の製作中です。

左側のグラフ用紙の上に乗った部品の説明をします。
元の多面体 (変形12面体 Snub Dodecahedron) の
5角形の上にくる稜をつくる cradle です。

接合角は 72度で 左右それぞれ 36度 (360/5/2度 178/245) になります。
その角度は 底辺 245 対辺 178 で表される 斜線を
左右対称にプロットして得られます。

その上方向にある 三角形の部品は
19.158度 (074/213) の仰角をつくる傾斜部品です。
その角度は 底辺 213 対辺 074 で表される 斜線をプロットして得られます。
厚さが 20mm のバルサ材です。

その横にあるのが 巾 30mm の薄板の上に部品を貼ったものです。
10×10 の角材の断面の対角線方向にカットした形状のものを二本貼っています。
対角線方向を下にしています。

右側のグラフ用紙の上に乗った部品の説明をします。

元の多面体 (変形12面体 Snub Dodecahedron) の
3角形の上にくる稜をつくる cradle です。
接合角は 120度で 左右それぞれ 60度 (360/3/2度 194/112) になります。

その角度は 底辺 112 対辺 194 で表される 斜線を
左右対称にプロットして得られます。

その上方向にある 三角形の部品は
7.912度 (031/223) の仰角をつくる傾斜部品です。

その角度は 底辺 223 対辺 031 で表される 斜線をプロットして得られます。

2012年10月17日

sashimono[3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 1

13[3,3,3,3,5] 多面体



上は[3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 五角60面体です。

これからつくる製作説明の多面体は 10×10 のバルサ材で
直径20cm の大きさにしようと思っています。

正多面体や準正多面体 の稜寸や仰角は 1種類ですが
双対多面体の稜寸は ほとんど複数あります。
稜寸が1種類でも 仰角は複数あります。
[3,3,3,3,5] 双対多面体は
5角形と3角形の間の稜(3,5形)と 3角形と3角形の間の稜(3,3形) の二種類あります。

もとの多面体[3,3,3,3,5]を基準として以下に諸量の説明をします。
つまりもとの多面体の稜芯寸と こちらの稜芯寸とが同じ値としています。

面芯寸は 2.0399 です。

(3,5形)の稜寸は 1.0200 で 面芯寸との比は 125/250 です。
対辺 125 底辺 250 の比例関係をグラフにプロットしますと
対辺 100mm (作ろうとする多面体の半径) に対する 底辺の実寸は 約50mm になります。
つまり 直径 200mm の (3,5形)の稜寸は 約50mm です。
マザーになる部品の寸法を グラフから決定し それをコピーしながら部品を作ってゆきます。

(3,3形)の稜寸は 0.5829 で 面芯寸との比は 070/245 です。
直径 200mm の (3,3形)の稜寸は 約29mm です。

5角形の上にくる稜の仰角は 19.16度です。
グラフの上に 対辺74 底辺213 で表示できる角度です。
材料カットに必要な 仰角の余角 ( 90 – 19.16 ) もこれから求めます。

3角形の上にくる稜の仰角は 7.91度です。
グラフの上に 対辺31 底辺223 で表示できる角度です。

(3,5形)の稜の必要個数は 60で (3,3形)の稜の必要個数は 90です。

5角形の上にくる稜の接合角は 360 / 5 で 072度なので それぞれ片方が 36度になります。
3角形の上にくる稜の接合角は 360 / 3 で 120度なので それぞれ片方が 60度になります。
今回から 文章の表現方法を変えています。
過去の文章にも 修正を施しました。
英語への自動翻訳を少し意識しています。
以前の多くの文章が自動翻訳では 理解困難だったかもしれません。

2012年10月10日

sashimono [3,3,3,3,5]　変形12面体　Snub Dodecahedron 3

13[3,3,3,3,5] 多面体



[3,3,3,3,5] の稜の部品加工が終了し 組み立て作業に入っています。

部品は二種類　(3,3形　3,5形)　で 部品を縦方向に置いた場合
三角形をつくる接合面が左右 上下ともにあるもの (3,3形) が 90個と
片側 上下が 三角形を そして他の側の上下が五角形をつくるもの (3,5形) が 60個です。

この多面体には鏡像体が存在するため 接合作業で混乱が生じる場合があります。
これを避けるために 今回は一つの方法をとっています。

画面左下のほうに三つの部品 (3,3形) を S状につなげて 二つの部品 (3,5形) を添えているのと
三つの部品 (3,3形) を N状につなげて 二つの部品 (3,5形) を添えているのがありますが
S形に 3,5形二つを結合して 三角形二個つなげた基本結合部品と
N形に 3,5形二つを結合して 三角形二個つなげた基本結合部品との
どちらか一方のみの組合せで多面体 [3,3,3,3,5] が完成します。

今回 N形のほうで結合を進めています。



完成しました。
次回は [3,3,3,3,5] 双対多面体 Pentagonal Hexecontahedron 五角60面体の
製作手順を お伝えします。

2012年10月9日

sashimono [3,3,3,3,5]　変形12面体　Snub Dodecahedron 2

13[3,3,3,3,5] 多面体 製作道具



[3,3,3,3,5]準正多面体 の 変形12面体 Snub Dodecahedron の製作部品をつくってゆきます。
作業盆上の四角形の寸法カット用治具は ストッパーもガイドも付けていません。
位置決めのしるしに合わせて ノコギリでカットしてゆくだけです。
作業に慣れや 理解が進めば治具をシンプルにしてゆきます。

10×10 のバルサ材で 14cm の大きさにしようと思っています。
接合面の角度整形をする前の 部品は 1種類で 150個必要です。

仰角 13.411度は グラフ用紙に 対辺 36 底辺 151 の斜線から求め
材料カットに必要な 仰角の余角 ( 90 – 13.411 ) もこれから求めます。

寸法は 三角形の面を底にしたときの高さを 14cm として計算しました。
面芯寸は 2.0771 なので 対辺 243 底辺 117 の比例関係をグラフにプロットし
対辺 70 に対する 底辺の 実寸がその寸法で 約 33.7mm です。

もくもくと ただひたすら カット作業を進めてゆきます。

[3,3,3,3,5] 双対多面体は 10×10 のバルサ材で 20cm の大きさの製作を予定しています。

2012年10月5日

sashimono [3,3,3,3,5]　変形12面体　Snub Dodecahedron とその双対

13[3,3,3,3,5] 多面体



今回から [3,3,3,3,5] の多面体とその双対についてお伝えします。
左が [3,3,3,3,5] 変形12面体 Snub Dodecahedron を 5×5の太さのすす竹で表現。
高さは約 70mmです。
右が その双対多面体で Pentagonal Hexecontahedron 五角60面体。
高さは約 105mmです。

どちらの多面体も 鏡面対称の立体が存在します。

多面体の諸量です。

13         変形12面体　Snub Dodecahedron
13　0.9727 [3,3,3,3,5]　基本数
13　13.411 [3,3,3,3,5]　稜の仰角　( 036/151 )
13　56.273 [3,3,3,3,5]　5角形の接合角　( 250/167 )
13　30.932 [3,3,3,3,5]　3角形の接合角　( 148/247 )
13　2.1558 [3,3,3,3,5]　稜寸を 1としたときの頂芯寸 ( 166/077 の比例関係 )
13　2.0971 [3,3,3,3,5]　稜寸を 1としたときの稜芯寸 ( 216/103 の比例関係 )
13　1.9809 [3,3,3,3,5]　稜寸を 1としたときの 5角形の面芯寸 ( 208/105 の比例関係 )
13　2.0771 [3,3,3,3,5]　稜寸を 1としたときの 3角形の面芯寸 ( 243/117 の比例関係 )
13　55.287 [3,3,3,3,5]　稜寸を 1としたときの面積
13　37.617 [3,3,3,3,5]　稜寸を 1としたときの体積
13　[3,3,3,3,5]　5角形と 3角形の間の稜の必要個数は 60
13　[3,3,3,3,5]　3角形と 3角形の間の稜の必要個数は 90

双対の諸量 ( もとの多面体の 稜芯寸と こちらの稜芯寸とが同じ値として)
13　        五角60面体 Pentagonal Hexecontahedron
13　2.0399　双対[3,3,3,3,5]　面芯寸
13　2.0971　双対[3,3,3,3,5]　稜芯寸
13　2.2200　双対[3,3,3,3,5]　5角形上の頂芯寸
13　2.1172　双対[3,3,3,3,5]　3角形上の頂芯寸
13　19.158　双対[3,3,3,3,5]　5角形上の稜の仰角　( 074/213 )
13　7.9123　双対[3,3,3,3,5]　3角形上の稜の仰角　( 031/223 )
13　36.000　双対[3,3,3,3,5]　5角形上の稜の接合角　( 180/5度 178/245 )
13　60.000　双対[3,3,3,3,5]　3角形上の稜の接合角　( 180/3度 194/112 )
13　1.0200　双対[3,3,3,3,5]　5角形と3角形とをまたぐ稜寸
13　0.5829　双対[3,3,3,3,5]　3角形と3角形とをまたぐ稜寸
13　0.5000　双対[3,3,3,3,5]　5角形と3角形とをまたぐ稜寸 / 面芯寸 ( 125/250 )
13　0.2858　双対[3,3,3,3,5]　3角形と3角形とをまたぐ稜寸 / 面芯寸 ( 070/245 )
13　55.281　双対[3,3,3,3,5]　面積
13　37.588　双対[3,3,3,3,5]　体積
13　双対[3,3,3,3,5]　5角形と 3角形の間の稜の必要個数は 60
13　双対[3,3,3,3,5]　3角形と 3角形の間の稜の必要個数は 90

[3,3,3,3,5] の多面体とその双対多面体は 私の最も気に入っている立体の中に含まれます。

2012年10月4日