Compounds
08[3,4,4,4] Compounds 多面体 製作道具

[3,4,4,4] の compounds 複合多面体の cradle と 稜部品です。
5×5 のすす竹で 12cm の大きさで作ろうとしています。
左二つの cradle が 準正多面体 Rhombicuboctahedron
斜方立方8面体の稜部品製作用です。
4,3形と 4,4形の稜部品があり
4,3形とは 4角形の面と3角形の面に挟まれた 稜部品のことで
4,4形とは 4角形の面と4角形の面に挟まれた 稜部品のことです。
仰角は 20.94度 ( 075/196 ) で 稜部品の寸法は すべて 23.0mm になります。
左側二つのうちの 左の cradle が 4形の接合角 49.21度( 175/151 ) の加工をします。
この cradle で 稜線を挟んで左右とも 4形の形状の稜部品(4,4形)を 48個つくります。
左側二つのうちの 右の cradle が 3形の接合角 32.37度( 116/183 ) の加工をします。
この cradle で 片方が 3形の形状の稜部品をつくります。
そしてその片方を 上で説明した 4形の cradle で加工し (4,3形)として 24個つくります。
それと 4形と 3形が逆になっている稜部品を 24個つくります。
真ん中の cradle で 稜が直角に交差するための形状を作ります。
稜部品の すべての片端は 仰角 0度 接合各 45度×2 に加工します。
右二つの cradle が 双対多面体の Trapezoidal Icositetrahedron 凧形24面体製作用です。
4形と 3形の稜部品があり
4形とは 元の多面体 (Rhombicuboctahedron)の 4角形の面の上にくる 稜部品のことで
3形とは 元の多面体の 3角形の面の上にくる 稜部品のことです。
右側二つのうちの 左の cradle が 4形の接合角 45度( 180/180 ) の部品の加工をします。
仰角は 22.50度( 070/169 ) 寸法が 24.9mm で 72個つくります。
右側二つのうちの 右の cradle が 3形の接合角 60度( 194/112 ) の部品の加工をします。
仰角は 12.76度( 029/128 ) 寸法が 13.6mm で 24個つくります。
これらの cradle で 計 5種類の稜部品をつくることになります。
そして それらを組み合わせて 2種類の 十字状の結合部品をつくると 作業がうまくゆきます。
二種類とは
4角形と 4角形に挟まれた稜の中心を 4角形と 4角形をまたぐ稜が交差している結合部品と、
4角形と 3角形に挟まれた稜の中心を 4角形と 3角形をまたぐ稜が交差している結合部品。
2013年2月3日
08[3,4,4,4] Compounds 多面体
[3,4,4,4]の準正多面体と
その双対多面体を複合させた多面体についてお伝えします。
準正多面体 で作る 複合多面体 compounds の説明は
以前 [3,5,3,5] においても行っています。
二つの多面体の 稜芯寸は 同一の値として計算します。
つまり 二つの多面体の稜が 直角に交差する形になります。
全ての値は 準正多面体 の稜の寸法が 1 としたときの値です。
08 [3,4,4,4]compounds 複合多面体 作成に必要な諸量
08 .38268343236508977173 複[3,4,4,4]0.5 /稜芯寸( 075/196 )
08 .22654091966098642160 複[3,4,4,4]3形 稜寸/稜芯寸( 029/128 )
08 .41421356237309504880 複[3,4,4,4]4形 稜寸/稜芯寸( 070/169 )
08 20.941020472243838873 [3,4,4,4]仰角( 075/196 )
08 49.210529059074710890 [3,4,4,4]4形 接合角( 175/151 )
08 32.368412822775867329 [3,4,4,4]3形 接合角( 116/183 )
08 [3,4,4,4]4,4形稜部品 必要個数 48
08 [3,4,4,4]4,3形稜部品 必要個数 24
08 [3,4,4,4]4,3形と 鏡面対称 な稜部品 必要個数 24
08 22.500000000000000000 双[3,4,4,4]4形 仰角( 070/169 )
08 12.764389682754654315 双[3,4,4,4]3形 仰角( 029/128 )
08 45.000000000000000000 双[3,4,4,4]4形 接合角/2( 180/180 )
08 60.000000000000000000 双[3,4,4,4]3形 接合角/2( 194/112 )
08 双[3,4,4,4]4形稜部品 必要個数 72
08 双[3,4,4,4]3形稜部品 必要個数 24
2013年1月17日
11[3,5,3,5] Compounds 多面体

Icosidodecahedron 20・12面体 と Rhombic Triacontahedron 菱形30面体 との
複合多面体 compounds の製作途中です。

組み立て作業は終わりました。これから微調整をします。
高さは約 160mm 5×5 のすす竹です。
準正多面体 の複合多面体の製作は 今回が初めてでした。
しかし組み立て方法は簡単です。
Icosidodecahedron や Rhombic Triacontahedron を
作った経験があれば 説明するまでもないと思います。
始めにお伝えしました 十字架状の結合部品の組合せで完成します。
次回は [5,6,6] Truncated Icosahedron 切頂20面体 (サッカーボール)の
双対多面体 Pentakis Dodecahedron 五方12面体 についてお伝えしようと思っています。
2012年11月20日
11[3,5,3,5] Compounds 多面体 製作道具

[3,5,3,5]複合多面体 compounds の寸法の決定についてお伝えします。
[3,5,3,5]多面体と [3,5,3,5]双対多面体の稜芯寸を
同じ値にしなければなりません。
高さを約 160mm に予定をしていましたので、稜芯寸を 80mmとします。
それそれれの稜の寸法を得るために
稜寸と 稜芯寸の比を表わす直線を方眼紙に描きます。
[3,5,3,5]多面体の稜寸と稜芯寸の比は 1 対 1.5388 ( 154/237 ) ですが
稜の中間点で [3,5,3,5]双対多面体の稜と直角に交差するため
対辺 154 の 1/2 の 77 で 底辺 237 の斜線を引きます。
画面にある 3本の斜線の 真ん中の線がそれです。
3本の斜線の右側のが 対辺 125 底辺 250 で 5角形の中心の上にくる稜の比です。
3本の斜線の左側のが 対辺 034 底辺 178 で 3角形の中心の上にくる稜の比です。
縦方向に下から 80の座標の横線と斜線の交点からそれぞれの値が得られます。
この図では より正確な値を得るために 縦線 横線 斜線の必要部分を
カッターナイフで処理しています。実寸で 40.0mm 26.0mm 15.3mm となります。
左上の cradleで 平面に 45度+45度の角度ですべての稜部品の片側を整形します。
その下の ペアーの cradleで26.0mmの部品を 仰角 18度の傾斜で加工します。
左に接合角 58.28度 右に接合角 31.72度で 60個と、
右に接合角 58.28度 左に接合角 31.72度で 60個必要です。
右上の cradleで 40.0mmの部品を 26.57度の仰角で 60個加工します。
その下の cradleで 15.3mmの部品を 10.81度の仰角で 60個加工します。
これらの 4種類の形状部品で 画面にある十字架状の 結合部品を 60個つくります。
これを接着してゆけば 複合多面体が完成します。そのはずです。
この [3,5,3,5]複合多面体は 私にとって初めての製作です。
急いだり、作業に飽きたりして 品質の良くない部品を作らないよう、
ゆっくりと作ってゆこうと思っています。
11 1.5388 [3,5,3,5] 稜寸を 1としたときの稜芯寸 ( 237/154 )
11 .50000 双対[3,5,3,5] 5角形の中心の上にくる稜の寸法/稜芯寸 ( 125/250 )
11 .19098 双対[3,5,3,5] 3角形の中心の上にくる稜の寸法/稜芯寸 ( 034/178 )
2012年11月11日
11[3,5,3,5] Compounds 多面体 製作道具

[3,5,3,5]の複合多面体 compounds の製作に必要な治具です。
高さを約 160mm にして 5×5 のすす竹でつくる予定をしています。
今回は [3,5,3,5]多面体と[3,5,3,5]双対多面体の
稜の部材の形状加工についてです。
再びの説明となります。寸法の決定については 次回にお伝えします。
三枚あるA4の方眼紙の内の左の方眼紙の中に [3,5,3,5]多面体の治具があります。
方眼紙の左下かどから上方向 233 右方向 144の座標に線をひき、
そして 左上かどから下方向 233 右方向 144の座標に線をひき
58.28度を上下対称にプロットしています。
これが 5角形の接合角です。
この角度と90度との差(余角) が3角形の接合角(31.72度) になります。
つまり 5角形の接合角と 3角形の接合角を合計すると 丁度 90度です。
この方眼紙の右にある三角形ふたつの部材は15mmの厚みのバルサ材で、
対辺 077 底辺 237 でできる 仰角 18度の傾斜です。
これらの上にある 四角形の部材が
仰角18度の余角(72度)で切断面をつくり 寸法や形状を整える治具です。
そして cradleの傾斜の溝にする部材が 2セット写っています。
この多面体には 二種類のcradleが必要です。
左に接合角 58.28度 右に接合角 31.72度のcradleと、
右に接合角 58.28度 左に接合角 31.72度のcradleとです。
つづいて この方眼紙の右の二枚の方眼紙の説明をします。
この二つで [3,5,3,5]双対多面体のcradleを作ります。
二つの内の左側の図で
5角形の中心の上にくる稜を製作するためのcradleを作ります。
方眼紙の左下かどから 右方向 178 上方向 245の座標に線をひき、
そして左右対称に 右下かどから 左方向 178 上方向 245の座標に線をひき、
5角形の上の接合角 36.00度×2 をプロットしています。
傾斜の部材は 対辺 125 底辺 250 でできる 26.57度の仰角です。
二つの内の右側の図で
3角形の中心の上にくる稜を製作するためのcradleを作ります。
方眼紙の左下かどから上方向 194 右方向 112の座標に線をひき、
そして上下対称に 左上かどから下方向 194 右方向 112の座標に線をひき、
3角形の上の接合角 60.00度×2 をにプロットしています。
傾斜の部材は 対辺 034 底辺 178 でできる 10.81度の仰角です。
11 58.283 [3,5,3,5] 5角形の接合角 ( 233/144 )
11 31.717 [3,5,3,5] 3角形の接合角 ( 144/233 )
11 18.000 [3,5,3,5] 稜の仰角 ( 077/237 )
11 36.000 双対[3,5,3,5] 5角形の中心の上にくる稜の接合角/2 ( 360/5度/2 178/245 )
11 26.565 双対[3,5,3,5] 5角形の中心の上にくる稜の仰角 ( 125/250 )
11 60.000 双対[3,5,3,5] 3角形の中心の上にくる稜の接合角/2 ( 360/3度/2 194/112 )
11 10.812 双対[3,5,3,5] 3角形の中心の上にくる稜の仰角 ( 034/178 )
2012年11月9日
11[3,5,3,5] Compounds 多面体
[3,5,3,5]多面体と[3,5,3,5]双対多面体との諸量をもとに
複合多面体 compounds を作ってゆきます。
すでに諸量は お伝えしているのですが表示や説明が 稚拙だったと反省しています。
改めてお伝えします。
[3,5,3,5]の諸量です。
11 Icosidodecahedron 20・12面体
11 .95106 [3,5,3,5] 基本数
11 18.000 [3,5,3,5] 稜の仰角 ( 077/237 )
11 58.283 [3,5,3,5] 5角形の接合角 ( 233/144 )
11 31.717 [3,5,3,5] 3角形の接合角 ( 144/233 )
11 1.6180 [3,5,3,5] 稜寸を 1としたときの頂芯寸 ( 233/144 )
11 1.5388 [3,5,3,5] 稜寸を 1としたときの稜芯寸 ( 237/154 )
11 1.3764 [3,5,3,5] 稜寸を 1としたときの 5角形の面芯寸 ( 245/178 )
11 1.5115 [3,5,3,5] 稜寸を 1としたときの 3角形の面芯寸 ( 198/131 )
11 60 [3,5,3,5] 5角形と 3角形の間の稜の必要個数
11 29.305982844911989541 [3,5,3,5] 稜寸を 1としたときの面積
11 13.835525936249404140 [3,5,3,5] 稜寸を 1としたときの体積
[3,5,3,5]双対多面体 Rhombic Triacontahedron の諸量です。
寸法は もとの多面体 Icosidodecahedron の稜寸が 1のとき、
複合多面体となる寸法にしています。つまり 稜芯寸が同じです。
もとの多面体の 3角形や5角形の位置をもとに計算しています。
11 Rhombic Triacontahedron 菱形30面体
11 26.565 双対[3,5,3,5] 5角形の中心の上にくる稜の仰角 ( 125/250 )
11 10.812 双対[3,5,3,5] 3角形の中心の上にくる稜の仰角 ( 034/178 )
11 36.000 双対[3,5,3,5] 5角形の中心の上にくる稜の接合角/2 ( 360/5度/2 178/245 )
11 60.000 双対[3,5,3,5] 3角形の中心の上にくる稜の接合角/2 ( 360/3度/2 194/112 )
11 1.4635 双対[3,5,3,5] 面芯寸 ( 221/151 )
11 1.5388 双対[3,5,3,5] 稜芯寸 ( 237/154 )
11 .76942 双対[3,5,3,5] 5角形の中心の上にくる稜の寸法 ( 177/230 )
11 .29389 双対[3,5,3,5] 3角形の中心の上にくる稜の寸法 ( 072/245 )
11 .50000 双対[3,5,3,5] 5角形の中心の上にくる稜の寸法/稜芯寸 ( 125/250 )
11 .19098 双対[3,5,3,5] 3角形の中心の上にくる稜の寸法/稜芯寸 ( 034/178 )
11 1.0633 双対[3,5,3,5] 5角形と3角形をまたぐ稜の寸法 ( 168/158 )
11 .72654 双対[3,5,3,5] 5角形と3角形をまたぐ稜の寸法/面芯寸 ( 178/245 )
11 60 双対[3,5,3,5] 5角形と3角形をまたぐ稜の必要個数
11 30.338137289060528404 双対[3,5,3,5] 面積
11 14.800212429686842801 双対[3,5,3,5] 体積
2012年11月3日
06[3,6,6] Compounds 多面体
[3,6,6]の双対多面体 Triakis Tetrahedron 三方4面体 の製作についてお伝えします。
[3,6,6]双対多面体製作に必要な諸量です。
寸法は もとの多面体 Truncated Tetrahedron の稜寸が 1のとき、
複合多面体 compounds となる寸法にしています。つまり 稜芯寸が同じです。
06 .61237 [3,6,6] もとの多面体の稜寸を 1としたとき その 6角形の面芯寸
06 1.0206 [3,6,6] もとの多面体の稜寸を 1としたとき その 3角形の面芯寸
06 1.6330 [3,6,6] もとの多面体の稜寸を 1としたとき上の二つの値の合計。
つまり多面体[3,6,6]の高さ ( 178/109 の比例関係 )であり、これを "基準高" とします。
06 54.736 双対[3,6,6] もとの多面体の6角形の上の稜の仰角 ( 239/169 )
06 15.793 双対[3,6,6] もとの多面体の3角形の上の稜の仰角 ( 056/198 )
06 30.000 双対[3,6,6] もとの多面体の6角形の上の稜の接合角 ( 180/6度 112/194 )
06 60.000 双対[3,6,6] もとの多面体の3角形の上の稜の接合角 ( 180/3度 194/112 )
06 1.5000 双対[3,6,6] もとの多面体の6角形の上の稜寸
06 .30000 双対[3,6,6] もとの多面体の3角形の上の稜寸
06 1.8000 双対[3,6,6] もとの多面体の6角形と3角形をまたぐ稜寸
06 1.1023 双対[3,6,6] もとの多面体の6角形と3角形をまたぐ稜寸 / 基準高 ( 194/176 )
06 3.0000 双対[3,6,6] もとの多面体の6角形と6角形をまたぐ稜寸
06 1.8371 双対[3,6,6] もとの多面体の6角形と6角形をまたぐ稜寸 / 基準高 ( 248/135 )
06 17.909773867919159185 双対[3,6,6] 面積
06 5.7275649276110349476 双対[3,6,6] 体積
06 双対[3,6,6] もとの多面体の6角形と3角形をまたぐ稜の必要個数は 12
06 双対[3,6,6] もとの多面体の6角形と6角形をまたぐ稜の必要個数は 06
以下の値は複合多面体製作に必要な諸量です。
06 .30619 [3,6,6] もとの多面体の稜寸 / 基準高 / 2 ( 064/209 )
06 .91856 双対[3,6,6] もとの多面体の6角形の上の稜寸 / 基準高 ( 158/172 )
06 .18371 双対[3,6,6] もとの多面体の3角形の上の稜寸 / 基準高 ( 045/245 )
2012年10月28日
Compounds 多面体 諸量
双対多面体の諸量を掲載します。
寸法は もとの多面体の稜寸が 1のとき
複合多面体 compounds となる寸法にしています。
つまり 稜芯寸が同じです。
二面角 面芯寸 名称
70.528779365509308631 .20412414523193150818 01[3,3,3]
90.000000000000000000 .35355339059327376220 02[3,3,3,3]
109.47122063449069137 .57735026918962576451 03[4,4,4]
116.56505117707798935 .68819096023558676910 04[3,3,3,3,3]
120.00000000000000000 .75000000000000000000 05[3,4,3,4]
129.52119635864217322 .95940322360024695434 06[3,6,6]
136.30923289232420382 1.1576617909555498021 07[3,3,3,3,4]
138.11795905551232225 1.2202629537976100741 08[3,4,4,4]
138.18968510422140193 1.2228474935575285787 09[5,5,5]
143.13010235415597870 1.4230249470757706994 10[4,6,6]
144.00000000000000000 1.4635254915624211362 11[3,5,3,5]
147.35010012620952978 1.6382813268065143234 12[3,8,8]
153.17873255844969649 2.0398731549542789999 13[3,3,3,3,5]
154.12136312577632048 2.1209910195184334175 14[3,4,5,4]
155.08217961661841220 2.2097412102566332828 15[4,6,8]
156.71855372645878664 2.3771316059838161118 16[5,6,6]
160.61255220937037119 2.8852583129200411870 17[3,10,10]
164.88789190766248167 3.7366464560831424485 18[4,6,10]
L仰角 M仰角 S仰角
01 54.735610317245345685
02 35.264389682754654315
03 45.000000000000000000
04 20.905157447889299033
05 35.264389682754654315 19.471220634490691369
06 54.735610317245345685 15.793169048263962946
07 23.633863783205397467 13.382706143289984491
08 22.500000000000000000 12.764389682754654315
09 31.717474411461005324
10 35.264389682754654315 19.471220634490691369
11 26.565051177077989352 10.812316963571706291
12 45.000000000000000000 9.7356103172453456846
13 19.157762752181909888 7.9123169719830592329
14 18.434948822922010648 13.282525588538994676 7.6226318593503043571
15 32.235610317245345685 22.500000000000000000 12.764389682754654315
16 20.905157447889299033 16.472210692760396610
17 31.717474411461005324 5.6598937291886903186
18 24.094842552110700967 13.282525588538994676 7.6226318593503043571
L稜寸 M稜寸 S稜寸
01 .50000000000000000000
02 .35355339059327376220
03 .70710678118654752440
04 .30901699437494742410
05 .61237243569579452455 .30618621784789726227
06 1.5000000000000000000 .30000000000000000000
07 .54577648445886681200 .29673267798599365525
08 .54119610014619698440 .29598997565807943876
09 .80901699437494742410
10 1.0606601717798212866 .53033008588991064330
11 .76942088429381335064 .29389262614623656458
12 1.7071067811865475244 .29289321881345247560
13 .72853847965035469104 .29144976737249120721
14 .72541696649427383703 .51374314837300779674 .29124883602080337314
15 1.4270732708751722817 .93737914231134747753 .51266967637086882424
16 .92705098312484227231 .71764499555916901903
17 1.8090169943749474241 .29008936414773205235
18 1.6857166981731757817 .88982923502244570318 .50445778163332800082
Lかど角 Mかど角 Sかど角
01 60.000000000000000000
02 90.000000000000000000
03 60.000000000000000000
04 108.00000000000000000
05 70.528779365509308631 109.47122063449069137
06 33.557309761920715293 112.88538047615856941
07 80.751702088392428768 114.81207447790189281
08 81.578941881850578219 115.26317435444826534
09 60.000000000000000000
10 48.189685104221401934 83.620629791557196132
11 63.434948822922010648 116.56505117707798935
12 31.399714809919042210 117.20057038016191558
13 67.453508965514960111 118.13662275862125997
14 67.783011547435348796 86.974155491043547019 118.26867747047755717
15 37.773340083132792629 55.024696148902675288 87.201963767964532083
16 55.690639534406005565 68.618720931187988871
17 30.480324565355675308 119.03935086928864938
18 32.770278471287838669 58.237919620889530968 88.991801907822630362
L頂芯寸 M頂芯寸 S頂芯寸
01 .61237243569579452455
02 .61237243569579452455
03 1.0000000000000000000
04 .86602540378443864676
05 1.0606601717798212866 .91855865354369178682
06 1.8371173070873835736 1.1022703842524301442
07 1.3614101519264425345 1.2820358469890142117
08 1.4142135623730950488 1.3396704247226696103
09 1.5388417685876267013
10 1.8371173070873835736 1.5909902576697319299
11 1.7204774005889669228 1.5666546730064754191
12 2.4142135623730950488 1.7320508075688772935
13 2.2200006991613182111 2.1172098986276657420
14 2.2939698674519558970 2.2360679774997896964 2.1956534020612776371
15 2.6754174373368364913 2.4494897427831780982 2.3203772410170407352
16 2.5980762113533159403 2.5309268686270615215
17 3.4409548011779338455 2.9413907079821512843
18 4.1291457614135206146 3.8729833462074168852 3.8029832481815887597
面積 体積 LMS接合角
01 1.7320508075688772935 .11785113019775792073 60
02 3.0000000000000000000 .35355339059327376220 60
03 6.9282032302755091741 1.3333333333333333333 45
04 7.8859666817870040904 1.8090169943749474241 60
05 9.5459415460183915794 2.3864853865045978949 45 60
06 17.909773867919159185 5.7275649276110349476 30 60
07 19.299406563296038279 7.4473951888148613654 45 60
08 21.513454645857756671 8.7506905708484345088 45 60
09 22.672839422285121914 9.2418082864578952009 36
10 30.186917696247160902 14.318912319027587369 30 45
11 22.247967345311054163 10.853489115103684721 36 60 誤
11 30.338137289060528404 14.800212429686842801 36 60 正 2012 8/21
12 42.691767495934186821 23.313708498984760390 22.5 60
13 55.280530923261226254 37.588423673993486442 36 60
14 59.767395102644803054 42.255369424239875108 36 45 60
15 67.424848155089284364 49.663821854532241004 22.5 30 45
16 75.565544704433850714 59.876414880097563514 30 36
17 115.56968556618976742 111.14946533380144110 18 60
18 183.19554518150396045 228.17899489089532558 18 30 45
2012年8月19日
04[3,3,3,3,3] 09[5,5,5] Compounds 多面体 組物 製作道具
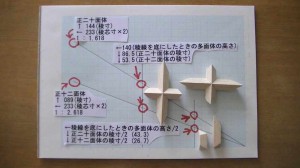
正十二面体と正二十面体との複合多面体 compounds 製作の
基本図面と その部品です。
二つの多面体を複合するには
稜から中芯点までの寸法が同じであることが必要です。
今回寸法を統一して 高さを 140mm とします。

部品の結合作業中です。

完成です この複合多面体は私にとって プロトタイプです。
すす竹では 作ろうという元気が起こりませんでした。

次回は 四つの三角リングでつくる シィメトリーな組み物を お伝えします。
準正多面体 の立法八面体とは兄弟関係にあります。
この組み物はよく目にするのですが どう呼ばれているのか知りません。
2012年6月25日
02[3,3,3,3] 03[4,4,4] Compounds 多面体 製作道具

今日は正八面体( Octahedron ) についてお伝えします
左にあるのがその完成品です。
二つの治具で加工ができます。
今回も 10×10のバルサ材を使用しています ( 寸法は 85mm)。
右端の治具で ( 角棒の直角の面をそれぞれ45度傾ける溝があり 傾斜はなし)
角棒を両端とも45度斜めにカットします。
カットされた面を見ると菱形になっています (両端のカット面は 面対象)。
そして 真ん中のクレィドル cradle で
45度斜めにカットした部品の面を垂直にし(角棒の傾斜は45度)
左右45度ずつ 90度の接合面をつくります。
下の部品のように 右の状態から 左の状態に加工し 12個つくります。
それを接着すれば あっけなく完成です。
部品数も少なく 作業も容易に見えますが 加工角度が鋭角なため
作業性を高めるために ドレサー dresser だけでなく
カッターやのこぎりで ラフ整形をします。
dresser だけの加工では
かなりの 細かい木屑が発生し まめなクリーニングが必要です。
これは レオナルドスタイルの製作のことや この用具だけのことではなく
木材加工全般にもいえることで いつも考慮すべきことです。

正八面体と正六面体の複合多面体 compounds について説明します。
下の図右がその完成品です。
以前 星型八面体の製作をお伝えしたのと同じ方法で 二つの多面体を複合します。
正八面体に対応する部分は 正八面体と同じ寸法の稜寸にしています。
しかし 正六面体は正八面体と形状が異なり
正六面体部分の稜寸を 正八面体と同寸にすると うまく稜が交差しません。
そこで 稜から中芯までの距離をそれぞれ 同じくして複合します。
正八面体の稜寸を 1としたとき 稜芯寸は 0.5 。
正六面体の稜寸を 1としたとき 稜芯寸は 0.707 。
つまり 今回正八面体の稜寸を 85としましたから 高さ85mm で
正六面体の稜寸は 60.1 になります ( 1対 0.707 )。
この比例関係を グラフ用紙に表示すると
底辺 239 (正八面体の稜寸)で 対辺 169 (正六面体の稜寸) の斜線関係となります。

次回は 正十二面体や正二十面体 そしてそれらの複合多面体について
お伝えしようかと 思っています。
2012年6月18日
01[3,3,3] Compounds 多面体 製作道具

星型八面体について説明します。
稜の寸法が同じ二つの正四面体を
稜の中心を通って稜が直角に交差するように
合体させるとできる複合多面体 compounds です。
ヨハネス ケプラー(Johannes Kepler) が発見した(?)立体で
ステラ オクタンギュラ(Stella octangula)とよばれています。
部品の説明にはいります。
青く色のついた部品は 正四面体製作部品のマザー(mother) です。
その下の二つの 対になった部品が今回必要な部品で
ひとつの端を 35.3度 の面にカットし他端は直角になっています。
斜めになった面は正四面体と同じ作業ですが 直角になったところを
左右45度ずつ 90度に先端を切削する クレィドルで加工します。
赤く汚した部品のようにして 24個作ります。

部品の材料についてお話しします。
私の過去に製作した多面体の見本として 画面に載せているのは
ほとんど 5×5 のすす竹の “さい箸” で作っています。
寸法の 2/3 ほどは 5×5 の四角柱で 1/3 ほどが円錐状に削られています。
日曜大工の 材木売り場には売っていません。
初めは近くの観光地の土産売り場で買っていました。
20本入った袋が 500円から 1000円ほどしていました。
今は 一部の百円ショップで買えるようになりました。
レオナルドスタイル(Leonardo-style) に必要な材質のお勧めは
第一はなんと言ってもバルサ材です。
ただ 5×5 で作った作品で 鑑賞に値するものはなかなかできません。
材質がやわらかくて 直線の維持がむつかしく シィメトリーにするのに 技術力がいります。
腕をみがけば 5×5 のバルサ材でも すばらしい作品ができるはずです (私はまだですが)。
その次は プラ棒です 模型や フィギュアーの加工部品として売っています。
ドレサーでの加工で
速く切削操作をすると摩擦熱で切削面がやわらかくなり 加工が楽です。
ただ接着剤には 合成ゴム系のような性質がある透明タイプのものが必要です。
それと 断面が直角三角形の プラ棒もお勧めです。
クレィドルに使う溝の作成に重宝しています。
その次は ヒノキ材でしょう そして洋材が色々あり 最後がすす竹です。
そのせいもあり 私の作品はほとんど プロトタイプで 1点ものです。

今 手元にあるバルサ材のレオナルドスタイルは これらが全てです。
製作説明の作品として これから増えてゆくでしょう。
2012年6月8日
<
1
2

















