多面体

sashimono[ 3,4,5,4 ]の双対Trapezoidal Hexecontahedron 6

14[3,4,5,4] 多面体

[ 3,4,5,4 ]の双対多面体Trapezoidal Hexecontahedron 凧形60面体の
二種類の結合部品の組合せが 完成しました。



あと一つの星型結合部品をはめれば 接合作業は完成です。
この状態で それぞれの合わさり具合を調整したりします。



少し不満は残りますが 作品完成とします。
左にある [3,4,5,4]Rhombicosidodecahedron 斜方20･12面体 は
十年以上前 すす竹を材料にして多面体製作 を始めた頃の作品です。



次回は [3,4,4,4] Rhombicuboctahedron 斜方立方8面体 (写真左)と
その双対多面体 ( Trapezoidal Icositetrahedron 凧形24面体 )とで出来る
複合多面体 compounds についてお伝えしようかと思っています。

双対多面体の Trapezoidal Icositetrahedron 凧形24面体 はすでにお伝えしています。

2013年1月10日

sashimono[ 3,4,5,4 ]の双対Trapezoidal Hexecontahedron 5

14[3,4,5,4] 多面体

準正多面体[ 3,4,5,4 ]の双対多面体 Trapezoidal Hexecontahedron の
二種類ある稜部品( 4,3形と5,4形 )つくりが完了し 接合作業にはいりました。

今回は 二種類の結合部品の組合せで　立体をつくってゆきます。
4,3形の部品を 三つ合わせた結合部品 20個 と
5,4形の部品を 五つ合わせた結合部品 12個 です。
4,3形の結合部品の接合部分は 3形で 接合角 120度 ( 360度/3 ) 仰角 07.62度です。
5,4形の結合部品の接合部分は 5形で 接合角 072度 ( 360度/5 ) 仰角 18.43度です。
この二種類の部品を作れば 接合作業は 方法を説明するまでもなく進みます。

私は 同じ作業を長く続けるのが苦手なので 完成までに 少し時間がかかります。

2013年1月9日

sashimono[ 3,4,5,4 ]の双対Trapezoidal Hexecontahedron 4

14[3,4,5,4] 多面体 製作道具

前回お伝えした 二種類ある稜部品の拡大写真です。
どちらも mother として決定したものですが 加工品質や精度は この程度です。

両面テープの破片で支え 罫線に合わせようとして 撮っています。
二本の斜線と 横線との交差部分は カッターナイフでの罫書きです。
計算では 大きいほうの寸法が 20.45mm 小さいのが 13.28mm です。

1mm という巾が かなり大きなものだと実感させられます。

2012年12月27日

sashimono[ 3,4,5,4 ]の双対Trapezoidal Hexecontahedron 3

14[3,4,5,4] 多面体 製作道具

[ 3,4,5,4 ]の双対多面体を作るのに必要な 稜部品製作の治具について今回もお伝えします。

三つある cradle は 左から 元の多面体の面 (三角形、四角形、五角形)に対応して
3形、4形、5形 の三種類です。
3形は 仰角 07.62度 接合角は 左右 60度で 120度。
4形は 仰角 13.28度 接合角は 左右 45度で 090度。
5形は 仰角 18.43度 接合角は 左右 36度で 072度 となります。

それらの下にある長方形の治具で 稜部品の寸法と切断角を決定し 切りそろえます。
今までお伝えしていた この作業の治具は 個別に作り消耗品としていましたが
これは 再利用することにより その作業を簡略にしています。

厚さ 5mm 巾 10mm の細板を 5mmずつずらせて 4枚張り合わせた受け台です。
使うごとに スリットを増やしてゆきます。
この画面では仰角 13.28度の傾斜に治具をあわせ
垂直の罫線方向に ノコギリでスリットをいれています。
これが仰角 13.28度の余角 (76.72度) になり 4形の 稜の部分をつくります。
寸法決定は 右の図から作った 基準部品の mother をもとにして治具にしるしをいれます。
これで 5,4形の稜部品の片端と 4,3形の稜部品の片端を作り、二種類のしるしが必要です。
あと 5形と3形の スリットをいれて しるしをつけています。
切断面の整形は cradle での作業で行います。

右にある小さい二つの部品は 二種類ある稜部品( 4,3形と5,4形 )の mothers です。
小さい方が 四角形と三角形をまたぐ稜の部品 ( 4,3形 ) です。
稜寸に対する 面芯寸は 0.380 対 1 ( 063 対 166 ) で罫線紙に表示。
そして大きい方が ( 5,4形 )で、
稜寸に対する 面芯寸は 0.584 対 1 ( 111 対 190 )で罫線紙に表示しています。

今回も 5×5 のすす竹で 大きさを 70mm にしようとしています。
二本の斜線と 数値 35の 位置の横線との 交点がそれぞれの実寸です。
小さい方は 15mm 以下の寸法部品をつくることになります。
作業性を高め 正確さを維持できるよう試行錯誤しながら進めてゆきます。

(カーソルを画像に置き 左クリックすれば 大きな画像が得られます。)

2012年12月26日

sashimono[ 3,4,5,4 ]の双対Trapezoidal Hexecontahedron 2

14[3,4,5,4] 多面体 製作道具

[ 3,4,5,4 ]の双対多面体 Trapezoidal Hexecontahedron 凧形60面体を作るのに必要な稜部品製作の治具についてお伝えします。

私は クレィドル cradle という用語をよく用います。小児用ベッドから由来した言葉で台座とか受け台などの治具の用語として 工業的な分野で用いられています。
そして 多面体製作の場合 稜部品の接合形状を完成させるための治具にのみcradle という用語を用いています。
また dresser を “仕上げ切削用具” の意味として用い mother という用語は “基準となる参照部品” という意味で使っています。



cradle の傾斜部品を作ろうとしています。
Trapezoidal Hexecontahedron 凧形60面体は 双対多面体ですので 仰角は 複数存在します。
今回は三種類必要です。
元の多面体の 五角形の中心の上にくる部品を作る仰角は 18.43度
元の多面体の 四角形の中心の上にくる部品を作る仰角は 13.28度
元の多面体の 三角形の中心の上にくる部品を作る仰角は 7.62度です。

罫線上での角度表示は
18.43度が 座標0,0 の位置から 縦 83 横 249 の位置に線を描きます。
画面では三本ある斜線の一番角度のきつい斜線です。
その線に沿って傾斜部品を整形する治具を作っています。

その下の斜線が 13.28度で
座標0,0 の位置から 縦 55 横 233 の位置に線を描いています。

一番下の斜線で 厚み15mm のバルサ材の切り出し角度を確認しています。
7.62度で 座標0,0 の位置から 縦 19 横 142 の位置に線を描いています。

私は 数値計算をする場合
表計算ソフトなど パソコンのソフトを用いて行っていますが
タンジェントの確認や 手軽な計算用具としては関数電卓を用いています。
私が 多面体を作り始めた頃は 関数電卓は \10,000 では到底買えませんでした。
指数表示や 三角関数の演算ができれば いいのです。
今では \1,000 でお釣がきます。関数電卓は 多面体製作には お勧めです。

2012年12月23日

sashimono[ 3,4,5,4 ]の双対Trapezoidal Hexecontahedron 1

14[3,4,5,4] 多面体 諸量

[ 3,4,5,4 ] Rhombicosidodecahedron 斜方20･12面体 と
Trapezoidal Hexecontahedron 凧形60面体の諸量を表記しておきます。

14　[3,4,5,4]Rhombicosidodecahedron 斜方20･12面体
14　.97460776237817045237　[3,4,5,4]基本数
14　12.939318437111839760　[3,4,5,4]仰角( 051/222 )
14　2.2329505094156900495　[3,4,5,4]頂芯寸( 230/103 )
14　2.1762508994828215111　[3,4,5,4]稜芯寸( 222/102 )
14　56.108494226282325602　[3,4,5,4]5 接合角( 131/088 )
14　46.512922254478226490　[3,4,5,4]4 接合角( 136/129 )
14　30.865661264761221417　[3,4,5,4]3 接合角( 104/174 )
14　2.0645728807067603073　[3,4,5,4]5 面芯寸( 192/093 )
14　2.1180339887498948482　[3,4,5,4]4 面芯寸( 233/110 )
14　2.1570198525202442752　[3,4,5,4]3 面芯寸( 151/070 )
14　59.305982844911989541　[3,4,5,4]面積
14　41.615323782497967065　[3,4,5,4]体積
14　71.565051177077989352　[3,4,5,4]5 面角
14　76.717474411461005324　[3,4,5,4]4 面角
14　82.377368140649695643　[3,4,5,4]3 面角
14　148.28252558853899468　[3,4,5,4]5 4 面角
14　159.09484255211070097　[3,4,5,4]4 3 面角
14　[3,4,5,4] 5 4 個数 60
14　[3,4,5,4] 4 3 個数 60

14　双対[3,4,5,4]Trapezoidal Hexecontahedron 凧形60面体
14　154.12136312577632048　双[3,4,5,4]二面角
14　2.1209910195184334175　双[3,4,5,4]面芯寸( 193/091 )
14　18.434948822922010648　双[3,4,5,4]5 仰角( 083/249 )
14　13.282525588538994676　双[3,4,5,4]4 仰角( 055/233 )
14　7.6226318593503043571　双[3,4,5,4]3 仰角( 019/142 )
14　.72541696649427383703　双[3,4,5,4]5 稜寸( 177/244 )
14　.51374314837300779674　双[3,4,5,4]4 稜寸( 112/218 )
14　.29124883602080337314　双[3,4,5,4]3 稜寸( 060/206 )
14　67.783011547435348796　双[3,4,5,4]5 かど角
14　86.974155491043547019　双[3,4,5,4]4 かど角
14　118.26867747047755717　双[3,4,5,4]3 かど角
14　2.2939698674519558970　双[3,4,5,4]5 頂芯寸( 234/102 )
14　2.2360679774997896964　双[3,4,5,4]4 頂芯寸( 161/072 )
14　2.1956534020612776371　双[3,4,5,4]3 頂芯寸( 202/092 )
14　59.767395102644803054　双[3,4,5,4]面積
14　42.255369424239875108　双[3,4,5,4]体積
14　36.000000000000000000　双[3,4,5,4]5 接合角/2( 178/245 )
14　45.000000000000000000　双[3,4,5,4]4 接合角/2( 180/180 )
14　60.000000000000000000　双[3,4,5,4]3 接合角/2( 194/112 )
14　1.2391601148672816338　双[3,4,5,4]5 4 稜寸( 171/138 )
14　.80499198439381116988　双[3,4,5,4]4 3 稜寸( 161/200 )
14　.58423637981674733850　双[3,4,5,4]5 4 稜寸/面芯寸( 111/190 )
14　.37953578161617248109　双[3,4,5,4]4 3 稜寸/面芯寸( 063/166 )
14　双[3,4,5,4] 5 4 個数 60
14　双[3,4,5,4] 4 3 個数 60

2012年12月19日

sashimono[3,3,3,3,4] の双対多面体Pentagonal Icositetrahedron 4

07[3,3,3,3,4] 多面体

[3,3,3,3,4] の双対多面体の Pentagonal Icositetrahedron 五角24面体を作っています。

5×5 のすす竹で 完成品の大きさは 70mm の予定です。
二つの cradleで 二種類 ( 3,3形 3,4形) の部品を作っています。
3,3形は 寸法の小さい方で 右下の cradleで 36個作ります。
接合面が 60度＋60度 仰角は 13.38度( 059/248 )で両端を加工します。

3,4形は 寸法の大きい方で 右の二つの cradleで 24個作ります。
片端の接合面や仰角は 3,3形と同じに加工し、
もう片端は 45度＋45度 仰角 23.63度( 105/240 )で加工します。

この多面体も 鏡像体があり 部品の接合方法は
[3,3,3,3,5] の双対多面体 Pentagonal Hexecontahedron 五角60面体と同じです。
結合部品 (Ｎ形 Ｓ形) があり どちらか一方の部品の集合12セットで多面体が完成します。
小さい部品 (3,3形) 三つでＮのような形に接合しそれに長い部品 (3,4形) を二つ結合させたＮ形を作るタイプと。
小さい部品 (3,3形) 三つでＳのような形に接合しそれに長い部品 (3,4形) を二つ結合させたＳ形 があります。
今回は Ｓ形の結合部品の組合せで作業を進めています。



[3,3,3,3,4]の 準正多面体と 双対多面体の製作が完成しました。
右の図は 以下の数値をもとに底辺の数値 35で 対辺から 稜の部品の実寸を決定しています。

07　.72776796213464204867　双[3,3,3,3,4]4 3 稜寸/面芯寸( 131/180 )
07　.51264139544774378927　双[3,3,3,3,4]3 3 稜寸/面芯寸( 081/158 )

次回は [ 3,4,5,4 ] Rhombicosidodecahedron 斜方20･12面体の双対多面体
Trapezoidal Hexecontahedron 凧形60面体についてお伝えします。

2012年12月19日

sashimono[3,3,3,3,4] Snub Cube 変形立方体 とその双対 3

07[3,3,3,3,4] 多面体

[3,3,3,3,4] Snub Cubeの 部品製作が完了し 組み立て作業をしています。

5×5 のすす竹で 完成品の大きさは 四角形を底にして 70mm の予定です。
部品寸法は　約30.6mmです。( 35 ÷ 1.143 = 30.621 )

二つの cradleで 二種類(3,3形 3,4形) の部品を作っています。
どちらも 仰角は 21.85度です。
部品を縦方向に置いた場合
三角形をつくる接合面が左右 上下ともにあるもの (3,3形) が 36個と
片側 上下が 三角形を そして他の側の上下が四角形をつくるもの (3,4形) が 24個です。

この多面体には [3,3,3,3,5]と同じく 鏡像体が存在します。
そのため 接合作業で 同じような混乱が生じる場合があります。
これを避けるために
三つの部品 (3,3形) を S状につなげて 二つの部品 (3,4形) を添える方法と
三つの部品 (3,3形) を N状につなげて 二つの部品 (3,4形) を添える方法があります。
S形に 3,4形二つを結合して 三角形二個つなげた基本結合部品と
N形に 3,4形二つを結合して 三角形二個つなげた基本結合部品との
どちらか一方の基本結合部品12個 の組合せで 多面体 [3,3,3,3,4] が完成します。

今回も N形のほうで結合を進めています。



完成しました。　手前は 以前作った [3,3,3,3,5]です。

2012年12月16日

sashimono[3,3,3,3,4] Snub Cube 変形立方体 とその双対 2

07[3,3,3,3,4] 多面体 製作道具

[3,3,3,3,4] Snub Cube の製作道具を作っているところです。

図右の 二つの傾斜部品は 対辺 91 底辺 227 で表わされる 21.85度の仰角固定部品。
その横が 対辺 147 底辺 125 で表わされる 49.62度×2で左右対称な 接合角固定部品。
図左が 対辺 156 底辺 244 で表わされる 32.59度×2で左右対称な 接合角固定部品です。



双対多面体 [3,3,3,3,4] Pentagonal Icositetrahedron の製作道具を作っているところです。

図右の 傾斜部品は 対辺 59 底辺 248 で表わされる 13.38度の仰角固定部品。
その横が 対辺 194 底辺 112 で表わされる 60.00度×2で左右対称な 接合角固定部品。
図左の 傾斜部品は 対辺 105 底辺 240 で表わされる 23.63度の仰角固定部品。
その横が 対辺 180 底辺 180 で表わされる 45.00度×2で左右対称な 接合角固定部品です。



写真左 上と下 は [3,3,3,3,4] 準正多面体 Snub Cube 製作のcradle です。
上は 四角形に接する稜を作り 21.85度の仰角 49.62度×2で左右対称な 接合角。
下は 三角形に接する稜を作り 21.85度の仰角 32.59度×2で左右対称な 接合角です。

写真右 上と下 は [3,3,3,3,4] 双対多面体 Pentagonal Icositetrahedron 製作のcradle です。
まだ稜部品先端の加工部分の整形が済んでいません。
上は 四角形の上にくる稜を作り 23.63度の仰角 45.00度×2で左右対称な 接合角。
下は 三角形の上にくる稜を作り 13.38度の仰角 60.00度×2で左右対称な 接合角です。

2012年12月10日

sashimono[3,3,3,3,4] Snub Cube 変形立方体 1

07[3,3,3,3,4] 多面体 諸量

[3,3,3,3,4] Snub Cube 変形立方体 と
その双対多面体の　Pentagonal Icositetrahedron 五角24面体 の諸量を表示します。

07　[3,3,3,3,4] Snub Cube 変形立方体
07　.92819137798557160941　07[3,3,3,3,4]基本数
07　21.845383553837898091　07[3,3,3,3,4]仰角( 091/227 )
07　1.3437133737446017013　07[3,3,3,3,4]頂芯寸( 215/160 )
07　1.2472231679936432518　07[3,3,3,3,4]稜芯寸( 222/178 )
07　49.624148955803785616　07[3,3,3,3,4]4 接合角( 147/125 )
07　32.593962761049053596　07[3,3,3,3,4]3 接合角( 156/244 )
07　1.1426135089259620935　07[3,3,3,3,4]4 面芯寸( 200/175 )
07　1.2133558000218923103　07[3,3,3,3,4]3 面芯寸( 182/150 )
07　19.856406460551018348　07[3,3,3,3,4]面積
07　7.8894773999753902065　07[3,3,3,3,4]体積
07　66.366136216794602533　07[3,3,3,3,4]4 面角
07　76.617293856710015509　07[3,3,3,3,4]3 面角
07　142.98343007350461804　07[3,3,3,3,4]4 3 面角
07　153.23458771342003102　07[3,3,3,3,4]3 3 面角
07　[3,3,3,3,4] 4 3 個数 24
07　[3,3,3,3,4] 3 3 個数 36

07　双対[3,3,3,3,4] Pentagonal Icositetrahedron 五角24面体
07　136.30923289232420382　双[3,3,3,3,4]二面角
07　1.1576617909555498021　双[3,3,3,3,4]面芯寸( 191/165 )
07　23.633863783205397467　双[3,3,3,3,4]4 仰角( 105/240 )
07　13.382706143289984491　双[3,3,3,3,4]3 仰角( 059/248 )
07　.54577648445886681200　双[3,3,3,3,4]4 稜寸( 131/240 )
07　.29673267798599365525　双[3,3,3,3,4]3 稜寸( 073/246 )
07　80.751702088392428768　双[3,3,3,3,4]4 かど角
07　114.81207447790189281　双[3,3,3,3,4]3 かど角
07　1.3614101519264425345　双[3,3,3,3,4]4 頂芯寸( 226/166 )
07　1.2820358469890142117　双[3,3,3,3,4]3 頂芯寸( 200/156 )
07　19.299406563296038279　双[3,3,3,3,4]面積
07　7.4473951888148613654　双[3,3,3,3,4]体積
07　45.000000000000000000　双[3,3,3,3,4]4 接合角/2( 180/180 )
07　60.000000000000000000　双[3,3,3,3,4]3 接合角/2( 194/112 )
07　.84250916244486046725　双[3,3,3,3,4]4 3 稜寸( 107/127 )
07　.59346535597198731050　双[3,3,3,3,4]3 3 稜寸( 127/214 )
07　.72776796213464204867　双[3,3,3,3,4]4 3 稜寸/面芯寸( 131/180 )
07　.51264139544774378927　双[3,3,3,3,4]3 3 稜寸/面芯寸( 081/158 )
07　双対[3,3,3,3,4] 4 3 個数 24
07　双対[3,3,3,3,4] 3 3 個数 36

2012年12月5日

sashimono[5,6,6]の双対多面体 Pentakis Dodecahedron 3

16[5,6,6] 多面体

Pentakis Dodecahedron 五方12面体 がもう少しでできます。
組み立ての 秘訣は 六角形と五角形をまたぐ稜の部品を星型にして 12個作ります。
そして星型と星型とを 六角形と六角形をまたぐ稜部品を間にして 組み合わせて行きます。



接着作業は終わりました。接合面の微調整をし 接着剤のはみ出しを取ります。

右側の Truncated Icosahedron は この Pentakis Dodecahedron と一緒に作っていました。
5×5 のすす竹で 約 70mm の大きさです。

次回は [3,3,3,3,4] Snub Cube 変形立方体 と
その双対多面体の　Pentagonal Icositetrahedron 五角24面体 について お伝えします。

2012年12月4日

sashimono[5,6,6]の双対多面体 Pentakis Dodecahedron 2

16[5,6,6] 多面体 製作道具

[5,6,6]の双対多面体の製作準備をしているところです。
部品製作の方法を伝える場合 双対多面体は 元の多面体の構造を基準として説明します。

この多面体に必要な部品は
六角形と六角形をまたぐ部品と 六角形と五角形をまたぐ部品の二種類です。

六角形と六角形をまたぐ部品は 元の多面体の稜寸を 1とした場合 1.854 の稜寸。
部品の両端は六角形の中心の上に来て 左右それぞれ 30度 の接合角で仰角は 20.91度。
30個必要です。

六角形と五角形をまたぐ部品は 元の多面体の稜寸を 1とした場合 1.645 の稜寸。
片端が 六角形の中心の上に来て 左右それぞれ 30.00度 の接合角で仰角は 20.91度。
もう一つの端は 五角形の中心の上に来て
左右それぞれ 36.00度 の接合角で仰角は 16.47度。60個必要です。

次に稜の寸法の決定についてお伝えします。
完成の多面対の面芯寸を 1 とすると
六角形と六角形をまたぐ部品の稜寸は 0.7800。0.7800 対 1 は 156 対 200です。
六角形と五角形をまたぐ部品の稜寸は 0.6919。0.6919 対 1 は 128 対 185です。
二つの部品の寸法の比例関係を正確にするために 罫線紙から求めます。
六角形と六角形をまたぐ部品の場合は
縦方向に 200 横方向に 156 の点に 座標 0,0 から斜線をプロットします。
六角形と五角形をまたぐ部品の場合は
縦方向に 185 横方向に 128 の点に 座標 0,0 から斜線をプロットします。
完成の多面体の高さを 70mm としていますので 面芯寸を 35mm とします。
縦方向に 35の位置から横方向に向けた直線と斜線の交点から
それぞれの稜寸が 実寸として得られます。
六角形と六角形をまたぐ部品の稜寸は 0.7800×35 で 27.30mm。
六角形と五角形をまたぐ部品の稜寸は 0.6919×35 で 24.22mm のはずです。
この操作を 写真右の用紙で行っています。

写真左の用紙で 六角形の上に来る部品の cradle を作ろうとしています。
左右それぞれ 30度 の接合角で仰角は 20.91度。
30.00度のタンジェントは 112/194。20.91度のタンジェントは 089/233 です。

写真中の用紙で 五角形の上に来る部品の cradle を作ろうとしています。
左右それぞれ 36.00度 の接合角で仰角は 16.47度。
36.00度のタンジェントは 178/245。16.47度のタンジェントは 055/186 です。

2012年11月30日

sashimono[5,6,6]の双対多面体 Pentakis Dodecahedron 1

16[5,6,6] 多面体

[5,6,6] Truncated Icosahedron 切頂20面体 (サッカーボール)の
双対多面体 Pentakis Dodecahedron 五方12面体 についてお伝えします。
すす竹 5×5 で 高さ約70mm の立体模型をつくる予定です。
すでにお伝えしている Truncated Icosahedron 切頂20面体も含めて
諸量を表示します。

16　[5,6,6] Truncated Icosahedron 切頂20面体
16　.97943208548641418658　16[5,6,6]基本数
16　11.640723136770606678　16[5,6,6]仰角( 048/233 )
16　2.4780186590676155376　16[5,6,6]頂芯寸( 223/090 )
16　2.4270509831248422723　16[5,6,6]稜芯寸( 233/096 )
16　62.154680232796997218　16[5,6,6]6 接合角( 248/131 )
16　55.690639534406005565　16[5,6,6]5 接合角( 233/159 )
16　2.2672839422285121914　16[5,6,6]6 面芯寸( 229/101 )
16　2.3274384367663271103　16[5,6,6]5 面芯寸( 135/058 )
16　72.607253034133921879　16[5,6,6]面積
16　55.287730758122739236　16[5,6,6]体積
16　69.094842552110700967　16[5,6,6]6 面角
16　73.527789307239603390　16[5,6,6]5 面角
16　138.18968510422140193　16[5,6,6]6 6 面角
16　142.62263185935030436　16[5,6,6]6 5 面角
16　[5,6,6] 6 6 個数 30, 6 5 個数 60

16　双[5,6,6] Pentakis Dodecahedron 五方12面体
16　156.71855372645878664　双[5,6,6]二面角
16　2.3771316059838161118　双[5,6,6]面芯寸( 145/061 )
16　20.905157447889299033　双[5,6,6]6 仰角( 089/233 )
16　16.472210692760396610　双[5,6,6]5 仰角( 055/186 )
16　.92705098312484227231　双[5,6,6]6 稜寸( 178/192 )
16　.71764499555916901903　双[5,6,6]5 稜寸( 122/170 )
16　55.690639534406005565　双[5,6,6]6 かど角
16　68.618720931187988871　双[5,6,6]5 かど角
16　2.5980762113533159403　双[5,6,6]6 頂芯寸( 239/092 )
16　2.5309268686270615215　双[5,6,6]5 頂芯寸( 205/081 )
16　75.565544704433850714　双[5,6,6]面積
16　59.876414880097563514　双[5,6,6]体積
16　30.000000000000000000　双[5,6,6]6 接合角/2( 112/194 )
16　36.000000000000000000　双[5,6,6]5 接合角/2( 178/245 )
16　1.8541019662496845446　双[5,6,6]6 6 稜寸( 178/096 )
16　1.6446959786840112913　双[5,6,6]6 5 稜寸( 250/152 )
16　.77997447073711053264　双[5,6,6]6 6 稜寸/面芯寸( 156/200 )
16　.69188259267762587725　双[5,6,6]6 5 稜寸/面芯寸( 128/185 )
16　双[5,6,6] 6 6 個数 30, 6 5 個数 60

2012年11月30日

sashimono[3,5,3,5]の複合多面体 4

11[3,5,3,5] Compounds 多面体

Icosidodecahedron 20･12面体 と Rhombic Triacontahedron 菱形30面体 との
複合多面体 compounds の製作途中です。



組み立て作業は終わりました。これから微調整をします。
高さは約 160mm 5×5 のすす竹です。
準正多面体 の複合多面体の製作は 今回が初めてでした。
しかし組み立て方法は簡単です。
Icosidodecahedron や Rhombic Triacontahedron を
作った経験があれば 説明するまでもないと思います。
始めにお伝えしました 十字架状の結合部品の組合せで完成します。

次回は [5,6,6] Truncated Icosahedron 切頂20面体 (サッカーボール)の
双対多面体 Pentakis Dodecahedron 五方12面体 についてお伝えしようと思っています。

2012年11月20日

sashimono[3,5,3,5]の複合多面体 3

11[3,5,3,5] Compounds 多面体 製作道具

[3,5,3,5]複合多面体 compounds の寸法の決定についてお伝えします。

[3,5,3,5]多面体と [3,5,3,5]双対多面体の稜芯寸を
同じ値にしなければなりません。

高さを約 160mm に予定をしていましたので、稜芯寸を 80mmとします。

それそれれの稜の寸法を得るために
稜寸と 稜芯寸の比を表わす直線を方眼紙に描きます。

[3,5,3,5]多面体の稜寸と稜芯寸の比は 1 対 1.5388 ( 154/237 ) ですが
稜の中間点で [3,5,3,5]双対多面体の稜と直角に交差するため
対辺 154 の 1/2 の 77 で 底辺 237 の斜線を引きます。
画面にある 3本の斜線の 真ん中の線がそれです。

3本の斜線の右側のが 対辺 125 底辺 250 で 5角形の中心の上にくる稜の比です。
3本の斜線の左側のが 対辺 034 底辺 178 で 3角形の中心の上にくる稜の比です。

縦方向に下から 80の座標の横線と斜線の交点からそれぞれの値が得られます。
この図では より正確な値を得るために 縦線 横線 斜線の必要部分を
カッターナイフで処理しています。実寸で 40.0mm 26.0mm 15.3mm となります。

左上の cradleで 平面に 45度+45度の角度ですべての稜部品の片側を整形します。
その下の ペアーの cradleで26.0mmの部品を 仰角 18度の傾斜で加工します。

左に接合角 58.28度 右に接合角 31.72度で 60個と、
右に接合角 58.28度 左に接合角 31.72度で 60個必要です。

右上の cradleで 40.0mmの部品を 26.57度の仰角で 60個加工します。
その下の cradleで 15.3mmの部品を 10.81度の仰角で 60個加工します。

これらの 4種類の形状部品で 画面にある十字架状の 結合部品を 60個つくります。
これを接着してゆけば 複合多面体が完成します。そのはずです。

この [3,5,3,5]複合多面体は 私にとって初めての製作です。
急いだり、作業に飽きたりして 品質の良くない部品を作らないよう、
ゆっくりと作ってゆこうと思っています。

11 1.5388     [3,5,3,5] 稜寸を 1としたときの稜芯寸           ( 237/154 )
11 .50000 双対[3,5,3,5] 5角形の中心の上にくる稜の寸法/稜芯寸 ( 125/250 )
11 .19098 双対[3,5,3,5] 3角形の中心の上にくる稜の寸法/稜芯寸 ( 034/178 )

2012年11月11日

sashimono[3,5,3,5]の複合多面体 2

11[3,5,3,5] Compounds 多面体 製作道具

[3,5,3,5]の複合多面体 compounds の製作に必要な治具です。

高さを約 160mm にして 5×5 のすす竹でつくる予定をしています。

今回は [3,5,3,5]多面体と[3,5,3,5]双対多面体の
稜の部材の形状加工についてです。
再びの説明となります。寸法の決定については 次回にお伝えします。

三枚あるA4の方眼紙の内の左の方眼紙の中に [3,5,3,5]多面体の治具があります。

方眼紙の左下かどから上方向 233 右方向 144の座標に線をひき、
そして 左上かどから下方向 233 右方向 144の座標に線をひき
58.28度を上下対称にプロットしています。
これが 5角形の接合角です。

この角度と90度との差(余角) が3角形の接合角(31.72度) になります。
つまり 5角形の接合角と 3角形の接合角を合計すると 丁度 90度です。

この方眼紙の右にある三角形ふたつの部材は15mmの厚みのバルサ材で、
対辺 077 底辺 237 でできる 仰角 18度の傾斜です。

これらの上にある 四角形の部材が
仰角18度の余角(72度)で切断面をつくり 寸法や形状を整える治具です。
そして cradleの傾斜の溝にする部材が 2セット写っています。

この多面体には 二種類のcradleが必要です。
左に接合角 58.28度 右に接合角 31.72度のcradleと、
右に接合角 58.28度 左に接合角 31.72度のcradleとです。

つづいて この方眼紙の右の二枚の方眼紙の説明をします。
この二つで [3,5,3,5]双対多面体のcradleを作ります。

二つの内の左側の図で
5角形の中心の上にくる稜を製作するためのcradleを作ります。
方眼紙の左下かどから 右方向 178 上方向 245の座標に線をひき、
そして左右対称に 右下かどから 左方向 178 上方向 245の座標に線をひき、
5角形の上の接合角 36.00度×2 をプロットしています。

傾斜の部材は 対辺 125 底辺 250 でできる 26.57度の仰角です。

二つの内の右側の図で
3角形の中心の上にくる稜を製作するためのcradleを作ります。
方眼紙の左下かどから上方向 194 右方向 112の座標に線をひき、
そして上下対称に 左上かどから下方向 194 右方向 112の座標に線をひき、
3角形の上の接合角 60.00度×2 をにプロットしています。

傾斜の部材は 対辺 034 底辺 178 でできる 10.81度の仰角です。

11 58.283 [3,5,3,5] 5角形の接合角 ( 233/144 )
11 31.717 [3,5,3,5] 3角形の接合角 ( 144/233 )
11 18.000 [3,5,3,5] 稜の仰角 ( 077/237 )
11 36.000 双対[3,5,3,5] 5角形の中心の上にくる稜の接合角/2 ( 360/5度/2　178/245 )
11 26.565 双対[3,5,3,5] 5角形の中心の上にくる稜の仰角 ( 125/250 )
11 60.000 双対[3,5,3,5] 3角形の中心の上にくる稜の接合角/2 ( 360/3度/2　194/112 )
11 10.812 双対[3,5,3,5] 3角形の中心の上にくる稜の仰角 ( 034/178 )

2012年11月9日

sashimono[3,5,3,5]の複合多面体 1

11[3,5,3,5] Compounds 多面体

[3,5,3,5]多面体と[3,5,3,5]双対多面体との諸量をもとに
複合多面体 compounds を作ってゆきます。

すでに諸量は お伝えしているのですが表示や説明が 稚拙だったと反省しています。
改めてお伝えします。

[3,5,3,5]の諸量です。

11        Icosidodecahedron 20･12面体
11 .95106 [3,5,3,5] 基本数
11 18.000 [3,5,3,5] 稜の仰角 ( 077/237 )
11 58.283 [3,5,3,5] 5角形の接合角 ( 233/144 )
11 31.717 [3,5,3,5] 3角形の接合角 ( 144/233 )
11 1.6180 [3,5,3,5] 稜寸を 1としたときの頂芯寸 ( 233/144 )
11 1.5388 [3,5,3,5] 稜寸を 1としたときの稜芯寸 ( 237/154 )
11 1.3764 [3,5,3,5] 稜寸を 1としたときの 5角形の面芯寸 ( 245/178 )
11 1.5115 [3,5,3,5] 稜寸を 1としたときの 3角形の面芯寸 ( 198/131 )
11 60     [3,5,3,5] 5角形と 3角形の間の稜の必要個数
11 29.305982844911989541 [3,5,3,5] 稜寸を 1としたときの面積
11 13.835525936249404140 [3,5,3,5] 稜寸を 1としたときの体積

[3,5,3,5]双対多面体 Rhombic Triacontahedron の諸量です。

寸法は もとの多面体 Icosidodecahedron の稜寸が 1のとき、
複合多面体となる寸法にしています。つまり 稜芯寸が同じです。
もとの多面体の 3角形や5角形の位置をもとに計算しています。

11        Rhombic Triacontahedron 菱形30面体
11 26.565 双対[3,5,3,5] 5角形の中心の上にくる稜の仰角 ( 125/250 )
11 10.812 双対[3,5,3,5] 3角形の中心の上にくる稜の仰角 ( 034/178 )
11 36.000 双対[3,5,3,5] 5角形の中心の上にくる稜の接合角/2 ( 360/5度/2　178/245 )
11 60.000 双対[3,5,3,5] 3角形の中心の上にくる稜の接合角/2 ( 360/3度/2　194/112 )
11 1.4635 双対[3,5,3,5] 面芯寸 ( 221/151 )
11 1.5388 双対[3,5,3,5] 稜芯寸 ( 237/154 )
11 .76942 双対[3,5,3,5] 5角形の中心の上にくる稜の寸法 ( 177/230 )
11 .29389 双対[3,5,3,5] 3角形の中心の上にくる稜の寸法 ( 072/245 )
11 .50000 双対[3,5,3,5] 5角形の中心の上にくる稜の寸法/稜芯寸 ( 125/250 )
11 .19098 双対[3,5,3,5] 3角形の中心の上にくる稜の寸法/稜芯寸 ( 034/178 )
11 1.0633 双対[3,5,3,5] 5角形と3角形をまたぐ稜の寸法 ( 168/158 )
11 .72654 双対[3,5,3,5] 5角形と3角形をまたぐ稜の寸法/面芯寸 ( 178/245 )
11 60     双対[3,5,3,5] 5角形と3角形をまたぐ稜の必要個数
11 30.338137289060528404 双対[3,5,3,5] 面積
11 14.800212429686842801 双対[3,5,3,5] 体積

2012年11月3日

sashimono[3,6,6]の双対多面体 Triakis Tetrahedron 三方4面体 3

06[3,6,6] 多面体

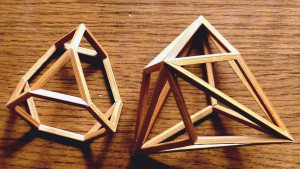
[3,6,6]の双対多面体 Triakis Tetrahedron 製作が完成です。
左の[3,6,6] Truncated Tetrahedron 切頂4面体と この大きさで複合多面体ができます。

材質は 5×5 のすす竹です。鋭い面の角度 (60度) の加工にてこずりました。
[3,6,6]の複合多面体の製作には 上の二つの多面体を作る行程数と、
それにそれぞれの稜を直角に交差させるための加工作業が加わります。
複合多面体の製作については しばらく後にお伝えしようかとおもいます。

次回は 最初のブログで お伝えした、
11 [3,5,3,5]　Icosidodecahedron 20･12面体　
11 双対[3,5,3,5]　Rhombic Triacontahedron 菱形30面体　

の 複合多面体について説明しようかと思っています。

2012年11月3日

sashimono[3,6,6]の双対多面体 Triakis Tetrahedron 三方4面体 2

06[3,6,6] 多面体 製作道具

[3,6,6]の双対多面体製作に必要な 図面と治具です。

左の図にあるのが
片方の接合角が 60度 両方を合わせて 120度の cradleと、
片方の接合角が 30度 両方を合わせて 060度の cradleです。
角度決定は 対辺 112 底辺 194 で 上下対象に角度 60＋60 をプロットしています。
その余角の 対辺 194 底辺 112 の斜線で 左右対称に角度 30＋30 が得られます。

06 60.000 双対[3,6,6] もとの多面体の3角形の上の稜の接合角 ( 180/3度 194/112 )
06 30.000 双対[3,6,6] もとの多面体の6角形の上の稜の接合角 ( 180/6度 112/194 )

06 15.793 双対[3,6,6] もとの多面体の3角形の上の稜の仰角 ( 056/198 )

06 54.736 双対[3,6,6] もとの多面体の6角形の上の稜の仰角 ( 239/169 )

06 1.1023 双対[3,6,6] もとの多面体の6角形と3角形をまたぐ稜寸 / 基準高 ( 194/176 )
06 1.8371 双対[3,6,6] もとの多面体の6角形と6角形をまたぐ稜寸 / 基準高 ( 248/135 )

2012年10月31日

sashimono[3,6,6]の双対多面体 Triakis Tetrahedron 三方4面体 1

06[3,6,6] Compounds 多面体

[3,6,6]の双対多面体 Triakis Tetrahedron 三方4面体 の製作についてお伝えします。

[3,6,6]双対多面体製作に必要な諸量です。
寸法は もとの多面体 Truncated Tetrahedron の稜寸が 1のとき、
複合多面体 compounds となる寸法にしています。つまり 稜芯寸が同じです。

06 .61237 [3,6,6]　もとの多面体の稜寸を 1としたとき その 6角形の面芯寸
06 1.0206 [3,6,6]　もとの多面体の稜寸を 1としたとき その 3角形の面芯寸
06 1.6330 [3,6,6]　もとの多面体の稜寸を 1としたとき上の二つの値の合計。

つまり多面体[3,6,6]の高さ ( 178/109 の比例関係 )であり、これを "基準高" とします。

06 54.736 双対[3,6,6]　もとの多面体の6角形の上の稜の仰角　( 239/169 )
06 15.793 双対[3,6,6]　もとの多面体の3角形の上の稜の仰角　( 056/198 )
06 30.000 双対[3,6,6]　もとの多面体の6角形の上の稜の接合角　( 180/6度 112/194 )
06 60.000 双対[3,6,6]　もとの多面体の3角形の上の稜の接合角　( 180/3度 194/112 )
06 1.5000 双対[3,6,6]　もとの多面体の6角形の上の稜寸
06 .30000 双対[3,6,6]　もとの多面体の3角形の上の稜寸
06 1.8000 双対[3,6,6]　もとの多面体の6角形と3角形をまたぐ稜寸
06 1.1023 双対[3,6,6]　もとの多面体の6角形と3角形をまたぐ稜寸 / 基準高 ( 194/176 )
06 3.0000 双対[3,6,6]　もとの多面体の6角形と6角形をまたぐ稜寸
06 1.8371 双対[3,6,6]　もとの多面体の6角形と6角形をまたぐ稜寸 / 基準高 ( 248/135 )
06 17.909773867919159185　双対[3,6,6]　面積
06 5.7275649276110349476　双対[3,6,6]　体積
06 双対[3,6,6]　もとの多面体の6角形と3角形をまたぐ稜の必要個数は 12
06 双対[3,6,6]　もとの多面体の6角形と6角形をまたぐ稜の必要個数は 06

以下の値は複合多面体製作に必要な諸量です。

06 .30619 [3,6,6]    　もとの多面体の稜寸 / 基準高 / 2 ( 064/209 )
06 .91856 双対[3,6,6]　もとの多面体の6角形の上の稜寸 / 基準高 ( 158/172 )
06 .18371 双対[3,6,6]　もとの多面体の3角形の上の稜寸 / 基準高 ( 045/245 )

2012年10月28日