sashimono[3,4,4,4] 斜方立方8面体の双対 4
組み立て作業中です。
アップにすると欠点が目立ちますが 完成しました。
2012年9月9日
RECENT POSTS
sashimono[3,4,4,4] 斜方立方8面体の双対 3
[3,4,4,4]双対多面体製作に必要な
二種類のクレィドル cradle とその加工完成部品です。
左側の cradle で [3,4,4,4]準正多面体 の四角形面の中心の上で稜が
四本集まる双対多面体部品を加工します。
接合面は 左右それぞれ 45度 仰角は 22.5度です。
右側の cradle で [3,4,4,4]準正多面体 の三角形面の中心の上で稜が
三本集まる双対多面体部品を加工します。
接合面は 左右それぞれ 60度 仰角は 12.8度です。
四角形と四角形を渡る部品を 24個作ります。
接合面はどちらの側も両面とも 45度で合わせて 90度です。
四角形と三角形を渡る部品を 24個作ります。
接合面は片側が両面とも 45度で合わせて 90度になり
もう一方の片側が両面とも 60度で合わせて 120度になります。
2012年9月8日
sashimono[3,4,4,4] 斜方立方8面体の双対 2
[3,4,4,4]の双対多面体(Trapezoidal Icositetrahedron ) の二種類の部材を
接合面の角度整形前の状態にカットしたものです (今回は すす竹風の箸を使っています)。
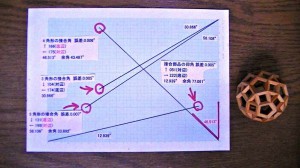
この双対多面体の面芯寸を 35mm として寸法決めをしています。
つまり 完成品の高さが 70mm になるように 部材の長さを決めています。
右上のかたまりは 双対多面体のもとの多面体の四角形ふたつをまたぐ稜で
31.05mmの寸法です。
双対多面体の面芯寸 1に対し 0.8870 の関係にあり ( 239 : 212 )
背景のグラフの右側の斜線で 表示しています。
横線の高さが 35 であり 斜線との交点が 31.05 になります。
画面下のかたまりは 双対多面体のもとの多面体の四角形と三角形をまたぐ稜で
24.01mmの寸法です。
双対多面体の面芯寸 1に対し 0.6861 の関係にあり ( 172 : 118 )
背景のグラフの左側の斜線で 表示しています。
横線の高さが 35 であり 斜線との交点が 24.01 になります。
大きい方の稜のカット面は 双対多面体のもとの多面体の四角形の面角です。
小さい方の稜のカット面は 双対多面体のもとの多面体の四角形の面角を片方にもち
三角形の面角をもう一方にもちます。
部材の必要個数は どちらも 24個です。
2012年9月2日
sashimono[3,4,4,4] 斜方立方8面体とその双対
やっと 双対多面体の説明を始めます。
写真左が 斜方立方8面体(Rhombicuboctahedron) という準正多面体 で
右がその双対多面体の凧形24面体(Trapezoidal Icositetrahedron ) です。
右と左の多面体を稜芯寸を同じくして合体させると
複合多面体 compounds になりますが
それをイメージし易いように 向きを合わせて撮っています。
左の多面体の四角形や三角形の中心の上に 右の多面体の頂がきて
稜の本数は 四角形の上は 4本 三角形の上は 3本です。
四角形の稜の中点から 双対多面体の稜が四本集まっている頂に
仰角 22.50度 (面角 67.50度の余角) で稜があります。
また 三角形の稜の中点から 双対多面体の稜が三本集まっている頂に
仰角 12.76度 (面角 77.24度の余角) で稜があります。
そして 双対多面体の面の中点の上に 準正多面体 の頂がきます。
双対多面体の面芯寸は 稜芯寸 × 基本数
1.307 × 0.934 = 1.221 です。
四角形の上の 双対頂芯寸は 多面体稜芯寸 × 多面体稜芯寸 / 多面体面芯寸
1.307 × 1.307 / 1.207 = 1.415 です。
同じように 三角形での頂芯寸は
1.307 × 1.307 / 1.274 = 1.341 です。
2012年8月27日
多面体諸量 5
多面体諸量 3 2012年8月19日 でお伝えした値に誤りがあり
ブログの変更をしています。
双対多面体面積 双対多面体体積 11 22.247967345311054163 10.853489115103684721 36 60 誤 11 30.338137289060528404 14.800212429686842801 36 60 正 2012 8/21肝に銘じて正確な情報を伝えてゆく所存です と言っていた矢先です。
急いでデータ変更と お詫びをいたします。
計算プログラムの参照テーブルの中の 多面体頂点数が 30であるべきところ 10 に
なっていたためという 初歩的ミスでした。
すべての数値を 別の計算プログラム (BASICで作成) の計算数値と比較したところ
この誤った二つの数値以外 有効桁数12桁まではすべてイコールでした。
(二つのプログラムに 共通に用いている計算ロジックの誤りは発見できませんが)
“12桁までは” とは 比較に使用した BASICプログラムの有効桁数を
誤差を考慮して 12桁に止めているからです。
一方 今回の計算をしているプログラムは 有効桁数を 20桁にしています。
多倍長電卓LM 参照 URL=http://www.vector.co.jp/soft/win95/personal/se242555.html
このブログでお伝えしている諸量の寸法は 正・準正多面体 の稜寸を 1としたときの値です。
双対多面体の寸法は稜芯寸がもとの多面体の稜芯寸と同じ値であるとして計算しています。
あらためて 肝に銘じて正確な情報を伝えてゆく所存です。
2012年8月21日
多面体諸量 4
前回お伝えし残した 双対多面体の稜寸です また数字の羅列です。
正多面体や準正多面体 の稜寸は一つの多面体には一つでしたが
双対多面体の稜寸は 複数個ある場合があります。
正多面体の双対多面体は 正多面体で
正四面体[3,3,3] ⇔ 正四面体 正八面体[3,3,3,3] ⇔ 正六面体[4,4,4]
正十二面体[5,5,5] ⇔ 正二十面体[3,3,3,3,3] となります。
以前にお伝えした双対多面体は 稜寸の数が 1つだけという特殊なものを選びました。
双稜寸1 双稜寸2 双稜寸3 01 LL= 1.0000000000000000000 02 LL= .70710678118654752440 03 LL= 1.4142135623730950488 04 LL= .61803398874989484820 05 LM= .91855865354369178682 06 LL= 3.0000000000000000000 LM= 1.8000000000000000000 07 LM= .84250916244486046725 MM= .59346535597198731050 08 LL= 1.0823922002923939688 LM= .83718607580427642316 09 LL= 1.6180339887498948482 10 LL= 2.1213203435596425732 LM= 1.5909902576697319299 11 LM= 1.0633135104400499152 12 LL= 3.4142135623730950488 LM= 2.0000000000000000000 13 LM= 1.0199882470228458983 MM= .58289953474498241442 14 LM= 1.2391601148672816338 MS= .80499198439381116988 15 LM= 2.3644524131865197592 LS= 1.9397429472460411059 MS= 1.4500488186822163018 16 LL= 1.8541019662496845446 LM= 1.6446959786840112913 17 LL= 3.6180339887498948482 LM= 2.0991063585226794765 18 LM= 2.5755459331956214849 LS= 2.1901744798065037825 MS= 1.3942870166557737040数の羅列の載せついでに 正・準正多面体 の 伝えもらしの諸量を掲載します。
これで 最後にしておきます。
面積 体積 名称
1.7320508075688772935 .11785113019775792073 01[3,3,3]
3.4641016151377545871 .47140452079103168293 02[3,3,3,3]
6.0000000000000000000 1.0000000000000000000 03[4,4,4]
8.6602540378443864676 2.1816949906249123735 04[3,3,3,3,3]
9.4641016151377545871 2.3570226039551584147 05[3,4,3,4]
12.124355652982141055 2.7105759945484321769 06[3,6,6]
19.856406460551018348 7.8894773999753902065 07[3,3,3,3,4]
21.464101615137754587 8.7140452079103168293 08[3,4,4,4]
20.645728807067603073 7.6631189606246319687 09[5,5,5]
26.784609690826527522 11.313708498984760390 10[4,6,6]
29.305982844911989541 13.835525936249404140 11[3,5,3,5]
32.434664363614895173 13.599663291074443561 12[3,8,8]
55.286744958445148944 37.616649962733362976 13[3,3,3,3,5]
59.305982844911989541 41.615323782497967065 14[3,4,5,4]
61.755172439303668108 41.798989873223330683 15[4,6,8]
72.607253034133921879 55.287730758122739236 16[5,6,6]
100.99076015310198854 85.039664559370881555 17[3,10,10]
174.29203034232392088 206.80339887498948482 18[4,6,10]
L面角 M面角 S面角
01 35.264389682754654315
02 54.735610317245345685
03 45.000000000000000000
04 69.094842552110700967
05 54.735610317245345685 70.528779365509308631
06 35.264389682754654315 74.206830951736037054
07 66.366136216794602533 76.617293856710015509
08 67.500000000000000000 77.235610317245345685
09 58.282525588538994676
10 54.735610317245345685 70.528779365509308631
11 63.434948822922010648 79.187683036428293709
12 45.000000000000000000 80.264389682754654315
13 70.842237247818090112 82.087683028016940767
14 71.565051177077989352 76.717474411461005324 82.377368140649695643
15 57.764389682754654315 67.500000000000000000 77.235610317245345685
16 69.094842552110700967 73.527789307239603390
17 58.282525588538994676 84.340106270811309681
18 65.905157447889299033 76.717474411461005324 82.377368140649695643
二面角1 二面角2 二面角3
01 LL= 70.528779365509308631
02 LL= 109.47122063449069137
03 LL= 90.000000000000000000
04 LL= 138.18968510422140193
05 LM= 125.26438968275465432
06 LL= 70.528779365509308631 LM= 109.47122063449069137
07 LM= 142.98343007350461804 MM= 153.23458771342003102
08 LL= 135.00000000000000000 LM= 144.73561031724534568
09 LL= 116.56505117707798935
10 LL= 109.47122063449069137 LM= 125.26438968275465432
11 LM= 142.62263185935030436
12 LL= 90.000000000000000000 LM= 125.26438968275465432
13 LM= 152.92992027583503088 MM= 164.17536605603388153
14 LM= 148.28252558853899468 MS= 159.09484255211070097
15 LM= 125.26438968275465432 LS= 135.00000000000000000 MS= 144.73561031724534568
16 LL= 138.18968510422140193 LM= 142.62263185935030436
17 LL= 116.56505117707798935 LM= 142.62263185935030436
18 LM= 142.62263185935030436 LS= 148.28252558853899468 MS= 159.09484255211070097
2012年8月20日
多面体諸量 3
双対多面体の諸量を掲載します。
寸法は もとの多面体の稜寸が 1のとき
複合多面体 compounds となる寸法にしています。
つまり 稜芯寸が同じです。
二面角 面芯寸 名称
70.528779365509308631 .20412414523193150818 01[3,3,3]
90.000000000000000000 .35355339059327376220 02[3,3,3,3]
109.47122063449069137 .57735026918962576451 03[4,4,4]
116.56505117707798935 .68819096023558676910 04[3,3,3,3,3]
120.00000000000000000 .75000000000000000000 05[3,4,3,4]
129.52119635864217322 .95940322360024695434 06[3,6,6]
136.30923289232420382 1.1576617909555498021 07[3,3,3,3,4]
138.11795905551232225 1.2202629537976100741 08[3,4,4,4]
138.18968510422140193 1.2228474935575285787 09[5,5,5]
143.13010235415597870 1.4230249470757706994 10[4,6,6]
144.00000000000000000 1.4635254915624211362 11[3,5,3,5]
147.35010012620952978 1.6382813268065143234 12[3,8,8]
153.17873255844969649 2.0398731549542789999 13[3,3,3,3,5]
154.12136312577632048 2.1209910195184334175 14[3,4,5,4]
155.08217961661841220 2.2097412102566332828 15[4,6,8]
156.71855372645878664 2.3771316059838161118 16[5,6,6]
160.61255220937037119 2.8852583129200411870 17[3,10,10]
164.88789190766248167 3.7366464560831424485 18[4,6,10]
L仰角 M仰角 S仰角
01 54.735610317245345685
02 35.264389682754654315
03 45.000000000000000000
04 20.905157447889299033
05 35.264389682754654315 19.471220634490691369
06 54.735610317245345685 15.793169048263962946
07 23.633863783205397467 13.382706143289984491
08 22.500000000000000000 12.764389682754654315
09 31.717474411461005324
10 35.264389682754654315 19.471220634490691369
11 26.565051177077989352 10.812316963571706291
12 45.000000000000000000 9.7356103172453456846
13 19.157762752181909888 7.9123169719830592329
14 18.434948822922010648 13.282525588538994676 7.6226318593503043571
15 32.235610317245345685 22.500000000000000000 12.764389682754654315
16 20.905157447889299033 16.472210692760396610
17 31.717474411461005324 5.6598937291886903186
18 24.094842552110700967 13.282525588538994676 7.6226318593503043571
L稜寸 M稜寸 S稜寸
01 .50000000000000000000
02 .35355339059327376220
03 .70710678118654752440
04 .30901699437494742410
05 .61237243569579452455 .30618621784789726227
06 1.5000000000000000000 .30000000000000000000
07 .54577648445886681200 .29673267798599365525
08 .54119610014619698440 .29598997565807943876
09 .80901699437494742410
10 1.0606601717798212866 .53033008588991064330
11 .76942088429381335064 .29389262614623656458
12 1.7071067811865475244 .29289321881345247560
13 .72853847965035469104 .29144976737249120721
14 .72541696649427383703 .51374314837300779674 .29124883602080337314
15 1.4270732708751722817 .93737914231134747753 .51266967637086882424
16 .92705098312484227231 .71764499555916901903
17 1.8090169943749474241 .29008936414773205235
18 1.6857166981731757817 .88982923502244570318 .50445778163332800082
Lかど角 Mかど角 Sかど角
01 60.000000000000000000
02 90.000000000000000000
03 60.000000000000000000
04 108.00000000000000000
05 70.528779365509308631 109.47122063449069137
06 33.557309761920715293 112.88538047615856941
07 80.751702088392428768 114.81207447790189281
08 81.578941881850578219 115.26317435444826534
09 60.000000000000000000
10 48.189685104221401934 83.620629791557196132
11 63.434948822922010648 116.56505117707798935
12 31.399714809919042210 117.20057038016191558
13 67.453508965514960111 118.13662275862125997
14 67.783011547435348796 86.974155491043547019 118.26867747047755717
15 37.773340083132792629 55.024696148902675288 87.201963767964532083
16 55.690639534406005565 68.618720931187988871
17 30.480324565355675308 119.03935086928864938
18 32.770278471287838669 58.237919620889530968 88.991801907822630362
L頂芯寸 M頂芯寸 S頂芯寸
01 .61237243569579452455
02 .61237243569579452455
03 1.0000000000000000000
04 .86602540378443864676
05 1.0606601717798212866 .91855865354369178682
06 1.8371173070873835736 1.1022703842524301442
07 1.3614101519264425345 1.2820358469890142117
08 1.4142135623730950488 1.3396704247226696103
09 1.5388417685876267013
10 1.8371173070873835736 1.5909902576697319299
11 1.7204774005889669228 1.5666546730064754191
12 2.4142135623730950488 1.7320508075688772935
13 2.2200006991613182111 2.1172098986276657420
14 2.2939698674519558970 2.2360679774997896964 2.1956534020612776371
15 2.6754174373368364913 2.4494897427831780982 2.3203772410170407352
16 2.5980762113533159403 2.5309268686270615215
17 3.4409548011779338455 2.9413907079821512843
18 4.1291457614135206146 3.8729833462074168852 3.8029832481815887597
面積 体積 LMS接合角
01 1.7320508075688772935 .11785113019775792073 60
02 3.0000000000000000000 .35355339059327376220 60
03 6.9282032302755091741 1.3333333333333333333 45
04 7.8859666817870040904 1.8090169943749474241 60
05 9.5459415460183915794 2.3864853865045978949 45 60
06 17.909773867919159185 5.7275649276110349476 30 60
07 19.299406563296038279 7.4473951888148613654 45 60
08 21.513454645857756671 8.7506905708484345088 45 60
09 22.672839422285121914 9.2418082864578952009 36
10 30.186917696247160902 14.318912319027587369 30 45
11 22.247967345311054163 10.853489115103684721 36 60 誤
11 30.338137289060528404 14.800212429686842801 36 60 正 2012 8/21
12 42.691767495934186821 23.313708498984760390 22.5 60
13 55.280530923261226254 37.588423673993486442 36 60
14 59.767395102644803054 42.255369424239875108 36 45 60
15 67.424848155089284364 49.663821854532241004 22.5 30 45
16 75.565544704433850714 59.876414880097563514 30 36
17 115.56968556618976742 111.14946533380144110 18 60
18 183.19554518150396045 228.17899489089532558 18 30 45
2012年8月19日
多面体諸量 2
前回の続きで 多面体諸量の 二面角についてお伝えします。
多面体の面と面とが接する稜にできる角度のことですが
さいころの形をした正六面体 [4,4,4] の二面角は 90度だといえばお判りでしょう。
今お伝えしている 正多面体や準正多面体 の製作過程には必要としません。
できた完成品を見て 認識を深めるだけです。
ただ 複合多面体などでお伝えした 双対多面体の製作には必要な数値です。
上の画像をクリックすると エクセル画面が拡大されて見えます。
後日投稿のリメイク版もあります。
[ 3,4,5,4 ] に限らず
プラトン多面体や アルキメデス多面体 など
18種類ある値の計算ができます。
1 行目 B 列 → 稜芯寸 4 行目 A 列 → 角数 4 行目 B 列 → 多角形の辺芯寸 4 行目 C 列 → 面角 4 行目 D 列 → 面芯寸 4 行目 E 列 → 双対仰角 4 行目 F 列 → 双対稜寸 5 行目 B 列 → =0.5/TAN(PI()/A5) 5 行目 C 列 → =DEGREES(ACOS(B5/$B$2)) 5 行目 D 列 → =SQRT($B$2^2-B5^2) 5 行目 E 列 → =90-C5 5 行目 F 列 → =$B$2/D5*B5 5 行目 B 列 から F 列 までを選択し セルの右下にポインタを合わせ 「＋」を下方( 7行目まで ) にドラッグする[オートフィル]を行います。この画面の計算は [ 3,4,5,4 ] の計算です。
この多面体の二面角は 三角形と四角形の二面角
82.3773681406496＋76.7174744114609 = 159.094842552110 と
四角形と五角形の二面角
76.7174744114609＋71.5650511770778 = 148.282525588539 の二つです。
五角形と三角形の二面角はありません。
ある書籍には この幻の二面角の数値 153.942419317727 を
153°56′33″と表記して諸量に載せてあるのがありました。
私も人のことは言っておられません 肝に銘じて正確な情報を伝えてゆく所存です。
左は 私の初期の作品で 接着剤が劣化していて 一部の部品が剥がれていました。
高さ約 75mm 6×6 の竹製で 斜方立方8面体 [3,4,4,4] です。
右はその双対多面体の凧形24面体です これも古い作品です。
4×4のバルサ材での作品ですが 歪みもみられず まずまずの状態です。
次回は この[3,4,4,4]の双対形である凧形24面体についてお伝えしようと思っています。
2012年8月18日
多面体諸量
正多面体 準正多面体 の諸量を表示します。
2012年7月9日のブログで エクセルでの 数値の求め方をお伝えしましたが
そこで入力できる数値より少し精度の高い値を 載せておきます。
基本数とは 頂芯寸を 1 としたときの 稜芯寸の値です。
エクセルの画面に この値が入れば 各接合角の合計が 360度になります。
入力値との確認等に ご利用ください。
パズル気分で 入力ができます。
ここで “芯”という用語を用いていますが
立体上の 中芯点という意味で使用しています。
現代の高等幾何学での 用語とは意味が違いますが 問題はないでしょう。
また 平面上では “心”という用語を 中心点という意味で用いています。
稜と辺 頂と”かど” も使い分けを意図しています。
基本数 仰角 名称
.57735026918962576451 54.735610317245345685 01[3,3,3]
.70710678118654752440 45.000000000000000000 02[3,3,3,3]
.81649658092772603273 35.264389682754654315 03[4,4,4]
.85065080835203993218 31.717474411461005324 04[3,3,3,3,3]
.86602540378443864676 30.000000000000000000 05[3,4,3,4]
.90453403373329086794 25.239401820678913392 06[3,6,6]
.92819137798557160941 21.845383553837898091 07[3,3,3,3,4]
.93394883109446475958 20.941020472243838873 08[3,4,4,4]
.93417235896271569645 20.905157447889299033 09[5,5,5]
.94868329805051379960 18.434948822922010648 10[4,6,6]
.95105651629515357212 18.000000000000000000 11[3,5,3,5]
.95968298226066728914 16.324949936895235112 12[3,8,8]
.97273285056559586532 13.410633720775151757 13[3,3,3,3,5]
.97460776237817045237 12.939318437111839760 14[3,4,5,4]
.97645097624651324115 12.458910191690793901 15[4,6,8]
.97943208548641418658 11.640723136770606678 16[5,6,6]
.98572191928130191461 9.6937238953148144071 17[3,10,10]
.99131668954105939137 7.5560540461687591650 18[4,6,10]
頂芯寸 稜芯寸 名称
.61237243569579452455 .35355339059327376220 01[3,3,3]
.70710678118654752440 .50000000000000000000 02[3,3,3,3]
.86602540378443864676 .70710678118654752440 03[4,4,4]
.95105651629515357212 .80901699437494742410 04[3,3,3,3,3]
1.0000000000000000000 .86602540378443864676 05[3,4,3,4]
1.1726039399558573886 1.0606601717798212866 06[3,6,6]
1.3437133737446017013 1.2472231679936432518 07[3,3,3,3,4]
1.3989663259659067020 1.3065629648763765279 08[3,4,4,4]
1.4012585384440735447 1.3090169943749474241 09[5,5,5]
1.5811388300841896660 1.5000000000000000000 10[4,6,6]
1.6180339887498948482 1.5388417685876267013 11[3,5,3,5]
1.7788236456639244509 1.7071067811865475244 12[3,8,8]
2.1558373751156397018 2.0970538352520879924 13[3,3,3,3,5]
2.2329505094156900495 2.1762508994828215111 14[3,4,5,4]
2.3176109128927665138 2.2630334384537146236 15[4,6,8]
2.4780186590676155376 2.4270509831248422723 16[5,6,6]
2.9694490158633984670 2.9270509831248422723 17[3,10,10]
3.8023944998512935848 3.7693771279217166027 18[4,6,10]
L接合角 M接合角 S接合角
01 60.000000000000000000
02 45.000000000000000000
03 60.000000000000000000
04 36.000000000000000000
05 54.735610317245345685 35.264389682754654315
06 73.221345119039642354 33.557309761920715293
07 49.624148955803785616 32.593962761049053596
08 49.210529059074710890 32.368412822775867329
09 60.000000000000000000
10 65.905157447889299033 48.189685104221401934
11 58.282525588538994676 31.717474411461005324
12 74.300142595040478895 31.399714809919042210
13 56.273245517242519944 30.931688620689370014
14 56.108494226282325602 46.512922254478226490 30.865661264761221417
15 71.113329958433603686 62.487651925548662356 46.399018116017733958
16 62.154680232796997218 55.690639534406005565
17 74.759837717322162346 30.480324565355675308
18 73.614860764356080665 60.881040189555234516 45.504099046088684819
S面芯寸 M面芯寸 L面芯寸
01 .20412414523193150818
02 .40824829046386301637
03 .50000000000000000000
04 .75576131407617073048
05 .81649658092772603273 .70710678118654752440
06 1.0206207261596575409 .61237243569579452455
07 1.2133558000218923103 1.1426135089259620935
08 1.2742736942483016631 1.2071067811865475244
09 1.1135163644116067352
10 1.4142135623730950488 1.2247448713915890491
11 1.5115226281523414610 1.3763819204711735382
12 1.6825219847121646795 1.2071067811865475244
13 2.0770896597432085994 1.9809159472818407390
14 2.1570198525202442752 2.1180339887498948482 2.0645728807067603073
15 2.2071067811865475244 2.0907702751760276959 1.9142135623730950488
16 2.3274384367663271103 2.2672839422285121914
17 2.9127811665964150056 2.4898982848827802734
18 3.7360679774997896964 3.6685424806725857361 3.4409548011779338455
2012年8月16日
sashimono [ 3,4,5,4 ] 10 Rhombicosidodecahedron
[ 3,4,5,4 ] の二種類の部品製作が終わりました。
三角用と四角用の接合面をもつ部品を三つ合わせて三角形の稜を 20個。
四角用と五角用の接合面をもつ部品を五つ合わせて五角形の稜を 12個 作りました。
接着剤は透明タイプの合成ゴム系です。
チューブから接着剤を出す場合 取り出し口からほんの少し出る程度
表面張力で球状になりますが 半球にもならない程度にして
楊枝で接着剤をすくい 薄く接着面の両方に塗って接合しています。
溶剤の揮発成分のことも 気にならないで済むでしょう。
組み立てが完了すれば 左の完成品と同じ大きさになります。
sashimono という言葉を英語版の Wikipedia では
戦国時代の兵が戦闘で用いた旗指物として説明がなされています。
本来なら hata sashimono という項目で説明すべきだと思います。
我々が普通に “指物” と言えば
伝統工芸の 木工品のことですが 説明にはありません。
一応完成しましたが 指物とはいえない作品になってしまいました。
左側の作品は 約10年ほど前に作った プロトタイプです。
作る目的が 自分のためではなく 画像に載せて説明するためのサンプルであり
完成を急いだ と 言い訳を言っておきます。
まず第一に言えることは
四角をつくる接合面製作のクレィドル cradle の精度が悪かったということです。
2012年8月12日
sashimono [ 3,4,5,4 ] 9 Rhombicosidodecahedron
久しぶりの投稿です。
今日のブログの表題を
斜方20･12面体 [ 3,4,5,4 ] とせず sashimono [ 3,4,5,4 ] としましたのは
私が多面体を作るときにいつも意識している
“指物” という言葉を伝えたかったからです。
指物は 日本の “伝統的な木工芸” の職人技を表す造作物の一つです。
今ある手持ちの道具で 表せる可能性を強く追求し
妥協を避けながら できるだけ速やかに できるだけ正確に作ろう
という職人意識が強く感じられ 大変好きな言葉です。
“指物” とせず “sashimono” としたのは
日本においてだけでなく 広く通用する意味のある言葉だと思っているからです。
私もそのような作品を作りたいと 願いをこめて sashimono と表記しました。
まだ[ 3,4,5,4 ]は 部品の製作中です
その作業の中で気づいたことをお伝えします。
クレィドル cradle 製作の提案として
それぞれ左右対称の 三角面用 四角面用 そして五角面用と三つ作ることを
お伝えしましたが それだけの cradle では
私自身の実際の製作作業では 混乱か生じました。
四角用と五角用の接合面をもつ部品製作で
右が四角 左が五角で
その部品を 180度回転させると 左は四角で右は五角なのですが
単純反復作業では 頭の中が空っぽになってしまい ミスが多発しました。
(これは 私個人の能力や性格の問題かもしれませんが)
写真に写っている作業台の 左上の cradle は
左五角 右四角 下は 左四角 右五角です。
一つの cradle で 部品の一つの端を加工し
他の端をもう一つの cradle で加工するという作業に変更をしました。
しかし 両端を一つの cradle で加工してしまうというミスもあり
色分けか 番号づけして
二種類使用が必要と感覚的に判るようにしようかと思っています。
それらの cradle の右にあるのは ルーペ付きキーホゥルダーの ルーペです。
接眼レンズは直径 10mm で 10mm の対象物が 視野に入ります。
わりと値のはる 光学機器とよぶべきルーペと比較して
遜色なしというより 小額で手にしたこちらの方が気に入っています。
作業台右の二つの cradle は 三角面と四角面がセットになった部品の製作用です。
画面下のグラフ用紙は 仰角(12.9度) を表わすのに
筆記具でなく カッターナイフを用いて表示したことにより 分割されています。
これは一種の “けがき” です。
けがきは 金属加工や 指物つくりで 線引きや 位置決めに使われる技法で
シャープな線が引けます。
“けがき針” という 先の尖った金属棒を用います。
私は用紙に線をプロットする場合にも カッターナイフを用いることがあり
より鋭い線が得られるからです。
画面左上は 完成した 60個の 四角と三角の接合面がセットの部品が袋に入っています。
画面右上は 完成30 未完成30 のもう一種類の部品です。
5×5 の 稜寸 16mm のプラ棒です。
左下の袋に入った部品は稜寸 16mm で 5×5 のラフカットのバルサ材 120個です。
2012年8月10日
斜方20･12面体 [ 3,4,5,4 ] 8 Rhombicosidodecahedron
前回お伝えした画像の 左右反転前の左きき用の治具ですが
この治具でも 右用に使えます。
ストッパーに当てて定寸にカットする部材部分をフリーにして
のこぎりの左側のカットすると余りになる部分を固定して作業するのです。
次の作業として 余りの角棒のカットされた面をドレサーで整形し
その整形面を 治具のストッパーに当てて 同じ作業を続ける場合
この治具では 角棒を上のストッパーのない溝に 向きを変えることなく置いて
ドレサーで整形できるからです。
なぜこのような事を くどくどと説明しているかといいますと
[ 3,4,5,4 ] を完成させるのに必要なこの治具でつくる部品点数は 1種類のみで 120個です。
1mm の数分の一の精度 (特に部品寸法が 20mmほどか それ以下の場合)で
継続して “もくもくと” 加工していく必要があります。
私は今回 高さ約 70mm 部品寸法 約 16mm の [ 3,4,5,4 ] を作ろうと思っています。
以前にもお伝えしたことがありますが
製作する部品の一つでも 精度の悪いものが混じってしまうと 努力の割りに不本意な作品が
できてしまう場合があります。
少しでも作業性を上げて 良品を作り続けられる環境が必要だからです。
2012年8月2日
斜方20･12面体 [ 3,4,5,4 ] 7 Rhombicosidodecahedron
[ 3,4,5,4 ] の製作部品を 仰角(12.9度) の余角の 77.1度でカットする治具です。
私は左ききですが この写真は右用です (左きき用の画像を左右反転しています)。
今回は 5×5 の角棒で製作するつもりですが 説明のため 10×10 用です。
三角棒でできた溝に置いている木片を左から説明します。
左端に乗った部品は
その右にある部品 (テープで固定しています) が左方向にずれないよう溝に接着しています。
テープで固定した部品は 取り外しして寸法変更が可能です。
77.1度に右の面は整形しています これをストッパーとして 77.1度に整形した角棒を当て
定寸で 77.1度の角度でカットします。
これから切断加工をしようとする角材の ストッパーにあてる面は
のこぎりでカットした荒い表面のままか ドレサーで整形後の面かが考えられますが
私は ドレサーで整形後にカットする方法をとっています。
両面がラフなまま 必要個数カット後に 両面整形する部品より
片面のみ整形する部品のほうが 寸法誤差のばらつきが少なく
歩留まりや 作業性が 優れていると 私は思います。
用いる道具や 作業者の 技量 性格や 好みによっても違ってくるでしょう。
私は治具やクレィドルは 消耗品だと思っています。
だから その都度作っていますし 形状も同じでばありません。
ある作品を作るために作った治具やクレィドルは いつ再度利用するかわかりません。
100パーセント完全にできたとは 到底思えませんし
時間がたてば 変形 ゆがみも発生します。
今の自分は 過去よりアイデアも増えているだろうし 技量もアップしているはずです。
2012年7月31日
斜方20･12面体 [ 3,4,5,4 ] 6 Rhombicosidodecahedron
斜方20･12面体 [ 3,4,5,4 ] 製作に必要なクレィドルの作りかたをお伝えします。
左に表示の 斜線を引いた長方形の木片は 15×20×70 のバルサ材です。
15mm巾で 12.9度の傾斜で角材を 必要な接合角で加工するクレィドルの部品です。
20×70 の面を上にして 70mmの方向の部分をグラフの斜線に合わせ
横方向の直線に平行に 20×70 の面に斜線を引きます。
もう一つの20×70 の面に斜めに線を引く作業方法は
70mmの方向の部分を 横方向の直線に合わせる方法もありますが
参照する斜線は 1本しかなく 位置あわせ作業に スムーズさに欠けます。
バルサ材を斜線に沿ってカットし ラフな面を上の治具で 12.9度の傾斜に整形します。
右に表示のグラフ用紙には 底辺 104 対辺 174 で 角度 59.1度 ( 90度-30.9度)の線を
左右から引き 両線の交わるところは 30.9度＋30.9度 となっていて
[ 3,4,5,4 ]の 三角部分の接合面をつくる クレィドルのガイドの部品です。
寸法は 6×30×90 で 切断部を合わせて 接合面を 30.9度＋30.9度にします。
画面まん中が 12.9度の仰角で 製作部品の接合面を 30.9度にするクレィドルで
先端の整形はまだですが 斜面に断面が直角二等辺三角形のプラ棒を貼っています。
プラ棒の断面寸法ですが 斜辺が約 7mm 左右の辺が 5mm です。
今まで 製作見本として 作ってきました模型は 10×10 のバルサ材だったので
かなりのかさ張りがあり 今後は 5×5 のプラ棒で見本を作ろうかなと思っています。
右側の上が 底辺 195 対辺 131 で 角度 33.9度 ( 90度-56.1度)の線を
左右から引き 両線の交わるところは 56.1度＋56.1度 となっていて
5角形の接合面を作るクレィドルの製作途中です。
右側の下が 底辺 175 対辺 166 で 角度 43.5度 ( 90度-46.5度)の線を
左右から引き 両線の交わるところは 46.5度＋46.5度 となっていて
4角形の接合面を作るクレィドルの製作途中です。
左側の治具は 仰角(12.9度) の余角の 77.1度で製作部品をカットするために
台の板を 12.9度傾け 三角棒を垂直方向に接着しています。
溝が 2本あるのは ストッパーのないフリーな溝も必要なためです。
2012年7月27日
多面体製作道具2
多面体製作において あると便利と思える治具の製作プロセスについて お伝えします。
右の三角定規の下にある 6×120×120 の板材は 90度の加工面を作るための治具です。
上に角材 (25×25×150) を置いているのは
三角定規を板材の直線と正確に一致させるためです。
目視で定規をあてると知らぬ間にずれたり 精度が悪くなったりします。
左の縦方向に 5×15×120 の板材を定規にあてて接着します。
定規に合わせて書いた直線にそって接着するより精度が高くなります。
接着剤は木工用ボンドを お勧めします 接着後に位置修正が可能です。
両面テープや 合成ゴム系接着剤での接合は 微調整が困難です。
左側は斜方20･12面体 [ 3,4,5,4 ] の仰角 (12.9度) のクレィドルを作るための治具です。
板材 (6×150×180) を グラフ用紙にあわせ角材 (15×30×200) を 対辺 51 底辺 222で
グラフ用紙に表示した斜線方向に置き 両面テープで接着します。
ドレサーが接する クレィドルや治具の直線部分は
すべて購入した材料のオリジナルな 加工面を使っています。
購入後の加工でできた直線は 精度が低く 極力使用を避けるべきです。
繰り返しですが ここでお伝えしている治具の数値は 手もちの材料をもとに決定したもので
限定的なものではありません
2012年7月26日
多面体製作道具
あらためて 多面体製作に必要なものを 説明します。
画面の中ほどにある木製の盆は 加工作業中に発生した木の屑の飛散を防ぐためのものです。
縦 235mm 横 355mm 深さ 14mm で 100円で買ったものです。
その右にある 14×50×27 の木材 2本を下にして
6×15×27 の板を両面テープでこの盆に固定します。
盆の裏には すべり止めマットを貼っています。
ほとんどの 製作加工をこの板の台の上でおこなっています。
木の屑の発生 特に細かい木の粉 の発生に対し 注意することが大切です。
防塵マスクを付ける必要がある場合も考えられます まめな クリーニングや掃除が必要です。
盆の上にある 25×25×95 の木材片に 平目の平面ドレサーを貼っています。
このドレサーの巾は 20mmで 5mmの隙間ができます。
これは 切削する材料を固定し定まった形にするガイドの 形状を損ねないためです。
ガイド ( 6mmの厚みに統一) の一部を切削加工時点で
加工している部品と一緒に削ることが必要な場合もありますので 5mmの隙間にしています。
直角を表す形状をしたものがその下にありますが スコヤという道具です。
直角を判定するためだけの道具といえるもので 絶対に必要かといえば NOです。
画面左に三角定規を載せていますが これで間に合います でも
直角の確認が多くの作業にある木工加工において 象徴的な道具です。
精密な木工加工を楽しむ者としては 手にしていたいものです。
三角定規は大きめのを載せています。
グラフ用紙での角度決定か゛主流ですが
90度 45度 30度 60度 の表示には こちらのほうが優れています。
のこぎりは 切断面がきれいに仕上がる 細密加工用です。
ここでお伝えした 材料やその寸法は
たまたま私の手もとにある材料にあわせて決定したもので
あくまでも 参考としてお伝えしています。
2012年7月24日
斜方20･12面体 [ 3,4,5,4 ] 5 Rhombicosidodecahedron
前回お伝えした 画像内容に不備がありましたので 訂正した画像を掲載します。
画像をクリックすれば より大きな画面になります。
左上の 4角形の接合角 ↑166(対辺) を ↑166(底辺)
←175(底辺) を ←175(対辺) に。
左下の 5角形の接合角 ↓131(対辺) を ↓131(底辺)
←195(底辺) を ←195(対辺) に。
右下の 46.513°の表示位置 が誤っていました ご迷惑をお許しください。
製作に必要な角度の参考にすべき基本データを A4のグラフ用紙で表示することを
このブログではお勧めしています。
分度器よりも A4のグラフ用紙のほうが
今 手ぢかにあるものの中で最も精度が高く表示でき
扱いやすいものとして はるかに優れています。
数値計算は 以前お伝えした エクセルでおこなうことを説明しましたが
A4 のグラフ用紙での表示は
対辺のマクシマムが 180 であり 底辺のマクシマムが 250 のため
45度以上の角度は 90度から 求める角度をマイナスし 余角の数値で計算し
分数の分子が 分母より小になるようにする必要があります。
また 分子の値も 180以下の計算結果を読み取る必要があり
” =SMALL(D2:D81;1) ←1行目 E 列 ” の (D2:D81;1) の 1 の値を (D2:D81;2)
など 数値を上げてゆくことが必要になる場合も起こります。
かなり煩雑な作業のように思えますが。
確かに 小数点以下の角度まで意識することは 日常生活ではほとんどありませんし
余角とは 90度からある角度(90度より小) を引いた値である
という概念もあまり必要ありません。
しかし 何かをしたいがそれをするのには必要だとなれば
理解しようとする気も湧き 楽しいものです。
いずれ BASIC での計算も お伝えしようと思っています。
2012年7月21日
斜方20･12面体 [ 3,4,5,4 ]4 Rhombicosidodecahedron
斜方20･12面体 [ 3,4,5,4 ]の 製作用図です。
[ 3,4,5,4 ]とある通り 一つの頂に正多角形が 3,4,5,4 と集まっています。
このブログでお伝えしている 多面体模型は レオナルドスタイル(Leonardo-style) ですが
レオナルド ダ ヴィンチ(Leonardo da Vinci) の絵に見えるスタイルは “透けた多角形” の立体として面角を残し 面の形状で表現しようとしてると私には思えます。
私は “太さのある線” の立体として 多面体を 捉えようとしています。
また 当時 どれくらい三角関数の恩恵があったのか 調べてみたいと思っています。
[ 3,4,5,4 ]は 準正多面体 なので 仰角は一種類 ( 12.939°余角=77.061°)です。
部品の稜線を縦方向に向けると
片方の上下の接合角が四角形をつくる接合角 ( 46.513°余角=43.487°)
もう片方の上下が 三角形をつくる接合角 ( 30.866°) の部品が 60個と
片方の上下の接合角が四角形をつくる接合角 ( 46.513°余角=43.487°)
もう片方の上下が 五角形をつくる接合角 ( 56.108°余角=33.892°) の部品 60個必要です。
上記の部品を作るためのクレィドルは
仰角 12.939°に余角の 77.061°でカットした面を垂直にし加工する 三種類があります。
左右 三角形用 左右 四角形用 左右 五角形用 です。
くれぐれも注意してください。
部品の稜線を縦方向に向けた場合 上下の切削形状が 面対象になるようにです。
接合方法をお伝えします あくまでも一つの方法です。
三角形を作る切削面のある部品で 三角形を 20個作り
五角形を作る切削面のある部品で 五角形を 12個作り
完成した多面体を参考( Wikipedia 等でも 色々な情報が得られます ) に
五角形と三角形を接合してゆきます。
アバウトな説明ですが 作業はこれで進むと思います。
2012年7月16日
斜方20･12面体 [ 3,4,5,4 ]3 Rhombicosidodecahedron
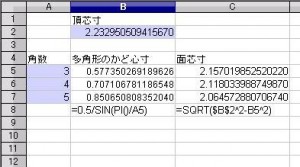
斜方20･12面体 [ 3,4,5,4 ] の 面芯寸の計算画面です。
(後日 投稿のリメイク版もあります。)
[ 3,4,5,4 ] に限らず
プラトン多面体や アルキメデス多面体 など
18種類ある値の計算ができます。
頂芯寸 2.23295050941567 角数 3 4 5 を手入力し
=0.5/SIN(PI()/A5) を 5行 B列に
=SQRT($B$2^2-B5^2) を 5行 C列に 入れ 7行まで オートフィルして下さい。
完成品の三角面を底にして置いて 多面体の高さが 7cm になった場合 稜寸は
7 × 1 / ( 2.157×2 ) = 1.623 です。
2012年7月14日
斜方20･12面体 [ 3,4,5,4 ]2 Rhombicosidodecahedron
14[3,4,5,4] Excel ポーカーの確率 多面体 諸量
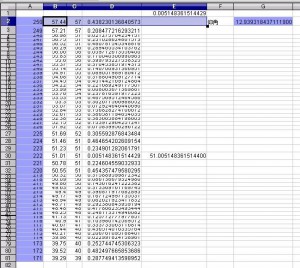
今度は 角度をグラフ用紙に表示するための整数比換算のエクセル画面です。
計算式は以下です。 後日投稿のリメイク版もあります。
[ 3,4,5,4 ] に限らず
プラトン多面体や アルキメデス多面体 など
18種類ある値の計算ができます。
1行目 E 列 =SMALL(D2:D81,1) 2行目 B 列 =TAN(RADIANS($G$2))*A2 2行目 C 列 =ROUND( TAN(RADIANS($G$2))*A2,0) 2行目 D 列 =ABS(B2-C2) 2行目 E 列 =IF(D2=$E$1,B2," ") 2行目 B 列から E列までを選択し セルの右下にポインタを合わせ 「＋」を下方(81行まで)にドラッグする[オートフィル]を行います。 A列の 2行目に 250 A列の 3行目に 249 を入れ 250と249を選択し 81行目までオートフィルします。 *2015年3月20日変更2行目 G列に 12.9393184371119 を入れると
上に掲載の画面と同じ表示結果になります。
この数字は 斜方20･12面体 [ 3,4,5,4 ]の製作部品の仰角で
A列の250 から 171の範囲での計算で
1行目 E列の数値が 最も近似の角度表示をする整数比の 誤差です。
30行目 E列の数値の 222 と 51 がその答えだということです。
A列の数字を251行まで入れて 1までで計算すると
74 対 17.001 が一番誤差が少なく 次は 148 対 34.003 で
三番目に 222 対 51.005 なのですが
エクセルで 関数計算的な数値処理をする場合 煩雑なこともありますが
関数電卓で 数値処理をするより遥かに便利でした (多面体関連についてですが)。
今は フリーウェアーソフトの 十進BASIC を使っています。
http://hp.vector.co.jp/authors/VA008683/ を参照
このソフトがなかったら 多面体製作が趣味になっていなかったかも知れません。
そのほか ポーカーの役の確率計算を 順列や組み合わせを用いた論理計算ではなく
全数チェックで しかも短時間で調べることもできました。
2012年7月12日
