RECENT POSTS
09[5,5,5] Compounds 多面体 未分類
09[5,5,5] のカテゴリーで 既にお伝えしている内容ですが
説明を変えて もう少し詳しく 話を進めてゆこうと思っています。
下画像の 左が それで
正十二面体とか Dodecahedron と呼ばれている 正多面体の一つです。
その横が 正二十面体 そして最後に それらの複合した多面体です。
正五角形 が 12個 組み合わされて できています。
正五角形の 辺と辺が接しているところを 稜とし
かど と かど とが接しているところを 頂 として
立体の 中心を 中芯 という用語を 用いて説明します。

以下に 諸量を記します。特に ことわり の無いかぎり 稜寸は1としての値です。
09 [5,5,5] Dodecahedron 正12面体
09 1.0000000000000000000 [5,5,5]稜寸
09 .93417235896271569645 [5,5,5]基本数
09 20.905157447889299033 [5,5,5]仰 角( 089/233 )
09 60.000000000000000000 [5,5,5]接合角( 194/112 )
09 58.282525588538994676 [5,5,5]片面角( 233/144 )
09 1.4012585384440735447 [5,5,5]頂芯寸( 220/157 )
09 1.3090169943749474241 [5,5,5]稜芯寸( 233/178 )
09 1.1135163644116067352 [5,5,5]面芯寸( 157/141 )
09 116.56505117707798935 [5,5,5]ニ面角
09 20.645728807067603073 [5,5,5]面積
09 7.6631189606246319687 [5,5,5]体積
09 [5,5,5] 稜部品 必要個数 30
20桁の値で表示しています。
エクセルは 15桁 関数電卓は 10桁ぐらいですが
有効桁数を確認する場合に必要なので この桁にしています。
別の理由として
他人の成果を そのまま用いているのでは無いと
少しは理解してもらえるかな との思いもありました。
今日は これからの ブログ製作の抱負 や 意気込みを
述べたにとどまってしまいました。
不定期に 思いつくまま 補足説明をしてゆこうと思っています。
2015年10月18日
11[3,5,3,5] 多面体 製作道具
[3,5,3,5] を 角棒の正三角形のみで作る方法を お伝えします。
[3,5,3,5] の製作説明シリーズは 今回までにしようと思ってます。
三角形や治具の作り方は
前回までの説明で 理解されているものとします。
角材で作った 正三角形 20個を かどとかどとを接合しながら
正五角形を 三角形の辺で作ると [3,5,3,5] の立体ができます。
ただこれは 理屈上のことで
実際の作業では 無重力状態でもないかぎり
位置固定の補助構造物なしに
それぞれの形状を保持しながらの 立体製作はできません。
そこで 最低でも二個の 三角形を かどとかど とを接合した
ユニットが四つ必要となります。これを 2型ユニットとします。
これは 前回も説明している 五角形と五角形を接合する治具の
三角形が向かい合った形状部分で行えます。
その作業でできた 2型ユニットに もう一つ 三角形を接合した
3型ユニットを四つ 作ります。
上に説明した 治具に2型ユニットの 三角を一つずらせて乗せ
それに三角を接合します。下の画像のような方法も考えられます。
2型ユニットの支えで 三角形と2型ユニットを接合します。
そして もう一つの 2型ユニットで 開き具合を調整します。
この 2型ユニット四つ 3型ユニット四つ を構築材料として
かど と かど とを接合しながら 正五角形を 三角形の辺で作ってゆく
という ルールに従えば パズル気分で 立体が完成します。

あと説明すべきことは 三角形の接合面の整形です。
アークサイン ( 三角形の面芯寸 / 頂芯寸 ) で
その角度が求まります。
arcsin ( 1.51152 / 1.61803 ) = 69.0950° となります。
69.0950° を直角を挟む 二辺の比として考えると
233/089 ( 69.0944°) が近似値です。
288/110 ( 69.0959°) が次に近い値です。
この値をもとに 傾斜をつくり 治具の製作をすればよいのですが
簡易な方法を お伝えします。
上画像の 左下のように
五角形での[3,5,3,5] を作るための治具と同じ方法で
三角形の かどと かどを合わせ
その間を 五角形の二辺だけで支える治具を作ります。
強度を高めるために しっかりと固化させます。
これだけでは 加工作業の面積が少ないため 長方形の板を貼ったり
ガイドをつけたりしています。
2015年10月13日
11[3,5,3,5] 多面体 製作道具
下の画像で 部品製作用治具の作り方を 前回に続いて説明します。
このブログの中の 製作道具のカテゴリーの内容と
重複するのもありますが くどくどと説明してきたついでに お伝えします。
70 × 30 × 3 mm の木片が 4 個写っています。
このくらいの寸法の木片が 治具の試作や 製作の補助する材料として
重宝することがあり事前に 複数個すでに作ってあったものを使用しています。
A4 の用紙に 用紙の右下かど から 245mm 左 178㎜ 上 の点を結んだ線と
用紙を縦方向に二つ折りにした線があります。
その線で 54° の角度の接合面を持つ 部品をつくる治具の角度決定をしています。
その定まった線に沿って 角棒を木片に接着させているところです。
さし( ruler ) と 三角定規( triangle ) で直線を決めているのは
小さい範囲のなかで 直線の方向を決定するより 誤差が少なくなるからです。

製作途中の 治具の左に完成した治具があります。
寸法決定のための ストッパーが接着されています。
その 位置決めは
マザー( mother) となる 部品をのせて決定します。
この治具の左横に この治具で整形した接合面で
二本の角棒を接合した 角度整形ガイドがあります。
このガイドの左右の寸法は
これから作ろうとしている部品の寸法に合わせています。
それそれの端は 直角に整形しています。
のこぎりで 切りっぱなしでもいい部分でも 面を整えるようにしています。
雑な部分の少ない よりシンメトリーな 治具で モノづくりをしていると
誤差や 異常に気づくのが より容易になると 思っています。
その 面を整えるためものを 板の側面に直角な棒を貼って作っています。
スコヤ ( Machinist square ) で位置決めをしています。
三角定規でそれを行うと 板の側面の直線に 目視で合わせます。
線と線か接しているのを確認するのとでは 正確性が異なります。
さしがね ( Steel square ) でも 近い作業ができますが。
少し 劣ります。
これは 私が実感した 木工作業一般でのことで
ここでの作業の 誤差やバラツキの許容範囲は あまり気にしなくてもいいです。
続いて 下の画像の説明です。

右上の治具で 五角形のユニットを 31.72° 傾けその かど を
垂直に 切削加工します。 粗目のサンドペーパーを貼った ドレサーで。
下にある 同じ形状の へこんだ面を上向きにした治具で 二つの五角形を接合します。
五角形を二つ接合したユニットを 六つつくります。
この形状の治具は 一つ作ればよく 撮影のために二個作っただけです。
接着剤は ここまでの作業では すべて木工用ボンドを 私は使っています。
完全に 固化した後に 次の作業に進みます。
後の作業は 思う以上に簡単だと思います。接着剤は 合成ゴム系を使っています。
二つつながった五角形を 三つつなげると 半円球状になり それらを合わせると完成です。
まったく 今まで木工もしたことのない人をも 想定しながら話を進めてきましたが
くどさだけだった 言われるかもしれません。
一人でも多く このような木工に 親しんでもらえる人が増えることを望んでいます。
2015年10月8日
11[3,5,3,5] 多面体 製作道具
今回も [3,5,3,5] の話題をつづけます。下の画像の説明をします。
左上がスコヤ ( Machinist square ) 右下が 部品製作用治具。
右中ほどのは 二つの五角形を かど で接合したユニットで
裏から見て へこんで見える状態。
その左が ユニットを 上から見て 丸みを帯びて見える状態。
その斜め左下が治具です。二種類の多角形をつなぐため
こちらの面つまり立体形状の裏側から
透明なテープを貼った状態。形状が固化しておらず 不安定。
両面テープをつかっています。接着力の違いの種類が多く
必要でない部分にまで ねばつき があっても 活用しています。
その斜め左下も治具で 上から見て 丸みを帯びて見える状態で
形状が固化しており 安定。
立体的形状の外側が見える状態で 内側の多角形の
辺と辺は ぴったりと接しており こちら側からは 開いて見えます。
その隙間を ボンドと楊枝で埋め 固化させています。
この治具の斜面に 完全に固化した五角形形状ユニットを置き
五つある各かどを 58.28° の角度で整形します。
この治具の面の傾斜は 正確につくると 31.72° になり
五角形ユニットをその面に乗せて かど を 90° 直角に面整形をすれば
58.28° の角度の接合面になります。

説明のつづきは 次回に。
2015年10月5日
11[3,5,3,5] 多面体 製作道具
今回も [3,5,3,5] の話題をつづけます。下の画像の説明をします。
右上 にあるのが アルミ製の三角定規。
その左が さしがね ( Steel square ) 。
その左は 私が ドレサー ( Dresser ) と呼んでいるものです。
形を整え 綺麗にする の意で この用語をもちいています。
金属製の やすり ( 中目 ) が角材に貼られています。
その左下は 同じ寸法の角材に 紙やすり ( 粗目 ) が貼られています。
その下の 二つの治具は 角棒でつくる五角形の 部品の切断・整形をするもので
同じ加工作業をしますが 右が 簡略した治具です。

それらの 右横に 五角形二つを かどを向かい合わせた塊が 四つあります。
上二つが 治具で 五角形と五角形の間に 三角形と三角形があります。
そのなかの右側の治具に 五角形になったユニットを乗せています。
左のが その治具の製作途中で V 字型の隙間があり 楊枝を埋めます。
この治具で 下に二つある形状のユニットと同じものをつくります。
画像右中ほどにあるユニットもそれらで 計六個必要です。
その下が 完成した多面体です。
あとは 70mm × 140mm の白い板の上に
15mm 高く 70mm × 70mm の板が貼られている治具です。
この治具に乗せて 板や角材を切断します。
今は スコヤ ( Machinist square ) が乗っています。
白い板は厚み 3mm のプラスチックの板で 簡易まな板として売られています。
上に説明した ドレサーの下面にも貼っています。
もう少し説明が必要ですが 次回にします。
2015年10月4日
11[3,5,3,5] 多面体 製作道具
[3,5,3,5] の話題をつづけます。
角棒で 正三角形をつくるための角度を表す シンプルな図をA4用紙で描きます。
下の画像のように。
長い巾の方向に 紙のかどから 265mm のところに 印しをつけ。
短い巾の方向に 紙のかどから 153mm のところに 印しをつけます。
その二点を通る 直線を引きます。
同じように 用紙の長方向を軸として 対象に直線を引きます。
90° 60° 30° の直角三角形が二つ クロスしている状態です。

三角形製作の作業方法は 前回の 五角形の作り方と同じとして 説明は省きます。
直角をはさむ二辺 265mm と 153mm とでできる角度は約 30.0003533° で
A4用紙に ミリメートルでの 整数比で表示できる 最も精度の高い角度です。
次は 291mm と 168mm とでできる角度で約 29.998682° です。
実際には 線を描く操作のなかで 様々なかたちで誤差の混入が生じます。
今まで説明のもとに 定寸法 定角度に 角材を整形できたとして話を進めます。
五角形で作る [3,5,3,5] は
二つの五角形の面が 58.2826° × 2 の角度で
かど が向かいあって接して結合されたユニットを
6 個 つくることを お勧めします。
上画像の 右下のユニットがそれです。
この六つのユニットの組み合わせで 簡単に 立体が完成します。
私は このユニット作成作業での接着は 木工用ボンドで行っています。
乾燥時の形状が
合成ゴム系ボンドでのものより しっかりしていると思っているからです。
粘性が弱く 完全接着まで時間がかかり 作業性に難があります。
その弱点克服に 私は 電子レンジを活用しています。
これは 私が 自己責任で 注意点をその都度確認しながら行っているものです。
お勧めしているものではありません。私の責任は回避します。
温め時間を 1 分とします。
コップ一杯の冷水を 温めます。飛散させないためその都度 冷水です。
コップは ガラス プラスチック 陶器などで
糊を含め 木材や 紙 を 一緒に温めることができます。
金属 は 不可です。金属製のうわぐすりのかかった陶器もです。
私の苦い経験では 木材だけを 1 分間暖めてしまい
台所が 霞に包まれたようになり きな臭さがなかなか消えませんでした。
面と面を接合させるための治具については 次回お話しします。
2015年10月2日
11[3,5,3,5] 多面体 製作道具
説明が 遅々として進んでいませんが [3,5,3,5] の話題をつづけます。
角棒で 正五角形をつくるための角度を表す シンプルな図を作ります。
角度をプロットするための用紙は 今まではグラフ用紙でしたが
今回は A4 のコピー用紙を用います。寸法は 210 × 297 ミリの 大きさです。
長い巾の方向に 紙のかどから 245mm のところに 印しをつけ。
短い巾の方向に 紙のかどから 178mm のところに 印しをつけます。
その二点を通る 直線を引きます。
下の画像の斜めの線がそれで 90° 54° 36° の直角三角形ができています。
用紙の 縦の直線と 斜線とでできた角度が 54° で
多角形を作る材料の 角棒と角棒が接するそれぞれの角度です。
画像右がわの 縦長の治具で 角棒を定寸でカットし 整形します。
これで作った部材が 60 個必要です。
正確な角度で 接合してゆくために
108° ( 54° + 54° ) に角度をつけた治具を作っておきます。
画像中ほどの 一番上がそれです。
この図では 54° は得られても 108° は無理です。
そこで この図に 現在 表示している斜線と左右対称になるよう
同じ方法で 用紙の左下かどから計測して斜線を引きます。

2015年9月30日
11[3,5,3,5] 多面体 諸量
前回 の続きとして [3,5,3,5] の 四角棒の多角形で作る方法をお伝えします。
5 角形 12 個 で作る方法と 3 角形 20 個 で作る方法の 2 つあると言いました。
まずは 5 角形で作る方法を お伝えします。
以下に 少し くどくどと 角度計算方法の説明から始めます。
最初に 正五角形の かどの角度 ( 内角 ) を求めてみます。
結果的には 180 – ( 360 / 5 ) = 108 として求まります。
正五角形の中心と 一つの辺とでできる二等辺三角形を考えます。
正五角形の一つの辺に対応する部分を 底辺 他の二つの辺を 等辺 とします。
底辺と等辺とでできる角度を 底角 等辺と等辺とでできる角度を頂角とします。
頂角は 360° を 角数の 5 で割ると求まり 72° です。
三角形の内角の和は 180° なので
頂角でない 他の二つの角度の合計は 180 – 72 の 108° です。
正五角形の かどの角度 ( 内角 ) は
隣り合う二つの 二等辺三角形の底角の和ですから
一つの二等辺三角形の底角の和と 同値です。つまり 108° です。
正五角形の一つの辺をつくる角棒の接合部分は
二等辺三角形の底角と同じで 108 / 2 の 54° です。
54° を直角を挟む 二辺の比として考えると
245/178 ( 54.0004° ) が近似値です。
正五角形の部品のみで作る 立体も 治具に正三角形を用いることもあるので
同じように計算した 角度を表示します。
三角形の接合角は 30° で 整数比は近似値 112/194 の 29.9987° です。
三角定規 ( 90° 60° 30° ) からも角度が得られます。
あと 製作に必要な数値は 五角形のかどから多面体の中芯までの かど・芯線と
五角形の面とでできる 面角です。
サイン x = 面芯寸 / 頂芯寸 で求められる x がその角度です。
つまり x = アークサイン ( 面芯寸 / 頂芯寸 ) で
arcsin ( 1.37638 / 1.61803 ) = 58.2826° となります。
58.2826° を直角を挟む 二辺の比として考えると
233/144 ( 58.2829° ) が近似値です。
エクセルでの 計算式を載せたかったのですが 弧度法表示が基本なため
度数表示に変換しなくてはならず煩雑になるため やめました。
関数電卓の使用をお勧めします。
文字ばかりの説明になってしまいました。ごめんなさい。
2015年9月18日
11[3,5,3,5] 多面体
多面体を今までとは違った方法で 作ってゆこうとして模索しています。
三角棒で レオナルドスタイル の 多面体を作る例をシリーズで お伝えしましたが
今回は 四角棒での 製作です。
下画像の 上の二つが このブログの初期から説明している方法で作ったもので
その左側の立体は 最近作った作品で ラミン材でできています。
下の二つが 今回説明しようとしている 製作方法で作っています。
どちらも ラミン材製です。

四角棒で多角形をつくり それで多面体に構築してゆくと
厚みのある多角形のため 面と面の接合部分には 溝ができてしまいます。
それを避けるために 接合部分を疑似的に線にする 三角棒を使っていました。
今回取り上げている [3,5,3,5] は 三角形 20個 または 5角形 12 個 のみで
多角形の かど だけの接合で 作ることができ 接合部分の加工が容易です。
上画像の下左が 五角形のみで 下右が 三角形のみでできています。
同じ素材で 三種類作っていますが 違いが判るでしょうか。
ラミン材はワシントン条約の 絶滅危惧種に属すため 手にできなかったのですが
最近 神戸三宮の 東急ハンズで 5×5mm の角材を買うことができました。
京都や大阪には どこの木材売り場にも 見つけられませんでした。
私にとっては レアものです。
しかし 丸棒のラミン材は ホームセンターでもよく見かけます。
木材業界のことは 私にはよくわかりません。
製作方法については 後日お伝えしようと思っています。
2015年8月18日
BASIC 多面体 諸量
すでにお伝えしている BASIC で記述した 諸量計算の 一般解を求めるプログラム の
出力データを載せておきます。( 2013年 1月 11日 掲載)
| | 名称 | 基本数 | | |
| ① | 仰角 | L接合角 | M接合角 | S接合角 |
| ② | 頂芯寸 | 稜芯寸 | | |
| ③ | L面芯寸 | M面芯寸 | S面芯寸 | |
| | | | |
| 01 | [3,3,3] | .577350269189627 | | |
| ① | 54.7356103172453 | 59.9999999999998 | 0 | 0 |
| ② | .612372435695795 | .353553390593275 | | |
| ③ | .204124145231932 | 0 | 0 | |
| | | | |
| 02 | [3,3,3,3] | .707106781186549 | | |
| ① | 44.9999999999999 | 44.9999999999999 | 0 | 0 |
| ② | .707106781186549 | .500000000000002 | | |
| ③ | .408248290463865 | 0 | 0 | |
| | | | |
| 03 | [4,4,4] | .816496580927728 | | |
| ① | 35.2643896827545 | 59.9999999999998 | 0 | 0 |
| ② | .866025403784443 | .707106781186553 | | |
| ③ | .500000000000007 | 0 | 0 | |
| | | | |
| 04 | [3,3,3,3,3] | .850650808352041 | | |
| ① | 31.7174744114609 | 35.9999999999999 | 0 | 0 |
| ② | .951056516295157 | .809016994374951 | | |
| ③ | .755761314076175 | 0 | 0 | |
| | | | |
| 05 | [3,4,3,4] | .86602540378444 | | |
| ① | 29.9999999999998 | 54.7356103172453 | 35.2643896827546 | 0 |
| ② | 1 | .866025403784444 | | |
| ③ | .707106781186547 | .816496580927726 | 0 | |
| | | | |
| 06 | [3,6,6] | .904534033733292 | | |
| ① | 25.2394018206788 | 73.2213451190395 | 33.5573097619207 | 0 |
| ② | 1.17260393995586 | 1.06066017177983 | | |
| ③ | .6123724356958 | 1.02062072615966 | 0 | |
| | | | |
| 07 | [3,3,3,3,4] | .928191377985573 | | |
| ① | 21.8453835538377 | 49.6241489558037 | 32.593962761049 | 0 |
| ② | 1.34371337374461 | 1.24722316799366 | | |
| ③ | 1.14261350892597 | 1.2133558000219 | 0 | |
| | | | |
| 08 | [3,4,4,4] | .933948831094466 | | |
| ① | 20.9410204722436 | 49.2105290590747 | 32.3684128227758 | 0 |
| ② | 1.39896632596592 | 1.30656296487639 | | |
| ③ | 1.20710678118656 | 1.27427369424832 | 0 | |
| | | | |
| 09 | [5,5,5] | .934172358962716 | | |
| ① | 20.9051574478893 | 59.9999999999999 | 0 | 0 |
| ② | 1.40125853844408 | 1.30901699437495 | | |
| ③ | 1.11351636441161 | 0 | 0 | |
| | | | |
| 10 | [4,6,6] | .948683298050515 | | |
| ① | 18.4349488229218 | 65.9051574478892 | 48.1896851042214 | 0 |
| ② | 1.58113883008421 | 1.50000000000002 | | |
| ③ | 1.22474487139162 | 1.41421356237312 | 0 | |
| | | | |
| 11 | [3,5,3,5] | .951056516295154 | | |
| ① | 17.9999999999999 | 58.2825255885389 | 31.717474411461 | 0 |
| ② | 1.6180339887499 | 1.53884176858763 | | |
| ③ | 1.37638192047118 | 1.51152262815235 | 0 | |
| | | | |
| 12 | [3,8,8] | .959682982260668 | | |
| ① | 16.3249499368951 | 74.3001425950404 | 31.399714809919 | 0 |
| ② | 1.77882364566394 | 1.70710678118656 | | |
| ③ | 1.20710678118657 | 1.68252198471218 | 0 | |
| | | | |
| 13 | [3,3,3,3,5] | .972732850565597 | | |
| ① | 13.4106337207749 | 56.2732455172424 | 30.9316886206893 | 0 |
| ② | 2.15583737511568 | 2.09705383525213 | | |
| ③ | 1.98091594728188 | 2.07708965974325 | 0 | |
| | | | |
| 14 | [3,4,5,4] | .974607762378171 | | |
| ① | 12.9393184371117 | 56.1084942262822 | 46.5129222544782 | 30.8656612647612 |
| ② | 2.23295050941571 | 2.17625089948285 | | |
| ③ | 2.06457288070678 | 2.11803398874992 | 2.15701985252026 | |
| | | | |
| 15 | [4,6,8] | .976450976246514 | | |
| ① | 12.4589101916906 | 71.1133299584335 | 62.4876519255486 | 46.3990181160177 |
| ② | 2.3176109128928 | 2.26303343845375 | | |
| ③ | 1.91421356237313 | 2.09077027517606 | 2.20710678118658 | |
| | | | |
| 16 | [5,6,6] | .979432085486415 | | |
| ① | 11.6407231367704 | 62.154680232797 | 55.6906395344059 | 0 |
| ② | 2.47801865906766 | 2.42705098312489 | | |
| ③ | 2.26728394222856 | 2.32743843676637 | 0 | |
| | | | |
| 17 | [3,10,10] | .985721919281303 | | |
| ① | 9.69372389531445 | 74.759837717322 | 30.4803245653556 | 0 |
| ② | 2.96944901586351 | 2.92705098312496 | | |
| ③ | 2.48989828488292 | 2.91278116659653 | 0 | |
| | | | |
| 18 | [4,6,10] | .99131668954106 | | |
| ① | 7.55605404616849 | 73.614860764356 | 60.8810401895552 | 45.5040990460887 |
| ② | 3.80239449985143 | 3.76937712792185 | | |
| ③ | 3.44095480117809 | 3.66854248067273 | 3.73606797749993 | |
2015年8月4日
多面体 諸量
多面体を今までとは違った方法で 作ってゆこうとして模索しています。
その製作に必要な 諸量は 手元にある資料からではなく
このブログから得ることにしています。
自分で作成しているのに まとまりがなく 探すのに苦労することが多々あります。
そこで 6桁に桁数を 落として リストとしてまとめてみました。
多面体諸量 稜寸は1として
| | | 面積 | 体積 | 基本数 | 頂芯寸 | 稜芯寸 | S面芯寸 | M面芯寸 | L面芯寸 |
| 01 | [3,3,3] | 1.73205 | .117851 | .577350 | .612372 | .353553 | .204124 | | |
| 02 | [3,3,3,3] | 3.46410 | .471405 | .707107 | .707107 | .500000 | .408248 | | |
| 03 | [4,4,4] | 6.00000 | 1.00000 | .816497 | .866025 | .707107 | .500000 | | |
| 04 | [3,3,3,3,3 | 8.66025 | 2.18169 | .850651 | .951057 | .809017 | .755761 | | |
| 05 | [3,4,3,4] | 9.46410 | 2.35702 | .866025 | 1.00000 | .866025 | .816497 | .707107 | |
| 06 | [3,6,6] | 12.1244 | 2.71058 | .904534 | 1.17260 | 1.06066 | 1.02062 | .612372 | |
| 07 | [3,3,3,3,4 | 19.8564 | 7.88948 | .928191 | 1.34371 | 1.24722 | 1.21336 | 1.14261 | |
| 08 | [3,4,4,4] | 21.4641 | 8.71405 | .933949 | 1.39897 | 1.30656 | 1.27427 | 1.20711 | |
| 09 | [5,5,5] | 20.6457 | 7.66312 | .934172 | 1.40126 | 1.30902 | 1.11352 | | |
| 10 | [4,6,6] | 26.7846 | 11.3137 | .948683 | 1.58114 | 1.50000 | 1.41421 | 1.22474 | |
| 11 | [3,5,3,5] | 29.3060 | 13.8355 | .951057 | 1.61803 | 1.53884 | 1.51152 | 1.37638 | |
| 12 | [3,8,8] | 32.4347 | 13.5997 | .959683 | 1.77882 | 1.70711 | 1.68252 | 1.20711 | |
| 13 | [3,3,3,3,5 | 55.2867 | 37.6166 | .972733 | 2.15584 | 2.09705 | 2.07709 | 1.98092 | |
| 14 | [3,4,5,4] | 59.3060 | 41.6153 | .974608 | 2.23295 | 2.17625 | 2.15702 | 2.11803 | 2.06457 |
| 15 | [4,6,8] | 61.7552 | 41.7990 | .976451 | 2.31761 | 2.26303 | 2.20711 | 2.09077 | 1.91421 |
| 16 | [5,6,6] | 72.6073 | 55.2877 | .979432 | 2.47802 | 2.42705 | 2.32744 | 2.26728 | |
| 17 | [3,10,10] | 100.991 | 85.0397 | .985722 | 2.96945 | 2.92705 | 2.91278 | 2.48990 | |
| 18 | [4,6,10] | 174.292 | 206.803 | .991317 | 3.80239 | 3.76938 | 3.73607 | 3.66854 | 3.44095 |
| | 仰角 | S接合角 | M接合角 | L接合角 | S面角 | M面角 | L面角 | | 二面角1 | | 二面角2 |
| 01 | 54.7356 | 60.0000 | | | 35.2644 | | | SS | 70.5288 | | |
| 02 | 45.0000 | 45.0000 | | | 54.7356 | | | SS | 109.471 | | |
| 03 | 35.2644 | 60.0000 | | | 45.0000 | | | SS | 90.0000 | | |
| 04 | 31.7175 | 36.0000 | | | 69.0948 | | | SS | 138.190 | | |
| 05 | 30.0000 | 35.2644 | 54.7356 | | 70.5288 | 54.7356 | | SM | 125.264 | | |
| 06 | 25.2394 | 33.5573 | 73.2213 | | 74.2068 | 35.2644 | | SM | 109.471 | MM | 70.5288 |
| 07 | 21.8454 | 32.5940 | 49.6241 | | 76.6173 | 66.3661 | | SS | 153.235 | SM | 142.983 |
| 08 | 20.9410 | 32.3684 | 49.2105 | | 77.2356 | 67.5000 | | SM | 144.736 | MM | 135.000 |
| 09 | 20.9052 | 60.0000 | | | 58.2825 | | | SS | 116.565 | | |
| 10 | 18.4349 | 48.1897 | 65.9052 | | 70.5288 | 54.7356 | | SM | 125.264 | MM | 109.471 |
| 11 | 18.0000 | 31.7175 | 58.2825 | | 79.1877 | 63.4349 | | SM | 142.623 | | |
| 12 | 16.3249 | 31.3997 | 74.3001 | | 80.2644 | 45.0000 | | SM | 125.264 | MM | 90.0000 |
| 13 | 13.4106 | 30.9317 | 56.2732 | | 82.0877 | 70.8422 | | SS | 164.175 | SM | 152.930 |
| 14 | 12.9393 | 30.8657 | 46.5129 | 56.1085 | 82.3774 | 76.7175 | 71.5651 | SM | 159.095 | ML | 148.283 |
| 15 | 12.4589 | 46.3990 | 62.4877 | 71.1133 | 77.2356 | 67.5000 | 57.7644 | SM | 144.736 | SL | 135.000 |
| 16 | 11.6407 | 55.6906 | 62.1547 | | 73.5278 | 69.0948 | | SM | 142.623 | MM | 138.190 |
| 17 | 9.69372 | 30.4803 | 74.7598 | | 84.3401 | 58.2825 | | SM | 142.623 | MM | 116.565 |
| 18 | 7.55605 | 45.5041 | 60.8810 | 73.6149 | 82.3774 | 76.7175 | 65.9052 | SM | 159.095 | SL | 148.283 |
| | | | | | | | | | | |
| | | | | | | | | | | 二面角3 |
| 15 | | | | | | | | | | ML | 125.264 |
| 18 | | | | | | | | | | ML | 142.623 |
-----------------------------------------------
双対多面体諸量 稜芯寸はもとの多面体の稜芯寸とイコールとして
| | | 双対面積 | 双対体積 | 稜芯寸 | 面芯寸 | S頂芯寸 | M頂芯寸 | L頂芯寸 |
| 01 | [3,3,3] | 1.73205 | .117851 | .353553 | .204124 | .612372 | | |
| 02 | [3,3,3,3] | 3.00000 | .353553 | .500000 | .353553 | .612372 | | |
| 03 | [4,4,4] | 6.92820 | 1.33333 | .707107 | .577350 | 1.00000 | | |
| 04 | [3,3,3,3,3] | 7.88597 | 1.80902 | .809017 | .688191 | .866025 | | |
| 05 | [3,4,3,4] | 9.54594 | 2.38649 | .866025 | .750000 | .918559 | 1.06066 | |
| 06 | [3,6,6] | 17.9098 | 5.72756 | 1.06066 | .959403 | 1.10227 | 1.83712 | |
| 07 | [3,3,3,3,4] | 19.2994 | 7.44740 | 1.24722 | 1.15766 | 1.28204 | 1.36141 | |
| 08 | [3,4,4,4] | 21.5135 | 8.75069 | 1.30656 | 1.22026 | 1.33967 | 1.41421 | |
| 09 | [5,5,5] | 22.6728 | 9.24181 | 1.30902 | 1.22285 | 1.53884 | | |
| 10 | [4,6,6] | 30.1869 | 14.3189 | 1.50000 | 1.42302 | 1.59099 | 1.83712 | |
| 11 | [3,5,3,5] | 30.3381 | 14.8002 | 1.53884 | 1.46353 | 1.56665 | 1.72048 | |
| 12 | [3,8,8] | 42.6918 | 23.3137 | 1.70711 | 1.63828 | 1.73205 | 2.41421 | |
| 13 | [3,3,3,3,5] | 55.2805 | 37.5884 | 2.09705 | 2.03987 | 2.11721 | 2.22000 | |
| 14 | [3,4,5,4] | 59.7674 | 42.2554 | 2.17625 | 2.12099 | 2.19565 | 2.23607 | 2.29397 |
| 15 | [4,6,8] | 67.4248 | 49.6638 | 2.26303 | 2.20974 | 2.32038 | 2.44949 | 2.67542 |
| 16 | [5,6,6] | 75.5655 | 59.8764 | 2.42705 | 2.37713 | 2.53093 | 2.59808 | |
| 17 | [3,10,10] | 115.570 | 111.149 | 2.92705 | 2.88526 | 2.94139 | 3.44095 | |
| 18 | [4,6,10] | 183.196 | 228.179 | 3.76938 | 3.73665 | 3.80298 | 3.87298 | 4.12915 |
| S稜寸 | M稜寸 | L稜寸 | | 双対稜寸 S | | 双対稜寸 M | | 双対稜寸 L |
| 01 | .500000 | | | SS | 1.00000 | | | | |
| 02 | .353553 | | | SS | .707107 | | | | |
| 03 | .707107 | | | SS | 1.41421 | | | | |
| 04 | .309017 | | | SS | .618034 | | | | |
| 05 | .306186 | .612372 | | SM | .918559 | | | | |
| 06 | .300000 | 1.50000 | | SM | 1.80000 | MM | 3.00000 | | |
| 07 | .296733 | .545776 | | SS | .593465 | SM | .842509 | | |
| 08 | .295990 | .541196 | | SM | .837186 | MM | 1.08239 | | |
| 09 | .809017 | | | SS | 1.61803 | | | | |
| 10 | .530330 | 1.06066 | | SM | 1.59099 | MM | 2.12132 | | |
| 11 | .293893 | .769421 | | SM | 1.06331 | | | | |
| 12 | .292893 | 1.70711 | | SM | 2.00000 | MM | 3.41421 | | |
| 13 | .291450 | .728538 | | SS | .582900 | SM | 1.01999 | | |
| 14 | .291249 | .513743 | .725417 | SM | .804992 | ML | 1.23916 | | |
| 15 | .512670 | .937379 | 1.42707 | SM | 1.45005 | SL | 1.93974 | ML | 2.36445 |
| 16 | .717645 | .927051 | | SM | 1.64470 | MM | 1.85410 | | |
| 17 | .290089 | 1.80902 | | SM | 2.09911 | MM | 3.61803 | | |
| 18 | .504458 | .889829 | 1.68572 | SM | 1.39429 | SL | 2.19017 | ML | 2.57555 |
| | 二面角 | S仰角 | M仰角 | L仰角 | Sかど角/2 | Mかど角/2 | Lかど角/2 | SML接合角 |
| 01 | 70.5288 | 54.7356 | | | 30.0000 | | | 60 |
| 02 | 90.0000 | 35.2644 | | | 45.0000 | | | 60 |
| 03 | 109.471 | 45.0000 | | | 30.0000 | | | 45 |
| 04 | 116.565 | 20.9052 | | | 54.0000 | | | 60 |
| 05 | 120.000 | 19.4712 | 35.2644 | | 54.7356 | 35.2644 | | 60 45 |
| 06 | 129.521 | 15.7932 | 54.7356 | | 56.4427 | 16.7787 | | 60 30 |
| 07 | 136.309 | 13.3827 | 23.6339 | | 57.4060 | 40.3759 | | 60 45 |
| 08 | 138.118 | 12.7644 | 22.5000 | | 57.6316 | 40.7895 | | 60 45 |
| 09 | 138.190 | 31.7175 | | | 30.0000 | | | 36 |
| 10 | 143.130 | 19.4712 | 35.2644 | | 41.8103 | 24.0948 | | 45 30 |
| 11 | 144.000 | 10.8123 | 26.5651 | | 58.2825 | 31.7175 | | 60 36 |
| 12 | 147.350 | 9.73561 | 45.0000 | | 58.6003 | 15.6999 | | 60 22.5 |
| 13 | 153.179 | 7.91232 | 19.1578 | | 59.0683 | 33.7268 | | 60 36 |
| 14 | 154.121 | 7.62263 | 13.2825 | 18.4349 | 59.1343 | 43.4871 | 33.8915 | 60 45 36 |
| 15 | 155.082 | 12.7644 | 22.5000 | 32.2356 | 43.6010 | 27.5123 | 18.8867 | 45 30 22.5 |
| 16 | 156.719 | 16.4722 | 20.9052 | | 34.3094 | 27.8453 | | 36 30 |
| 17 | 160.613 | 5.65989 | 31.7175 | | 59.5197 | 15.2402 | | 60 18 |
| 18 | 164.888 | 7.62263 | 13.2825 | 24.0948 | 44.4959 | 29.1190 | 16.3851 | 45 30 18 |
2015年7月26日
11[3,5,3,5] 多面体 製作道具
[3,5,3,5] の レオナルドスタイル双対多面 を作成している途中の画像です。
パーツを接着して 菱形のユニットを 30 個そろえる作業は完了しました。
菱形のユニットは 木工用ボンドで接合しています。
それらを 今度は 合成ゴム系ボンドで くっつけてゆきます。
下の画像の説明をします。
右 中ほどの 四角形の治具だけで 今回のパーツはできています。
四角形の断面の角棒を 必要な角度と寸法にカットし成形するための治具です。
溝の面は 45 度 と 45 度 で向き合っています。
この治具に 少しは判りやすいかと 3倍の寸法の角材を乗せています。
この角材は 底面と底面を水平に合わせた 三角棒を セロテープで縛っています。
この治具で加工し テープをとって広げると その左上のような
傾斜型 ( 前々回お伝えしています ) の形状にできます。
今回の 求める形状は 菱形なので 稜寸は 1 種類で 接合角も実質 1 種類です。
かどが 90 度の形状の板に 58.283 度 ( 233 / 144 ) の角度の溝を
かどを挟んで付けると もう一方の側の溝の角度は 90 – 58.283 で
31.717 度 ( 144 / 233 ) になり 必要な角度が得られます。
治具の中の 山がたにしたものは
鋭角方向で接着した 菱形の 1/2 の形状部品を整形するものです。
角度のチェックと 鈍角側の接合角と 稜寸を整えます。

上に説明した方法で 菱形が正確にできれば 後の接合は簡単です。
菱形の鈍角は 三つを 1 点に合わせ
鋭角は 1 点に 五つを合わせるというルールだけです。

上画像の多面体を乗せているのは 最近つくった 作業台です。
とても重宝しています。
ざらつきの 表面加工がされている
250mm × 350mm 4mm 厚 の強化ガラスのキッチンプレートと
5mm × 15mm の棒材で 3mm ほどの高さに縁どりした
300mm × 450mm のファルカタ集成材です。
プレートの裏には キッチングッズを絵にした フィルムが張られていました。
それを剥がすのにすこし苦労しましたが 頑張りました。 いい出来です。
¥100 で get したことでも気に入っています。
四隅に防振クッションをつけています。
2015年7月22日
11[3,5,3,5] Excel 多面体 諸量
多面体の製作方法を [3,5,3,5] を例にして シリーズでお伝えしています。
つぎは [3,5,3,5] の双対多面体の 三角棒での作り方を 考えているのですが
面と面でつくるための 接合角の数値算出の資料がありませんでした。
そこで 双対多面体の 面積と 体積 も含めた
Excel での計算式が出来ましたので 載せておきます。
この計算式は 菱形の面をつくる 接合角の値を出したくて作りました。
下が その出力の一部です。
元の多面体の稜寸を 1 としたときの
0.293892626146237 + 0.769420884293813 = 1.06331351044005
が 正三角形と正五角形をまたぐ稜の寸法で これ一種類です。
三角形の上にくる双対の稜は 58.2825255885389 度ずつで左右結合され
五角形の上にくる双対の稜は 31.717474411461 度ずつで左右結合される
菱形の面をもつ 多面体になります。
そのときの 面積は 30.3381372890605 になり
体積は 14.8002124296868 になります。
| 角数 | 個数 | 双稜寸 | 稜開き角/2 | 双対面積 |
| 3 | 20 | 0.293892626146237 | 58.2825255885389 | 30.3381372890605 |
| 5 | 12 | 0.769420884293813 | 31.717474411461 | 双対体積 |
| 0 | 0 | 0 | 0 | 14.8002124296868 |

上は 四角棒で作った 以前にもお伝えしている作品です。右が双対多面体です。
三角棒では まだできていません。
詳しくは 次回にお伝えしようと思っています。
Excel の計算式です。
色付けした全範囲を指定し 1 行目 A 列に copy and paste
隠れた部分もありますが 全範囲を指定すれば コピーできます。
| | 名称 | S角数 | M角数 | L角数 | S面数 | M面数 | L面数 | 頂芯寸 |
| 11 | [3,5,3,5] | 3 | 5 | 0 | 20 | 12 | 0 | 1.61803398874989 |
| | | | | | | | |
| 角数 | 個数 | 多角形のかど心寸 | 面芯寸 | 多角形の辺心寸 | 面積 | 体積 | | |
| =C2 | =F2 | =0.5/SIN(PI()/A5) | =SQRT($I$2^2-C5^2) | =0.5/TAN(PI()/A5) | =E5/2*A5*B5 | =F5*D5/3 | 総面積 | =SUM(F5:F7) |
| =D2 | =G2 | =IF(B6>0,0.5/SIN(PI()/A6),0) | =IF(B6>0,SQRT($I$2^2-C6^2),0) | =IF(B6>0,0.5/TAN(PI()/A6),0) | =IF(B6>0,E6/2*A6*B6,0) | =IF(B6>0,F6*D6/3,0) | | |
| =E2 | =H2 | =IF(B7>0,0.5/SIN(PI()/A7),0) | =IF(B7>0,SQRT($I$2^2-C7^2),0) | =IF(B7>0,0.5/TAN(PI()/A7),0) | =IF(B7>0,E7/2*A7*B7,0) | =IF(B7>0,F7*D7/3,0) | 総体積 | =SUM(G5:G7) |
| | | | | | | | |
| | かど角/2 | かど心寸 | 辺心寸 | 稜芯寸 | 心・かど・芯角 | 双頂芯寸 | 双面芯寸 |
| =A5 | =B5 | =PI()/2-PI()/A10 | =0.5/COS(C10) | =0.5*TAN(C10) | =SQRT(I2^2-0.5^2) | =ACOS(D10/I2) | =F10^2/D5 | =H10*SIN(G10) |
| =A6 | =B6 | =IF(B11>0,PI()/2-PI()/A11,0) | =IF(B11>0,0.5/COS(C11),0) | =IF(B11>0,0.5*TAN(C11),0) | =IF(B11>0,F10,"") | =IF(B11>0,ACOS(D11/I2),"") | =IF(B11>0,F11^2/D6,"") | =IF(B11>0,H11*SIN(G11),"") |
| =A7 | =H2 | =IF(B12>0,PI()/2-PI()/A12,0) | =IF(B12>0,0.5/COS(C12),0) | =IF(B12>0,0.5*TAN(C12),0) | =IF(B12>0,F11,0) | =IF(B12>0,ACOS(D12/I2),0) | =IF(B12>0,F12^2/D7,0) | =IF(B12>0,H12*SIN(G12),0) |
| | | | | | | | |
| | 双菱形長寸 | 双菱形短寸/2 | 個別双面積 | 個別双体積 | 双稜寸 | 稜開き角/2 | 双対面積 |
| =A10 | =B10 | =H10*COS(G10) | =0.5*SIN(C10) | =C15*D15*A15*B15 | =E15*I10/3 | =SQRT(H10^2-F10^2) | =DEGREES(ASIN(D15/G15)) | =SUM(E15:E17) |
| =A11 | =B11 | =IF(B16>0,H11*COS(G11),0) | =IF(B16>0,0.5*SIN(C11),0) | =IF(B16>0,C16*D16*A16*B16,0) | =IF(B16>0,E16*I11/3,0) | =IF(B16>0,SQRT(H11^2-F11^2),0) | =IF(B16>0,DEGREES(ASIN(D16/G16)),0) | 双対体積 |
| =A12 | =B12 | =IF(B17>0,H12*COS(G12),0) | =IF(B17>0,0.5*SIN(C12),0) | =IF(B17>0,C17*D17*A17*B17,0) | =IF(B17>0,E17*I12/3,0) | =IF(B17>0,SQRT(H12^2-F12^2),0) | =IF(B17>0,DEGREES(ASIN(D17/G17)),0) | =SUM(F15:F17) |
| |
色付けした全範囲を指定し 19 行目 A 列に copy and paste
これは データ資料であり
必要な数値を求めるときに 2 行目 A 列に 各行を copy and paste してください。
| | 名称 | S角数 | M角数 | L角数 | S面数 | M面数 | L面数 | 頂芯寸 |
| 01 | [3,3,3] | 3 | 0 | 0 | 4 | 0 | 0 | 0.612372435695794 |
| 02 | [3,3,3,3] | 3 | 0 | 0 | 8 | 0 | 0 | 0.707106781186547 |
| 03 | [4,4,4] | 4 | 0 | 0 | 6 | 0 | 0 | 0.866025403784438 |
| 04 | [3,3,3,3,3] | 3 | 0 | 0 | 20 | 0 | 0 | 0.951056516295153 |
| 05 | [3,4,3,4] | 3 | 4 | 0 | 8 | 6 | 0 | 1 |
| 06 | [3,6,6] | 3 | 6 | 0 | 4 | 4 | 0 | 1.17260393995585 |
| 07 | [3,3,3,3,4] | 3 | 4 | 0 | 32 | 6 | 0 | 1.3437133737446 |
| 08 | [3,4,4,4] | 3 | 4 | 0 | 8 | 18 | 0 | 1.3989663259659 |
| 09 | [5,5,5] | 5 | 0 | 0 | 12 | 0 | 0 | 1.40125853844407 |
| 10 | [4,6,6] | 4 | 6 | 0 | 6 | 8 | 0 | 1.58113883008418 |
| 11 | [3,5,3,5] | 3 | 5 | 0 | 20 | 12 | 0 | 1.61803398874989 |
| 12 | [3,8,8] | 3 | 8 | 0 | 8 | 6 | 0 | 1.77882364566392 |
| 13 | [3,3,3,3,5] | 3 | 5 | 0 | 80 | 12 | 0 | 2.15583737511563 |
| 14 | [3,4,5,4] | 3 | 4 | 5 | 20 | 30 | 12 | 2.23295050941569 |
| 15 | [4,6,8] | 4 | 6 | 8 | 12 | 8 | 6 | 2.31761091289276 |
| 16 | [5,6,6] | 5 | 6 | 0 | 12 | 20 | 0 | 2.47801865906761 |
| 17 | [3,10,10] | 3 | 10 | 0 | 20 | 12 | 0 | 2.96944901586339 |
| 18 | [4,6,10] | 4 | 6 | 10 | 30 | 20 | 12 | 3.80239449985129 |
| |
2015年7月19日
11[3,5,3,5] 多面体
[3,5,3,5] の製作説明をしようと思います。
レオナルド ダ ヴィンチの 挿絵にある多面体 Leonardo da Vinci’s Polyhedra
( 多面体研究家 George W. Hart さんの webpage にリンク )
に形状を似せたものを 今回はお伝えします。
いつも使用している角材と違って 三角棒を用います。
断面は 正四角形を対角線で 二つに分けた形状 (直角二等辺三角形)です。
なぜ三角棒を用いるか説明します。
今まで お伝えしていた多面体製作の方法は 多面体の面ではなく
面と面でできる線つまり 稜線を 何かの材料でどう正確に表現するか でした。
今回のは 何かの材料で 正確な多角形を表す平面を複数つくり
それらの辺を接合し立体を作る というものです。
多角形を作る材を 四角の断面をもつ角棒にすると
それぞれの多角形の接合部分には V字型の溝ができてしまいます。
正多角形の辺を作る角材の 側面と多角形の平面とでできる角度は 90° です。
つまり 90°の面角を持った 厚みのある多角形どうしの結合では
二面角が 180°になってしまい 立体の製作は不可能です。
三角棒の面角は 90° と 45° と 45° です。
三角棒を 多角形を縁取る frame とする場合 内側の材の面角は
90° (絶壁型)と 45°(傾斜型) の二種類が考えられますが
傾斜型 のほうが 絶壁型 より 加工は楽です。
でも 傾斜型は下手をすると 小さな穴のあいた多角形を作ってしまいます。
出来るだけ 細めの材を使うといいでしょう。
このブログで お伝えしている 18種類の多面体の 二面角は
[3,3,3] と [3,6,6] を除いてすべて 90°以上なので この方法で製作可能です。
下の画像は [3,5,3,5] で 6mm の角材を 斜めカットされた 角棒で作っています。
長さは 23mm 絶壁型 です。
三角形の接合角は 30° ( 112/194 ) 五角形は 54° ( 245/178 ) です。
接着剤は 合成ゴム系を用います。
接着部分の可塑性がしばらく残るので
厚紙を切り抜いて多面体を作るのと同じような 感覚です。
左側の形状が 右のような組み合わせで作ったもので 二つ合わせて完成です。

[3,3,3] とその複合多面体

[3,6,6] とその双対多面体
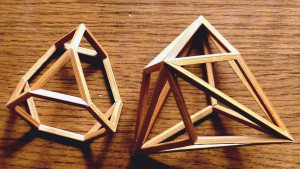
2015年7月8日
多面体 未分類
今 [3,5,3,5] の製作方法について あれやこれやと考えているのですが。
作り方のこと その画像 そして文字での表現 等々 大変です。
参考にしたり 例示したりする資料が 木工では少ないのです。
その点 折り紙での製作は 奥深いものがあります。
以下の 画像は 手元にある 折り紙多面体 関連書籍です。
川村みゆきさん 布施知子さん 堀井洋子さん となぜか女性ばかりです。

折り紙は工芸としても 魅力がありますが
それの数学的理解や解釈に興味深いものがあります。
TEDというプレゼンテーションの動画サイトがあります。
日本語版もあります。
ロバート・ラングが全く新しい時代の折り紙を折るという動画を紹介します。
デジタルキャスト版もあります。

折り紙はアート であり 彫刻だ として
数学の原理を 芸術に当てはめ 背景にある法則が発見されていると言っています。
このプレゼンテーションを
NHKも「折り紙の数学と魔法」という題で放映していました。
NHK 7月22日(水)の番組予定はイ・ジンハとジョセフ・デシモーン
「驚異の超高速3Dプリンター」だそうです。 *注
What if 3D printer was 100x faster?
Reach into the computer and grab a pixel
3Dプリンターは 今後 ますます多面体つくりの有力なツールの一つになると思います。
* NHKはBBCなどと比べて アーカイブの扱いに対し 相当ズサンだと感じています。
2015年6月30日
Excel 多面体 諸量
前回
一つの頂でてきる 多角錐から 諸量計算が簡単にできる多面体は多くあります。
と言いました。
以下に Excel での計算を 載せておきます。
[3,3,3,3,4] [3,3,3,3,5] [4,6,8] [4,6,10] は 保留します。
[3,4,5,4] は 式が複雑になってしまって 簡単ではありませんでした。
それらは パズル気分で 処理する Excel や
一般解を求める BASIC で処理したほうが得策のようです。
色付けした全範囲を指定し 1 行目 A 列に copy and paste
| | 角数 | 側角度(R) | かど開き寸/2 | かど開き寸 |
| | 3 | =PI()/B2 | =COS(C2) | =D2*2 |
| | 4 | =PI()/B3 | =COS(C3) | =D3*2 |
| | 5 | =PI()/B4 | =COS(C4) | =D4*2 |
| | 6 | =PI()/B5 | =COS(C5) | =D5*2 |
| | 8 | =PI()/B6 | =COS(C6) | =D6*2 |
| | 10 | =PI()/B7 | =COS(C7) | =D7*2 |
| | | | | |
| | | かど・中心寸 | 頂・底心寸 | 外接球半径 |
| 1 | [3,3,3] | =(SQRT(3)/2)/3*2 | =SQRT(1-C10^2) | =0.5/D10 |
| 2 | [3,3,3,3] | =1/SQRT(2) | =SQRT(1-C11^2) | =0.5/D11 |
| 3 | [4,4,4] | =SQRT(2)*(SQRT(3)/2)/3*2 | =SQRT(1-C12^2) | =0.5/D12 |
| 4 | [3,3,3,3,3] | =0.5/SIN(PI()/5) | =SQRT(1-C13^2) | =0.5/D13 |
| 5 | [3,4,3,4] | =SQRT(1+E3^2)/2 | =SQRT(1-C14^2) | =0.5/D14 |
| 6 | [3,6,6] | =E5/SQRT(E5^2-D2^2)*D5 | =SQRT(1-C15^2) | =0.5/D15 |
| 7 | [3,3,3,3,4] | | | |
| 8 | [3,4,4,4] | =(0.5*E3)/COS(ACOS(((E3-1)/2)/E3)/2) | =SQRT(1-C17^2) | =0.5/D17 |
| 9 | [5,5,5] | =E4*SQRT(3)/2/3*2 | =SQRT(1-C18^2) | =0.5/D18 |
| 10 | [4,6,6] | =E5/SQRT(E5^2-D3^2)*D5 | =SQRT(1-C19^2) | =0.5/D19 |
| 11 | [3,5,3,5] | =SQRT(1+E4^2)/2 | =SQRT(1-C20^2) | =0.5/D20 |
| 12 | [3,8,8] | =E6/SQRT(E6^2-D2^2)*D6 | =SQRT(1-C21^2) | =0.5/D21 |
| 13 | [3,3,3,3,5] | | | |
| 14 | [3,4,5,4] | | | |
| 15 | [4,6,8] | | | |
| 16 | [5,6,6] | =E5/SQRT(E5^2-D4^2)*D5 | =SQRT(1-C25^2) | =0.5/D25 |
| 17 | [3,10,10] | =E7/SQRT(E7^2-D2^2)*D7 | =SQRT(1-C26^2) | =0.5/D26 |
| 18 | [4,6,10] | | | |
以下のような 表示になります。
| | 角数 | 側角度(R) | かど開き寸/2 | かど開き寸 |
| | 3 | 1.0471975511966 | 0.5 | 1 |
| | 4 | 0.785398163397448 | 0.707106781186548 | 1.4142135623731 |
| | 5 | 0.628318530717959 | 0.809016994374947 | 1.61803398874989 |
| | 6 | 0.523598775598299 | 0.866025403784439 | 1.73205080756888 |
| | 8 | 0.392699081698724 | 0.923879532511287 | 1.84775906502257 |
| | 10 | 0.314159265358979 | 0.951056516295154 | 1.90211303259031 |
| | | | | |
| | | かど・中心寸 | 頂・底心寸 | 外接球半径 |
| 1 | [3,3,3] | 0.577350269189626 | 0.816496580927726 | 0.612372435695794 |
| 2 | [3,3,3,3] | 0.707106781186547 | 0.707106781186548 | 0.707106781186547 |
| 3 | [4,4,4] | 0.816496580927726 | 0.577350269189626 | 0.866025403784439 |
| 4 | [3,3,3,3,3] | 0.85065080835204 | 0.525731112119134 | 0.951056516295153 |
| 5 | [3,4,3,4] | 0.866025403784439 | 0.5 | 1 |
| 6 | [3,6,6] | 0.904534033733291 | 0.426401432711221 | 1.17260393995586 |
| 7 | [3,3,3,3,4] | | | |
| 8 | [3,4,4,4] | 0.933948831094465 | 0.357406744336593 | 1.39896632596591 |
| 9 | [5,5,5] | 0.934172358962716 | 0.35682208977309 | 1.40125853844407 |
| 10 | [4,6,6] | 0.948683298050514 | 0.316227766016838 | 1.58113883008419 |
| 11 | [3,5,3,5] | 0.951056516295154 | 0.309016994374948 | 1.61803398874989 |
| 12 | [3,8,8] | 0.959682982260667 | 0.28108463771482 | 1.77882364566393 |
| 13 | [3,3,3,3,5] | | | |
| 14 | [3,4,5,4] | | | |
| 15 | [4,6,8] | | | |
| 16 | [5,6,6] | 0.979432085486414 | 0.201774106167599 | 2.47801865906762 |
| 17 | [3,10,10] | 0.985721919281302 | 0.168381405886715 | 2.96944901586339 |
| 18 | [4,6,10] | | | |
2015年6月17日
11[3,5,3,5] 多面体
2012年5月3日 にブログを立ち上げ 最初に載せた画像が [3,5,3,5] でした。
製作の 一番のお勧めとしてあげる多面体といえば これです。
下左の画像は ヒノキ 5 × 5 mm の角材で 数日前に作った作品です。
説明の例として あらためて作ったものです。ラフな仕上がりです。

エクセルでの 多面体の諸量計算を
一般的解法としてパズルのように解いてゆくのではなく
個別に 計算してゆく方法をお伝えします。
[3,5,3,5] は 正三角形と正五角形が 一つの頂に
3 5 3 5 と並んだ組み合わせのみでできています。
そして 全ての頂が 一つの球に接することができます。
このことから 稜の寸法も一つ 稜から中芯までの距離も一つで
稜と中芯とでできる三角形は 二等辺です。
正多角形の一つのかどで 隣り合う辺を斜辺とする二等辺三角形の
底辺の長さを かど開き寸とします。
計算に入ります。
画像右下の長方形を底とする 四角錐の高さを求めます。
稜の長さを 1 とします。
三角形の かど開き寸 は 1.
五角形の かど開き寸 は cos ( 360 ÷ 5 × 1 / 2 ) × 2 = 1.61803398874989
四角錐の底面長方形の対角線の長さは
1.61803398874989 の二乗と 1 を足した値の 平方根 ⇒ 1.90211303259031
四角錐の底面のかどから底面の中点までの長さは
1.90211303259031 ÷ 2 = 0.951056516295154
四角錐の高さは
稜の長さ の二乗 1 から 0.951056516295154 の二乗 0.904508497187474 を引いた値
0.0954915028125264 の 平方根 ⇒ 0.309016994374948
稜と中芯とでできる三角形は 二等辺だといいました。
つまり 稜と 角錐の高さとでできる角度は
頂から多面体の中芯までの距離と 稜の 1/2 の寸法でできる角度と同じです。
頂から多面体の中芯までの距離は
0.5 ÷ 0.309016994374948 = 1.61803398874989
上記の諸量の値は Excel で 計算しながら記述したものです。
1.6180339887498948482が より精度の高い値です。
頂から多面体の中芯までの距離は 外接球半径と呼ばれ
これが判ればあとは 芋づる式に数値が求められます。
( このブログでは 外接球半径を 同じ意味で 頂芯寸 という用語で説明しています。)
このように 一つの頂でてきる 多角錐から 諸量計算が簡単にできる多面体は多くあります。
[ 3,3,3,3,4 ] や [ 3,3,3,3,5 ] は無理でしょう
[ 4,6,8 ] や [ 4,6,10 ] などは むつかしいです。
2015年6月16日
sphericity 多面体 諸量
シリーズで 諸量の計算について お伝えしてきました。
その 計算結果の値や内容の信頼性を高めるために Wikipedia や
Wolfram Alpha そして MathWorld を参考にすることがあります。
ただ 検索に必要な 名称がつかみにくく 手間取ることが多くあります。
以下に 検索できる 名称と webpage をリンクさせた 一覧表を載せておきます。
日本語版のWikipedia
|
|
多面体 |
双対多面体 |
| 01 |
[3,3,3] |
正4面体 |
正4面体 |
| 02 |
[3,3,3,3] |
正8面体 |
正6面体 |
| 03 |
[4,4,4] |
正6面体 |
正8面体 |
| 04 |
[3,3,3,3,3] |
正20面体 |
正12面体 |
| 05 |
[3,4,3,4] |
立方8面体 |
菱形12面体 |
| 06 |
[3,6,6] |
切頂4面体 |
3方4面体 |
| 07 |
[3,3,3,3,4] |
変形立方体 |
5角24面体 |
| 08 |
[3,4,4,4] |
斜方立方8面体 |
凧形24面体 |
| 09 |
[5,5,5] |
正12面体 |
正20面体 |
| 10 |
[4,6,6] |
切頂8面体 |
4方6面体 |
| 11 |
[3,5,3,5] |
20・12面体 |
菱形30面体 |
| 12 |
[3,8,8] |
切頂6面体 |
3方8面体 |
| 13 |
[3,3,3,3,5] |
変形12面体 |
5角60面体 |
| 14 |
[3,4,5,4] |
斜方20・12面体 |
凧形60面体 |
| 15 |
[4,6,8] |
斜方切頂立方8面体 |
6方8面体 |
| 16 |
[5,6,6] |
切頂20面体 |
5方12面体 |
| 17 |
[3,10,10] |
切頂12面体 |
3方20面体 |
| 18 |
[4,6,10] |
斜方切頂20・12面体 |
6方20面体 |
英語版のWikipedia
|
|
polyhedron |
dual polyhedron |
| 01 |
[3,3,3] |
Tetrahedron |
Tetrahedron |
| 02 |
[3,3,3,3] |
Octahedron |
Cube |
| 03 |
[4,4,4] |
Cube |
Octahedron |
| 04 |
[3,3,3,3,3] |
Icosahedron |
Dodecahedron |
| 05 |
[3,4,3,4] |
Cuboctahedron |
Rhombic dodecahedron |
| 06 |
[3,6,6] |
Truncated tetrahedron |
Triakis tetrahedron |
| 07 |
[3,3,3,3,4] |
Snub cube |
Pentagonal icositetrahedron |
| 08 |
[3,4,4,4] |
Rhombicuboctahedron |
Deltoidal icositetrahedron |
| 09 |
[5,5,5] |
Dodecahedron |
Icosahedron |
| 10 |
[4,6,6] |
Truncated octahedron |
Tetrakis hexahedron |
| 11 |
[3,5,3,5] |
Icosidodecahedron |
Rhombic triacontahedron |
| 12 |
[3,8,8] |
Truncated cube |
Triakis octahedron |
| 13 |
[3,3,3,3,5] |
Snub dodecahedron |
Pentagonal hexecontahedron |
| 14 |
[3,4,5,4] |
Rhombicosidodecahedron |
Deltoidal hexecontahedron |
| 15 |
[4,6,8] |
Truncated cuboctahedron |
Disdyakis dodecahedron |
| 16 |
[5,6,6] |
Truncated icosahedron |
Pentakis dodecahedron |
| 17 |
[3,10,10] |
Truncated dodecahedron |
Triakis icosahedron |
| 18 |
[4,6,10] |
Truncated icosidodecahedron |
Disdyakis triacontahedron |
Wolfram Alpha
|
|
polyhedron |
dual polyhedron |
| 01 |
[3,3,3] |
tetrahedron |
tetrahedron |
| 02 |
[3,3,3,3] |
octahedron |
cube |
| 03 |
[4,4,4] |
cube |
octahedron |
| 04 |
[3,3,3,3,3] |
icosahedron |
dodecahedron |
| 05 |
[3,4,3,4] |
cuboctahedron |
rhombic dodecahedron |
| 06 |
[3,6,6] |
truncated tetrahedron |
triakis tetrahedron |
| 07 |
[3,3,3,3,4] |
snub cube |
pentagonal icositetrahedron |
| 08 |
[3,4,4,4] |
rhombicuboctahedron |
deltoidal icositetrahedron |
| 09 |
[5,5,5] |
dodecahedron |
icosahedron |
| 10 |
[4,6,6] |
truncated octahedron |
tetrakis hexahedron |
| 11 |
[3,5,3,5] |
icosidodecahedron |
rhombic triacontahedron |
| 12 |
[3,8,8] |
truncated cube |
small triakis octahedron |
| 13 |
[3,3,3,3,5] |
snub dodecahedron |
pentagonal hexecontahedron |
| 14 |
[3,4,5,4] |
rhombicosidodecahedron |
deltoidal hexecontahedron |
| 15 |
[4,6,8] |
truncated cuboctahedron |
disdyakis dodecahedron |
| 16 |
[5,6,6] |
truncated icosahedron |
pentakis dodecahedron |
| 17 |
[3,10,10] |
truncated dodecahedron |
triakis icosahedron |
| 18 |
[4,6,10] |
truncated icosidodecahedron |
disdyakis triacontahedron |
MathWorld
|
|
polyhedron |
dual polyhedron |
| 01 |
[3,3,3] |
Regular Tetrahedron |
Regular Tetrahedron |
| 02 |
[3,3,3,3] |
Octahedron |
Cube |
| 03 |
[4,4,4] |
Cube |
Octahedron |
| 04 |
[3,3,3,3,3] |
Icosahedron |
Dodecahedron |
| 05 |
[3,4,3,4] |
Cuboctahedron |
Rhombic Dodecahedron |
| 06 |
[3,6,6] |
Truncated Tetrahedron |
Triakis Tetrahedron |
| 07 |
[3,3,3,3,4] |
Snub Cube |
Pentagonal Icositetrahedron |
| 08 |
[3,4,4,4] |
Small Rhombicuboctahedron |
Deltoidal Icositetrahedron |
| 09 |
[5,5,5] |
Dodecahedron |
Icosahedron |
| 10 |
[4,6,6] |
Truncated Octahedron |
Tetrakis Hexahedron |
| 11 |
[3,5,3,5] |
Icosidodecahedron |
Rhombic Triacontahedron |
| 12 |
[3,8,8] |
Truncated Cube |
Small Triakis Octahedron |
| 13 |
[3,3,3,3,5] |
Snub Dodecahedron |
Pentagonal Hexecontahedron |
| 14 | [3,4,5,4] | Small Rhombicosidodecahedron | Deltoidal Hexecontahedron | |
15 |
[4,6,8] |
Great Rhombicuboctahedron |
Disdyakis Dodecahedron |
| 16 |
[5,6,6] |
Truncated Icosahedron |
Pentakis Dodecahedron |
| 17 |
[3,10,10] |
Truncated Dodecahedron |
Tiakis Icosahedron |
| 18 |
[4,6,10] |
Great Rhombicosidodecahedron |
Disdyakis Triacontahedron |
2015年6月12日
Excel 多面体 諸量
今回も 多面体諸量をExcel で求める方法をお伝えしています。
面積と 体積の 算出です。
色付けした全範囲を指定し 1 行目 A 列に copy and paste
| | 名称 | S角数 | M角数 | L角数 |
| 1 | [3,3,3] | 3 | 2 | 2 |
| | | | |
| 角数 | 個数 | 多角形のかど心寸 | 面芯寸 | 多角形の辺心寸 |
| =C2 | =F2 | =0.5/SIN(PI()/A5) | =SQRT($I$2^2-C5^2) | =0.5/TAN(PI()/A5) |
| =D2 | =G2 | =0.5/SIN(PI()/A6) | =SQRT($I$2^2-C6^2) | =0.5/TAN(PI()/A6) |
| =E2 | =H2 | =0.5/SIN(PI()/A7) | =SQRT($I$2^2-C7^2) | =0.5/TAN(PI()/A7) |
色付けした全範囲を指定し 1 行目 F 列に copy and paste
| S面数 | M面数 | L面数 | 頂芯寸 |
| 4 | 0 | 0 | 0.612372435695795 |
| | | |
| 面積 | 体積 | | |
| =E5/2*A5*B5 | =F5*D5/3 | 総面積 | =SUM(F5:F7) |
| =E6/2*A6*B6 | =F6*D6/3 | | |
| =E7/2*A7*B7 | =F7*D7/3 | 総体積 | =SUM(G5:G7) |
色付けした全範囲を指定し 9 行目 A 列に copy and paste
これは データ資料であり
必要な数値を求めるときに 2 行目 A 列に 各行を copy and paste してください。
| | 名称 | S角数 | M角数 | L角数 | S面数 | M面数 | L面数 | 頂芯寸 |
| 1 | [3,3,3] | 3 | 2 | 2 | 4 | 0 | 0 | 0.612372435695795 |
| 2 | [3,3,3,3] | 3 | 2 | 2 | 8 | 0 | 0 | 0.707106781186548 |
| 3 | [4,4,4] | 4 | 2 | 2 | 6 | 0 | 0 | 0.866025403784438 |
| 4 | [3,3,3,3,3] | 3 | 2 | 2 | 20 | 0 | 0 | 0.951056516295154 |
| 5 | [3,4,3,4] | 3 | 4 | 2 | 8 | 6 | 0 | 1 |
| 6 | [3,6,6] | 3 | 6 | 2 | 4 | 4 | 0 | 1.17260393995586 |
| 7 | [3,3,3,3,4] | 3 | 4 | 2 | 32 | 6 | 0 | 1.34371337374461 |
| 8 | [3,4,4,4] | 3 | 4 | 2 | 8 | 18 | 0 | 1.39896632596591 |
| 9 | [5,5,5] | 5 | 2 | 2 | 12 | 0 | 0 | 1.40125853844408 |
| 10 | [4,6,6] | 4 | 6 | 2 | 6 | 8 | 0 | 1.58113883008419 |
| 11 | [3,5,3,5] | 3 | 5 | 2 | 20 | 12 | 0 | 1.6180339887499 |
| 12 | [3,8,8] | 3 | 8 | 2 | 8 | 6 | 0 | 1.77882364566392 |
| 13 | [3,3,3,3,5] | 3 | 5 | 2 | 80 | 12 | 0 | 2.15583737511565 |
| 14 | [3,4,5,4] | 3 | 4 | 5 | 20 | 30 | 12 | 2.23295050941568 |
| 15 | [4,6,8] | 4 | 6 | 8 | 12 | 8 | 6 | 2.31761091289276 |
| 16 | [5,6,6] | 5 | 6 | 2 | 12 | 20 | 0 | 2.47801865906759 |
| 17 | [3,10,10] | 3 | 10 | 2 | 20 | 12 | 0 | 2.96944901586341 |
| 18 | [4,6,10] | 4 | 6 | 10 | 30 | 20 | 12 | 3.80239449985117 |
| | [3,3,3,5] | 3 | 5 | 2 | 10 | 2 | 0 | 0.951056516295154 |
| | [4,4,5] | 4 | 5 | 2 | 5 | 2 | 0 | 0.986715155325985 |
以下が有効桁数確認のためにまとめた 20 桁 リストです。
Excel での有効桁数は 13 以上でした。
| | 名称 | 面積 | 体積 |
| 01 | [3,3,3] | 1.73205080756887 72935 | .117851130197757 92073 |
| 02 | [3,3,3,3] | 3.46410161513775 45871 | .471404520791031 68293 |
| 03 | [4,4,4] | 6.00000000000000 00000 | 1.00000000000000 00000 |
| 04 | [3,3,3,3,3] | 8.66025403784438 64676 | 2.18169499062491 23735 |
| 05 | [3,4,3,4] | 9.46410161513775 45871 | 2.35702260395515 84147 |
| 06 | [3,6,6] | 12.1243556529821 41055 | 2.71057599454843 21769 |
| 07 | [3,3,3,3,4] | 19.8564064605510 18348 | 7.88947739997539 02065 |
| 08 | [3,4,4,4] | 21.4641016151377 54587 | 8.71404520791031 68293 |
| 09 | [5,5,5] | 20.6457288070676 03073 | 7.66311896062463 19687 |
| 10 | [4,6,6] | 26.7846096908265 27522 | 11.3137084989847 60390 |
| 11 | [3,5,3,5] | 29.3059828449119 89541 | 13.8355259362494 04140 |
| 12 | [3,8,8] | 32.4346643636148 95173 | 13.5996632910744 43561 |
| 13 | [3,3,3,3,5] | 55.2867449584451 48944 | 37.6166499627333 62976 |
| 14 | [3,4,5,4] | 59.3059828449119 89541 | 41.6153237824979 67065 |
| 15 | [4,6,8] | 61.7551724393036 68108 | 41.7989898732233 30683 |
| 16 | [5,6,6] | 72.6072530341339 21879 | 55.2877307581227 39236 |
| 17 | [3,10,10] | 100.990760153101 98854 | 85.0396645593708 81555 |
| 18 | [4,6,10] | 174.292030342323 92088 | 206.803398874989 48482 |
| | [3,3,3,5] | 7.77108182010012 70793 | 1.57868932583326 32321 |
| | [4,4,5] | 8.44095480117793 38455 | 1.72047740058896 69228 |
双対多面体の 面積と 体積の Excel での計算式は お伝えする予定はまだありません。
面の形状は 1 種類 面芯寸 も 1 種類 なので
一つの面の 面積 × 総面数 が 双対多面体の 表面積 で
双対多面体の 表面積 × 面芯寸 ÷ 3 が 双対多面体の 体積 と
計算は 簡単そうですが
一つの面の 面積 のシンプルな計算式 が考えつかずにいます。
2015年5月29日
Excel 多面体 諸量
前回 Excel で 多面体諸量を求めました。
その値が どのくらいの精度で 計算できているのかを 調べるため
多倍長電卓LM というフリーウエアーを用いて計算した値と 比べてみました。
http://www.vector.co.jp/soft/win95/personal/se242555.html
以下に 多倍長電卓LM で得られた値のリストを載せておきます。
Excel で計算した値 の 有効桁数は 13 ぐらいでしょうか。
多倍長電卓LM は C言語的な ソフトなので 私には使いづらいですが
十進BASIC と同じくらい 大いに活用させてもらっています。
| 名称 | 基本数 | 稜芯寸 | 頂芯寸 |
| [3,3,3] | .577350269189625 76451 | .353553390593273 76220 | .612372435695794 52455 |
| [3,3,3,3] | .707106781186547 52440 | .500000000000000 00000 | .707106781186547 52440 |
| [4,4,4] | .816496580927726 03273 | .707106781186547 52440 | .866025403784438 64676 |
| [3,3,3,3,3] | .850650808352039 93218 | .809016994374947 42410 | .951056516295153 57212 |
| [3,4,3,4] | .866025403784438 64676 | .866025403784438 64676 | 1.00000000000000 00000 |
| [3,6,6] | .904534033733290 86794 | 1.06066017177982 12866 | 1.17260393995585 73886 |
| [3,3,3,3,4] | .928191377985571 60941 | 1.24722316799364 32518 | 1.34371337374460 17013 |
| [3,4,4,4] | .933948831094464 75958 | 1.30656296487637 65280 | 1.39896632596590 67020 |
| [5,5,5] | .934172358962715 69645 | 1.30901699437494 74242 | 1.40125853844407 35447 |
| [4,6,6] | .948683298050513 79960 | 1.50000000000000 00000 | 1.58113883008418 96660 |
| [3,5,3,5] | .951056516295153 57212 | 1.53884176858762 67014 | 1.61803398874989 48482 |
| [3,8,8] | .959682982260667 28914 | 1.70710678118654 75245 | 1.77882364566392 44509 |
| [3,3,3,3,5] | .972732850565595 86532 | 2.09705383525208 79925 | 2.15583737511563 97018 |
| [3,4,5,4] | .974607762378170 45237 | 2.17625089948282 15112 | 2.23295050941569 00495 |
| [4,6,8] | .976450976246513 24115 | 2.26303343845371 46237 | 2.31761091289276 65138 |
| [5,6,6] | .979432085486414 18658 | 2.42705098312484 22724 | 2.47801865906761 55376 |
| [3,10,10] | .985721919281301 91461 | 2.92705098312484 22724 | 2.96944901586339 84670 |
| [4,6,10] | .991316689541059 39137 | 3.76937712792171 66028 | 3.80239449985129 35848 |
| [3,3,3,5] | .850650808352039 93218 | .809016994374947 42410 | .951056516295153 57212 |
| [4,4,5] | .862103722396975 53031 | .850650808352039 93218 | .986715155325983 10732 |
2015年5月28日
<
1
2
3
4
5
6
7
8
9
10
11
12
13
>